|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Poisson stable positively 126.E
Poisson summation formula 192.C
Poisson summation formula (of Fourier transforms) 192.C
Poisson summation formula (on a locally compact Abelian group) 192.L
Poisson, Simeon Denis(1781-1840) 5.D 5.F 82.B 105.M 126.E 159.C 168.B 192.C 192.L 193.G 198.B 260.H 266 271.F 271.G 323.A 324.C 324.D 325.D 338.A 341.D 391.J 397.F 407.D App.A Tables 19.III
Polar (in projective geometry) 343.E
Polar (relative to pairing) 424.H
Polar (with respect to a conic) 78.J
Polar coordinates 90.C
Polar coordinates geodesic 90.C
Polar coordinates tangential 90.C
Polar decomposition 251.E
Polar element (a function element in the wider sense) 198.O
Polar element (of an integral element) 428.E
Polar form (of a complex number) 74.C
Polar plane (with respect to a quadric surface) 350.C
Polar set (in potential theory) 261.D 338.H
Polar space 191.I
Polar system (in projective geometry) 343.D
Polar tetrahedron 350.C
Polar tetrahedron self- 350.C
Polar triangle 78.J
Polar triangle self- 78.J
Polarity (with respect to a quadric hypersurface) 343.E
Polarization (on an Abelian variety) 3.G
Polarization electric 130.A
Polarization inhomogeneous 3.G
Polarization magnetic 130.A
Polarization principal 3.G
Polarized (Hodge structure) 16.V
Polarized (wave) 446
Polarized Abelian variety 3.G
Polarized Jacobian variety, canonically 3.G 9.E
Pole (of a complex function) 198.D
Pole (of a function on an algebraic curve) 9.C
Pole (of a function on an algebraic variety) 16.M
Pole (of a polar of a quadric hypersurface) 158.E
Pole (of a polar plane) 350.C
Pole (of a polar with respect to a conic) 78.J
Pole (of a roulette) 93.H
Pole divisor (of a function on an algebraic variety) 16.M
Pole north (of a complex sphere) 74.D
Pole north (of a sphere) 140
Pole Regge 132.C 386.C
Pole resonance 331.F
Pole south (of a complex sphere) 74.D
Pole south (of a sphere) 140
Pole, order of 198.D
Policy 127.A 405.C
Policy Markovian 405.C
Policy optimal 127.A
Polish space 22.I 273.J
Polit, Stephen H. 136.E
Polkinghorne, John Charlton(1930-) 146.r 386.C 386.r
Pollaczek, Felix(1892-1981) 145 307.C
Pollaczek—Geiringer, H. 298.r
Polonsky, Ivan P. 223.r 299.r
Polya type 374.J
Polya type, strictly of 374.J
Polya, George(1887-1985) 20.r 48.D 48.r 66.E 88.r 121.C 211.r 228.B 228.r 272.K 339.D 374.J 429.B
Polyakov, A.M. 80.r
Polya’s enumeration theorem 66.E
Polychromatic group 92.D
Polydisk 21.B
Polygamma functions 174.B App. Table
Polygon(s) 155.F
Polygon(s) Cauchy 316.C
Polygon(s) decomposition-equal 155.F
Polygon(s) force 19.C
Polygon(s) normal 234.C
Polygon(s) plane 155.F
Polygon(s) regular 357.A
Polygon(s) simple 155.F
Polygon(s) supplementation-equal 155.F
Polygonal number of order r 4.D
Polyharmonic 193.O
Polyhedral angle, regular 357.B
Polyhedral cone, convex 89.F
Polyhedral group, regular 151.G
Polyhedral, convex rational 16.Z
Polyhedron (polyhedra) (in an affine space) 7.D
Polyhedron (polyhedra) (of a simplicial complex) 65.A 70.C
Polyhedron (polyhedra) analytic 21.G
Polyhedron (polyhedra) convex 89.A
Polyhedron (polyhedra) corner 215.C
Polyhedron (polyhedra) Euclidean 70.B
Polyhedron (polyhedra) Euler theorem on 201.F
Polyhedron (polyhedra) integer 215.C
Polyhedron (polyhedra) regular 357.B
Polyhedron (polyhedra) topological 65.A
Polymatroid 66.F
Polynomial approximation 336
Polynomial approximation theorem (for  -functions) 58.E -functions) 58.E
Polynomial approximationbest (in the sense of Chebyshev) 336.H
Polynomial distribution App. A Table
Polynomial distribution negative App. A Table
Polynomial extrapolation method 303.F
Polynomial identity (on an algebra) 29.J
Polynomial representation (of GL(V)) 60.D
Polynomial ring 337.A 369
Polynomial ring of m variables 337.B
Polynomial time 71.B
Polynomial(s) 337
Polynomial(s) Alexander (of a knot) 235.C 235.D
Polynomial(s) alternating 337.I
Polynomial(s) associated Laguerre 317.D
Polynomial(s) Bernoulli 177.B
Polynomial(s) Bernshtein 336.A
Polynomial(s) Bernshtein (generalized) 418.H
Polynomial(s) characteristic (of a differential operator) 112.A 321.A
Polynomial(s) characteristic (of a linear mapping) 269.L
Polynomial(s) characteristic (of a matrix) 269.F
Polynomial(s) Chebyshev 317.D 336.H App. Table
Polynomial(s) Chebyshev orthogonal 19.G
Polynomial(s) cyclotomic 14.L
Polynomial(s) differential 113
Polynomial(s) Euler 177.C
Polynomial(s) Fourier-Hermite 176.I
Polynomial(s) Galois group of the 172.G
Polynomial(s) Gegenbauer 317.D 393.E App. Table
Polynomial(s) generalized trigonometric 18.B
Polynomial(s) Hermite 317.D
Polynomial(s) Hermite interpolation 223.E
Polynomial(s) Hilbert (of a graded R-module) 369.F
Polynomial(s) Hilbert (of a sheaf) 16.E
Polynomial(s) Hilbert (of an algebraic curve) 9.F
Polynomial(s) homogeneous of degree n 337.B
Polynomial(s) Hosokawa 235.D
Polynomial(s) in m variables 337.B
Polynomial(s) inseparable 337.G
Polynomial(s) irreducible 337.F
Polynomial(s) isobaric 32.C
Polynomial(s) Jacobi 317.D App. Table
Polynomial(s) Lagrange interpolation 223.A 336.G App. Table
Polynomial(s) Laguerre 317.D App. Table
Polynomial(s) Legendre 393.B App. Table
Polynomial(s) link 235.D
Polynomial(s) Lommel App. A Table
Polynomial(s) minimal (of a linear mapping) 269.L
Polynomial(s) minimal (of a matrix) 269.F
Polynomial(s) minimal (of an algebraic element) 149.E
Polynomial(s) monic 337.A
Polynomial(s) Neumann App. A Table
Polynomial(s) Newton interpolation 336.G
Polynomial(s) orthogonal 19.G App. Table
Polynomial(s) parity check 63.E
Polynomial(s) Poincare 201.B
Polynomial(s) primitive 337.D
Polynomial(s) reduced link 235.D
Polynomial(s) reducible 337.F
| Polynomial(s) ring of differential 113
Polynomial(s) Sato — Bernshtein 125.EE
Polynomial(s) Schlafli App. A Table
Polynomial(s) separable 337.G
Polynomial(s) simplest orthogonal 19.G
Polynomial(s) Snapper 16.E
Polynomial(s) Sonine 317.D App. Table
Polynomial(s) symmetric 337.I
Polynomial(s) system of orthogonal 317.D
Polynomial(s) trigonometric interpolation 336.E
Polynomial(s) ultraspherical 317.D
Polynomial(s) zonal 374.C
Polynomial(s), ring of 337.A 369
Polynomially transformable 71.E
Polytropic differential equation 291.F
Pomeranchuk theorem 386.B
Pomeranchuk, Isaak Yakovlevich(1913-1966) 386.B
Pommerenke, Christian(1933-) 48.r 77.F 169.F 438.r
Poncelet, Jean-Victor(1788-1867) 179.B 181 266 267
Pong, D.H. 345.A
Ponstein, J. 292.D
Pontryagin class(es) (of an 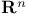 -bundle) 56.D -bundle) 56.D
Pontryagin class(es) combinatorial 56.H
Pontryagin class(es) of a manifold 56.F
Pontryagin class(es) rational 56.F
Pontryagin class(es) total 56.D
Pontryagin class(es) universal 56.D
Pontryagin duality theorem (on topological Abelian groups) 192.K 422.C
Pontryagin multiplication 203.D
Pontryagin number 56.F
Pontryagin product 203.D
Pontryagin pth power operation 64.B
Pontryagin, Lev Semenovich(1908-) 2.G 56.D 56.F 56.H 64 64.B 86.A 86.F 107.r 108.r 114.H 126.A 126.I 126.r 192.K 201.A 201.r 202.B 202.U 203.D 249.r 305.A 318.r 422.C 422.E 422.r 423.r
Ponzano, Giorgio Enrico(1939-) 146.A
Poor, Walter Andrew(1943-) 178.r
Popov ghost, Faddeev — 132.C 150.G
Popov, M.V. 291.E
Popov, Viktor Nikolaevich(1937-) 132.C 150.G
Popp, Herbert(1936-) 16.W
Population (in statistics) 397.B 401.E
Population characteristic 396.C
Population correlation coefficient 396.D
Population covariance 396.D
Population distribution 396.B 401.F
Population distribution hypothetical infinite 397.P
Population finite 373.A
Population infinite 401.E
Population kurtosis 396.C
Population mean 396.C
Population moment of order k 396.C
Population standard deviation 396.C
Population variance 396.C
Port network, M- 282.C
Port, Sidney Charles(1935-) 5.G
Port-admittance matrix 282.C
Port-impedance matrix 282.C
Porter 168.C
Porter, Alfred William(1863-1939) 116.r
Portrait, phase 126.B
Position general (complexes) 70.B
Position general (in a projective space) 343.B
Position general (of a PL mapping) 65.D
Position general, theorem 65.D
Position hyperboloid 350.D
Position method of false 301.C
Position representation 351.C
Position vector 442.A
Position vector (of a point of an aftine space) 7.A
Positive (chain complex) 200.C
Positive (class of vector bundles) 114.D
Positive (complex) 200.H
Positive (function on a C*-algebra) 308.D
Positive (functional on a C*-algebra) 36.G
Positive (Hermitian operation) 308.A
Positive (square matrix) 310.H
Positive boundary, open Riemann surface of 367.E
Positive completely (linear mapping between C*-algebras) 36.H
Positive cone, natural 308.K
Positive cycle (on an algebraic variety) 16.M
Positive definite (function) 192.B 192.J 394.C
Positive definite (Hermitian form) 348.F
Positive definite (matrix) 269.I
Positive definite (on a topological group) 36.L 437.B
Positive definite (potential) 338.D
Positive definite (sequence) 192.B
Positive definite kernel 217.H
Positive definite quadratic form 348.C
Positive direction (in a curvilinear integral) 198.B
Positive distribution 125.C
Positive divisor (of an algebraic curve) 9.C
Positive divisor (on a Riemann surface) 11.D
Positive element (in a lattice-ordered group) 243.G
Positive element (of an ordered field) 149.N
Positive element strictly 310.H
Positive element totally 14.G
Positive entropy, completely 136.E
Positive half-trajectory 126.D
Positive infinity 87.D 355.C
Positive kernel 217.H
Positive limit point 126.D
Positive matrix 269.N
Positive number 355.A
Positive operator (in vector lattices) 310.E
Positive orientation (of an oriented  -manifold) 105.F -manifold) 105.F
Positive orthant 89.G
Positive part (of an element of a vector lattice) 310.B
Positive prolongational limit set, first 126.D
Positive Radon measure 270.I
Positive real function 282.C
Positive recurrent ergodic class 260.B
Positive recurrent point 260.B
Positive root (of a semisimple Lie algebra) 248.M
Positive semidefinite (operator) 251.E
Positive semidefinite kernel 217.H
Positive semidefinite matrix 269.I
Positive semidefinite quadratic form 348.C
Positive semiorbit 126.D
Positive system, symmetric 112.S 326.D
Positive terms, series of 379.B
Positive type (function of) 192.B 192.J
Positive type (sequence of) 192.B
Positive type (symmetric kernel of) 338.D
Positive variation (of a mapping) 246.H
Positive variation (of a real bounded function) 166.B
Positive Weyl chamber 248.R
Positively invariant 126.D
Positively Lagrange stable 126.E
Positively Poisson stable 126.E
Positively regular process 44.C
Positivity O-S 150.F
Positivity reflection 1S0.F
Positivity T- 150.F
Possibility 411.L
Possible construction problem 179.A
Post problem 356.D
Post theorem 356.H
Post, Emil Leon(1897-1954) 31.B 75.D 97.r 161.B 240.D 356.A 365.D 365.H 365.r
Posterior density 401.B
Posterior distribution 398.B 401.B 403.G
Posterior risk 399.F
Postliminal C*-algebra 36.H
Postnikov complex 70.G
Postnikov system (of a CW complex) 148.D
Postnikov, Aleksei Georgievich(1921—) 295.E 328.* 328.r
Postnikov, Mikhail Mikhailovich(1927-) 70.G 148.D 172.r 305.A
Poston, Tim 51.r
Postulate(s) 35.A
Postulate(s) fifth (in Euclidean geometry) 139.A
Postulate(s) Nernst 419.A
Postulate(s) Peano 294.B
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -functions)
-functions) 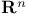 -bundle)
-bundle)  -manifold)
-manifold)