|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Separator 186.F
Sequence(s) 165.D
Sequence(s) (o)-convergent 87.L
Sequence(s) (o)-star convergent 87.L
Sequence(s) (R,S)-exact (of modules) 200.K
Sequence(s) admissible (in Steenrod algebra) 64.B App. Table
Sequence(s) asymptotic 30.A
Sequence(s) Blaschke 43.F
Sequence(s) Cauchy (in 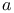 -adic topology) 284.B -adic topology) 284.B
Sequence(s) Cauchy (in a metric space) 273.J
Sequence(s) Cauchy (in a uniform space) 436.G
Sequence(s) Cauchy (of rational numbers) 294.E
Sequence(s) Cauchy (of real numbers) 355.B
Sequence(s) cohomology exact 201.L
Sequence(s) cohomology spectral 200.J
Sequence(s) connected, of functors 200.I
Sequence(s) convergent (of real numbers) 87.B 355.B
Sequence(s) divergent (of real numbers) 87.B
Sequence(s) double 379.E
Sequence(s) exact (of A-homomorphisms of A-modules) 277.E
Sequence(s) exact, of cohomology 200.F
Sequence(s) exact, of Ext 200.G
Sequence(s) exact, of homology 200.C
Sequence(s) exact, of Tor 200.D
Sequence(s) Farey 4.B
Sequence(s) Fibonacci 295.A
Sequence(s) finite 165.D
Sequence(s) fundamental (in a metric space) 273.J
Sequence(s) fundamental (in a uniform space) 436.G
Sequence(s) fundamental (of rational numbers) 294.E
Sequence(s) fundamental (of real numbers) 355.B
Sequence(s) fundamental, of cross cuts (in a simply connected domain) 333.B
Sequence(s) Gysin exact (of a fiber space) 148.E
Sequence(s) Hodge spectral 16.U
Sequence(s) homology exact (for simplicial complexes) 201.L
Sequence(s) homology exact (of a fiber space) 148.E
Sequence(s) homotopy exact 202.L
Sequence(s) homotopy exact (of a fiber space) 148.D
Sequence(s) homotopy exact (of a triad) 202.M
Sequence(s) homotopy exact (of a triple) 202.L
Sequence(s) independent, of partitions 136.E
Sequence(s) infinite 165.D
Sequence(s) interpolating 43.F
Sequence(s) Jordan — Hoelder (in a group) 190.G
Sequence(s) linear recurrent 295.A
Sequence(s) Mayer — Vietoris exact 201.C
Sequence(s) minimizing 46.E
Sequence(s) monotone (of real numbers) 87.B
Sequence(s) monotonically decreasing (of real numbers) 87.B
Sequence(s) monotonically increasing (of real numbers) 87.B
Sequence(s) normal (of open coverings) 425.R
Sequence(s) null (in 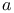 -adic topology) 284.B -adic topology) 284.B
Sequence(s) of Bernoulli trials 396.B
Sequence(s) of factor groups (of a normal chain) 190.G
Sequence(s) of functions 165.B 165.D
Sequence(s) of numbers 165.D
Sequence(s) of points 165.D
Sequence(s) of positive type 192.B
Sequence(s) of sets 165.D
Sequence(s) of Ulm factors (of an Abelian p-group) 2.D
Sequence(s) oscillating (of real numbers) 87.D
Sequence(s) pointwise convergent 435.B
Sequence(s) positive definite 192.B
Sequence(s) Puppe exact 202.G
Sequence(s) random 354.E
Sequence(s) rapidly decreasing 168.B
Sequence(s) recurrent, of order r 295.A
Sequence(s) reduced homology exact 201.F
Sequence(s) regular (of Lebesgue measurable sets) 380.D
Sequence(s) regular spectral 200.J
Sequence(s) relative Mayer — Vietoris exact 201.L
Sequence(s) short exact 200.I
Sequence(s) simply convergent 435.B
Sequence(s) slowly increasing 168.B
Sequence(s) spectral 200.J
Sequence(s) spectral (of singular cohomology of a fiber space) 148.E
Sequence(s) standard 400.K
Sequence(s) symbol (in the theory of microdifferential operators) 274.F
Sequence(s) uniformly convergent 435.A
Sequence(s) Wang exact (of a fiber space) 148.E
Sequencing problem, machine 376
Sequential decision function 398.F
Sequential decision problem 398.F
Sequential decision rule 398.F
Sequential probability ratio test 400.L
Sequential sampling inspection 404.C
Sequential space 425.CC
Sequential test 400.L
Sequentially compact (space) 425.S
Seregin, L.V. 115.r
Sergner, J.A. 19.B
Serial correlation coefficient 397.N 421.B
Serial cross correlation coefficient 397.N
Series 379 App. Table
Series  - (of a group) 151.F - (of a group) 151.F
Series absolutely convergent 379.C
Series absolutely convergent double 379.E
Series allied (of a trigonometric series) 159.A
Series alternating 379.C
Series ascending central (of a Lie algebra) 248.C
Series asymptotic 30
Series asymptotic power 30.A
Series binomial App. A Table
Series binomial coefficient 121.E
Series characteristic (in a group) 190.G
Series commutatively convergent 379.C
Series complementary (of unitary representations of a complex semisimple Lie group) 437.W
Series complementary degenerate (of unitary representations of a complex semisimple Lie group) 437.W
Series composition (in a group) 190.G
Series composition (in a lattice) 243.F
Series composition factor (of a composition series in a group) 190.G
Series conditionally convergent 379.C
Series conditionally convergent double 379.E
Series conjugate (of a trigonometric series) 159.A
Series convergent 379.A
Series convergent double 379.E
Series convergent power 370.B
Series convergent power, ring 370.B
Series degenerate (of unitary representations of a complex semisimple Lie group) 437.W
Series derived (of Lie algebra) 248.C
Series descending central (of a Lie algebra) 248.C
Series Dini 39.D
Series Dirichlet 121
Series Dirichlet, of the type  121.A 121.A
Series discrete (of unitary representations of a semisimple Lie group) 437.X
Series divergent 379.A
Series divergent double 379.E
Series double 379.E
Series Eisenstein 32.C
Series Eisenstein — Poincare 32.F
Series exponential 131.D
Series factorial 104.F 121.E
Series field of formal power, in one variable 370.A
Series finite 379.A App. Table
Series formal power 370.A
Series formal power, field in one variable 370.A
Series formal power, ring 370.A
Series Fourier 159 197.C App. Table
Series Fourier (of a distribution) 125.P
Series Fourier (of an almost periodic function) 18.B
Series Fourier cosine App. A Table
Series Fourier sine App. A Table
Series Fourier — Bessel 39.D
Series Gauss 206.A
Series generalized Eisenstein 450.T
Series generalized Schloemilch 39.D
Series generalized trigonometric 18.B
Series geometric 379.B App. Table
Series Heine 206.C
Series hypergeometric 206.A
| Series infinite 379.A App. Table
Series iterated, by columns (of a double series) 379.E
Series iterated, by rows (of a double series) 379.E
Series Kapteyn 39.D App. Table
Series Lambert 339.C
Series Laurent 339.A
Series logarithmic 131.D
Series lower central (of a group) 190.J
Series majorant 316.G
Series majorant (of a sequence of functions) 435.A
Series Neumann 217.D
Series of nonnegative terms 379.B
Series of positive terms 379.B
Series ordinary Dirichlet 121.A
Series orthogonal (of functions) 317.A
Series oscillating 379.A
Series Poincare 32.B
Series power 21.B 339 370.A App. Table
Series power (in a complete ring) 370.A
Series power, ring 370.A
Series power, with center at the point at infinity 339.A
Series principal (in an  -group) 190.G -group) 190.G
Series principal (of unitary representations of a complex semisimple Lie group) 258.C 437.W
Series principal (of unitary representations of a real semisimple Lie group) 258.C 437.X
Series principal H- 437.X
Series properly divergent 379.A
Series Puiseux 339.A
Series repeated, by columns (of a double series) 379.E
Series repeated, by rows (of a double series) 379.E
Series ring of convergent power 370.B
Series ring of formal power 370.A
Series ring of power 370.A
Series Schloemilch 39.D App. Table
Series simple 379.E
Series singular 4.D
Series supplementary 258.C
Series Taylor 339.A
Series termwise integrable 216.B
Series theta 348.L
Series theta-Fuchsian, of Poincare 32.B
Series time 397.A 421.A
Series trigonometric 159.A
Series unconditionally convergent 379.C
Series uniformly absolutely convergent 435.A
Series upper central (of a group) 190.J
Serre 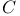 -theory 202.N -theory 202.N
Serre conjecture 369.F
Serre duality theorem (on complex manifolds) 72.E
Serre duality theorem (on projective varieties) 16.E
Serre formulas, Frenet- (on curves) 111.D App. Table
Serre theorem (for ample line bundles) 16.E
Serre, Jean-Pierre(1926-) 3.N 3.r 9.r 12.B 13.r 15.E 16.C 16.E 16.T 16.r 20 21.L 21.Q 29.r 32.D 52.N 59.H 59.r 64.B 64.r 70.r 72.E 72.K 72.r 122.F 147.K 147.O 148.A 172.r 200.K 200.M 200.r 202.N 202.U 202.r 237.J 248.r 249.r 257.r 284.G 362.r 366.D 369.F 369.r 426 428.G 450.G 450.J 450.R 450.r
Serret, Joseph Alfred(1819-1885) 111.D 238.r App.A Table
Serrin, James Burton(1926-) 275.A 275.D 323.D 323.E
Servais, C 297.D
Seshadri, Conjeeveram Srirangachari(1932-) 16.Y 16.r
Seshu, Sundaram(1926-) 282.r
Sesquilinear form (on a linear space) 256.Q
Sesquilinear form (on a product of two linear spaces) 256.Q
Sesquilinear form nondegenerate 256.Q
Sesquilinear form, matrix of 256.Q
Set function(s) 380
Set function(s)  -absolutely continuous additive 380.C -absolutely continuous additive 380.C
Set function(s)  -singular additive 380.C -singular additive 380.C
Set function(s) additive 380.C
Set function(s) completely additive 380.C
Set function(s) finitely additive 380.B
Set function(s) monotone decreasing 380.B
Set function(s) monotone increasing 380.B
Set function(s) of bounded variation 380.B
Set theory 381.F
Set theory axiomatic 33 156.E
Set theory Bernays — Goedel 33.A 33.C
Set theory Boolean-valued 33.E
Set theory classical descriptive 356.H
Set theory effective descriptive 356.H
Set theory general 33.B
Set theory Goedel 33.C
Set theory Zermelo 33.B
Set theory Zermelo — Fraenkel 33.A 33.B
Set(s) 381
Set(s) 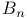 22.D 22.D
Set(s) 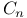 22.D 22.D
Set(s) 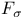 270.C 270.C
Set(s) 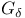 270.C 270.C
Set(s) 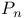 22.D 22.D
Set(s)  -limit 126.D -limit 126.D
Set(s) 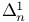 22.D 22.D
Set(s) 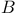 -measurable 270.C -measurable 270.C
Set(s)  -measurable 270.D -measurable 270.D
Set(s)  -null 270.D -null 270.D
Set(s)  -limit 126.D -limit 126.D
Set(s) 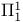 22.A 22.A
Set(s) 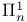 22.D 22.D
Set(s)  - 308.I - 308.I
Set(s) 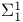 22.A 22.A
Set(s) 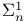 22.D 22.D
Set(s) (general) recursive 97
Set(s) A- 22.A 409.A
Set(s) absolutely convex (in a linear topological space) 424.E
Set(s) analytic 22.A 22.I
Set(s) analytic (in the theory of analytic spaces) 23.B
Set(s) analytic wave front 274.D
Set(s) analytically thin (in an analytic space) 23.D
Set(s) arbitrary 381.G
Set(s) asymptotic 62.A
Set(s) asymptotic ratio 308.I
Set(s) axiom of power 33.B 381.G
Set(s) Baire 126.H 270.C
Set(s) bargaining 173.D
Set(s) basic (for an Axiom A flow) 126.J
Set(s) basic (of a structure) 409.B
Set(s) basic open 425.F
Set(s) bifurcation 51.F 418.F
Set(s) border 425.N
Set(s) Borel (in a Euclidean space) 270.C
Set(s) Borel (in a topological space) 270.C
Set(s) Borel in the strict sense 270.C
Set(s) boundary 425.N
Set(s) boundary cluster 62.A
Set(s) bounded (in a locally convex space) 424.F
Set(s) bounded (in a metric space) 273.B
Set(s) bounded (in an affine space) 7.D
Set(s) CA 22.A
Set(s) Cantor 79.D
Set(s) catastrophe 51.F
Set(s) chain recurrent 126.E
Set(s) characteristic (of a partial differential operator) 320.B
Set(s) characteristic (of an algebraic family on a generic component) 15.F
Set(s) choice 34.A
Set(s) closed 425.B
Set(s) cluster 62.A
Set(s) coanalytic 22.A
Set(s) compact (in a metric space) 273.F
Set(s) compact (in a topological space) 425.S
Set(s) complementary 381.B
Set(s) complementary analytic 22.A
Set(s) complete 241.B
Set(s) complete orthonormal (of a Hilbert space) 197.C
Set(s) connected 79.A
Set(s) constraint (of a minimization problem) 292.A
Set(s) convex 7.D 89
Set(s) countably equivalent (under a nonsingular bimeasurable transformation) 136.C
Set(s) curvilinear cluster 62.C
Set(s) cylinder 270.H
Set(s) dense 425.N
Set(s) dependent 66.G
Set(s) derived 425.O
Set(s) determining (of a domain in  ) 21.C ) 21.C
Set(s) difference (of blocks) 102.E
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



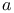 -adic topology)
-adic topology) - (of a group)
- (of a group) 
 -group)
-group) 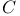 -theory
-theory  -absolutely continuous additive
-absolutely continuous additive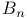
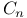
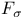
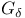
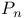
 -limit
-limit 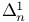
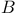 -measurable
-measurable  -limit
-limit 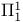
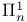
 -
- 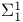
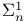
 )
)