|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Representation(s) double-valued 258.B
Representation(s) dual 362.E
Representation(s) equivalent 362.C
Representation(s) factor (of a topological group) 437.E
Representation(s) factor, of type I, II, or III 308.M 437.E
Representation(s) faithful 362.B
Representation(s) Fock 150.C
Representation(s) Gel’fand (of a commutative Banach algebra) 36.E
Representation(s) generalized canonical (of Gaussian processes) 176.E
Representation(s) generating (of a compact Lie group) 249.U
Representation(s) half-spin (even, odd) 61.E
Representation(s) Herglotz’s integral 43.I
Representation(s) in terms of arc length (of a continuous arc) 246.A
Representation(s) induced 362.G
Representation(s) induced (of a finite group) 362.G
Representation(s) induced (of a unitary representation of a subgroup) 437.O
Representation(s) integral (of a group) 362.G 362.K
Representation(s) integral, Cauchy’s 21.C
Representation(s) irreducible (of a Banach algebra) 36.D
Representation(s) irreducible (of an algebra or a group) 362.C
Representation(s) irreducible projective 362.J
Representation(s) isomorphic 362.C
Representation(s) isotropy 431.C
Representation(s) Kaellen — Lehmann 150.D
Representation(s) kernel (of a Green’s operator) 189.B
Representation(s) l-adic 3.E
Representation(s) Lax 287.B 287.C 387.C
Representation(s) left regular (of a group) 362.B
Representation(s) list 186.D
Representation(s) Mandelstam 132.C
Representation(s) matrix 362.D
Representation(s) modular (of a finite group) 362.G
Representation(s) momentum 351.C
Representation(s) normal (of a von Neumann algebra) 308.C
Representation(s) ordinary (of a finite group) 362.G
Representation(s) parametric 165.C
Representation(s) parametric (of a subspace of an affine space) 7.C
Representation(s) parametric (of Feynman integrals) 146.B
Representation(s) permutation (of a group) 362.B
Representation(s) permutation, reciprocal (of a group) 362.B
Representation(s) polynomial (of GL(V)) 60.D
Representation(s) position 351.C
Representation(s) projective (of a group) 362.J
Representation(s) projective, irreducible 362.J
Representation(s) quotient (of a linear representation) 362.C
Representation(s) rational (of a matrix group) 226.B
Representation(s) rational (of GL(V)) 60.D
Representation(s) real (of a Lie group) 349.O
Representation(s) reciprocal linear (of an algebra) 362.C
Representation(s) reciprocal permutation (of a group) 362.B
Representation(s) reduced (of an algebra) 362.E
Representation(s) reducible 362.C
Representation(s) regular (of a locally compact group) 69.B
Representation(s) regular (of a topological transformation group) 437.A
Representation(s) regular, left (of a group) 362.B
Representation(s) regular, left (of an algebra) 362.C
Representation(s) regular, right (of a group) 362.B
Representation(s) regular, right (of an algebra) 362.E
Representation(s) Schroedinger 351.C
Representation(s) semisimple 362.C
Representation(s) similar 362.C
Representation(s) similar matrix (semilinear mapping) 256.D
Representation(s) similar projective 362.J
Representation(s) simple 362.C
Representation(s) slice 431.C
Representation(s) special (of a Jordan algebra) 231.C
Representation(s) spectral 390.E
Representation(s) spherical (of a differentiable manifold) 111.G
Representation(s) spherical (of a space curve) 111.F
Representation(s) spherical (of a unimodular locally compact group) 437.Z
Representation(s) spin 61.E
Representation(s) spin (of SO(n)) 60.J
Representation(s) spinor, of rank 258.B
Representation(s) strongly continuous (of a topological group) 69.B
Representation(s) sub- 362.C
Representation(s) sub- (of a projective representation) 362.J
Representation(s) tensor (of a general linear group) 256.M
Representation(s) translation, theorem 375.H
Representation(s) transposed 362.E
Representation(s) tree 96.D
Representation(s) unit (of a group) 362.C
Representation(s) vector (of a Clifford group) 61.D
Representation(s) weakly continuous (of a topological group) 69.B
Representation(s) without multiplicity 437.G
Representation(s) zero (of an algebra) 362.C
Representation(s), module of 69.D
Representation(s), tensor product of 362.C
Representative (of an equivalence class) 135.B
Representative function (of a compact Lie group) 249.U
Representative ring (of a compact Lie group) 249.U
Representing function (of a predicate) 356.B
Representing function (of a subset) 381.C
Representing measure 164.C
Reproducing kernel 188.G
Reproducing property (of a probability distribution) 341.E App. Table
Reproduction function 263.A
Requirements, variational principles with relaxed continuity 271.G
Reseboom, J.H. 376.r
Reserve, liability 214.B
Residual (subset of a directed set) 311.D
Residual limit set 234.E
Residual set 126.H 425.N
Residual spectrum 390.A
Residue (class) algebra 29.A
Residue (class) field 149.C 368.F 439.B
Residue (class) ring (modulo an ideal) 368.F
Residue character 295.D
Residue class (modulo an ideal in a ring) 368.F
Residue system modulo m complete 297.G
Residue system modulo m reduced 297.G
Residue theorem 198.E
Residue theorem (on a nonsingular curve) 9.E
Residue(s) (of a complex function) 198.E
Residue(s) norm- (modulo 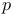 ) 14.P ) 14.P
Residue(s) norm- (symbol) 14.Q 257.F
Residue(s) of the nth power (modulo 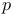 ) 14.M ) 14.M
Residue(s) power- (symbol) 14.N
Residue(s) quadratic 297.H
Residue(s), calculus of 198.F
Resistance, negative 318.B
Resistance, specific 130.B
Resnikoff, George Joseph(1915 ) STR
Resolution 200.H
Resolution 2l 102.I
Resolution 2l+1 102.I
Resolution complete free (of Z) 200.N
Resolution complex spectral 390.E
Resolution flabby 125.W
Resolution injective (in an Abelian category) 200.I
Resolution of singularities 16.L
Resolution of singularities (of an analytic space) 23.D 418.B
Resolution of the identity 390.D
Resolution right (of an A-module) 200.F
Resolution right injective (of an A-module) 200.F
Resolution spectral 390.E
Resolution standard (of Z) 200.M
Resolutionminimal 418.C
Resolutionprojective (in an Abelian category) 200.I
Resolutive 207.B
Resolutive compactification 207.B
Resolvent (of a kernel) 217.D
Resolvent (of a linear operator) 251.F
Resolvent (operator of a Markov process) 261.D
Resolvent convergence norm 331.C
Resolvent convergence strong 331.C
Resolvent cubic App. A Table
Resolvent equation 251.F
Resolvent set (of a linear operator) 251.F 390.A
Resonance model, dual 132.C
Resonance pole 331.F
| Resonance theorem 37.H
Response 405.A
Response surface 102.M
Response surface designs for exploring 102.M
Rest energy 359.C
Rest point (of a trajectory) 126.D
Restitutive force 318.B
Restricted (Lorentz group) 258.A
Restricted Burnside problem (in group theory) 161.C
Restricted differential system 191.I
Restricted direct product 6.B
Restricted direct product (of an infinite number of groups) 190.L
Restricted direct product (of locally compact groups) 6.B
Restricted holonomy group 80.D 364.E
Restricted homogeneous holonomy group 364.E
Restricted homotopy 202.B
Restricted Lie algebra 248.V
Restricted minimal condition (in a commutative ring) 284.A
Restricted quantifier 33.B
Restricted three-body problem 420.F
Restriction (in a presheaf) 383.A
Restriction (of a connection) 80.F
Restriction (of a continuous flow) 126.D
Restriction (of a distribution) 125.D
Restriction (of a mapping) 381.C
Restriction crystallographic 92.A
Restriction scalar (of a B-module) 277.L
Restriction unitary (of a semisimple Lie algebra) 248.P
Resultant(s) 369.E
Resultant(s) system of 369.E
Retardation 163.A
Retarded differential equation 163.A
Retarded type (functional differential equation) 163.A
retract 202.D
Retract absolute 202.D
Retract absolute neighborhood 202.D
Retract deformation 202.D
Retract fundamental 382.C
Retract fundamental absolute (FAR) 382.C
Retract fundamental absolute neighborhood (FANR) 382.C
Retract neighborhood 202.D
Retract neighborhood deformation 202.D
Retract strong deformation 202.D
Retraction 202.D
Retrieval, information (system) 96.F
Retrospective study 40.E
RETURN 127.C
Return maximum 127.B
Returnfirst- (mapping, map) 126.C
Reuleaux triangle 89.E 111.E
Reuleaux, Franz(1829-1905) 89.E 111.E
Reversal, time 258.A
Reversed process 261.F
Review technique, program evaluation and 376
Revolution, ellipsoid of 350.B
Revolution, elliptic paraboloid of 350.B
Revolution, hyperboloid of, of one sheet 350.B
Revolution, hyperboloid of, of two sheets 350.B
Revolution, surface of 111.I
Revuz, Daniel Robert(1936-) 260.J 261.E
Reynolds law of similarity 205.C
Reynolds number 116.B 205.C
Reynolds number, magnetic 259
Reynolds, Osborne(1842-1912) 116.B 205.C 259
Rhaeticus, Georg Joachim(1514-1574) 432.C
Rheinboldt, Werner Carl(1927-) 301.r
Rhodes, John L.(1937-) 31.r
Ribenboim, Paulo(1928-) 145.r
Ribet, Kenneth A. 14.L 450.J 450.r
Riccati differential equation App. A Table
Riccati differential equation generalized App. A Table
Riccati differential equation matrix 86.E
Riccati equation, matrix 405.G
Riccati, Jacopo Francesco(1676-1754) 86.E 107.A 405.G App.A Table
Ricci curvature 364.D
Ricci equation 365.C
Ricci formula 417.B App. Table
Ricci tensor 364.D 417.B App. Table
Ricci, Curbastro Gregorio(1853-1925) 109 364.D 365.C 417.B 417.F App.A Table
Ricci, Matteo(1552-1610) 57.C
Rice, John Richard(1934-) 299.r 336.r
Richard paradox 319.B
Richard, Jules Antoine(1862-1956) 319.B
Richardson method 302.C
Richardson, C H. 104.r
Richardson, Lewis Fry(1881-1953) 302.C 304.E
Richardson, Roger Wolcott Jr.(1930-) 431.r
Richert, Hans-Egon(1924-) 4.C 123.D 123.E 123.r
Richter, Hans(1912-1978) 443.A
Richter, Wayne H.(1936-) 81.D 81.r
Richtmyer, Robert Davis(1910 ) 304.r
Rickart, Charles Earl(1913-) 36.r 231.r 443.A
Rickman, Seppo U.(1935-) 352.F
Rieffel, Marc A.(1937-) 308.H 443.H
Riemann  function 3.L function 3.L
Riemann  function 450.V function 450.V
Riemann (differential) equation, Cauchy (for a holomorphic function of several complex variables) 21.C
Riemann (differential) equation, Cauchy (for a holomorphic function of two complex variables) 320.F
Riemann (differential) equation, Cauchy — 198.A 274.G
Riemann bilinear relations, Hodge — 16.V
Riemann continuation theorem 21.F
Riemann differential equation App. A. Table 18.I
Riemann function (of a Cauchy problem) 325.D
Riemann hypothesis 450.A 450.I 450.P 450.Q
Riemann integrable (function) 216.A
Riemann integral 37.K 216.A
Riemann lower integral 216.A
Riemann mapping theorem 77.B
Riemann matrix 3.I
Riemann method of summation 379.S
Riemann non-Euclidean geometry 285.A
Riemann P-function App. A Tables 18.I
Riemann period inequality 3.L
Riemann period relation 3.L
Riemann problem 253.D
Riemann sphere 74.D
Riemann structure, Cauchy — 344.A
Riemann sum 216.A
Riemann surface(s) 367
Riemann surface(s) abstract 367.A
Riemann surface(s) closed 367.A
Riemann surface(s) elliptic 367.D
Riemann surface(s) hyperbolic 367.D
Riemann surface(s) maximal 367.F
Riemann surface(s) open 367.A
Riemann surface(s) open, of null boundary 367.E
Riemann surface(s) open, of positive boundary 367.E
Riemann surface(s) parabolic 367.D
Riemann surface(s) prolongable 367.F
Riemann surface(s), classification theory of 367.E
Riemann theorem (on removable singularities) 198.D
Riemann theorem (on series with real terms) 379.C
Riemann upper integral 216.A
Riemann — Hilbert problem (for integral equations) 217.J
Riemann — Hilbert problem (for linear ordinary differential equations) 253.D
Riemann — Hurwitz formula (on coverings of a nonsingular curve) 9.I
Riemann — Hurwitz relation 367.B
Riemann — Lebesgue theorem 159.A 160.A
Riemann — Roch group 366.D
Riemann — Roch inequality (on algebraic surfaces) 15.D
Riemann — Roch theorem(s) 366
Riemann — Roch theorem(s) (for compact complex surface) 366.C
Riemann — Roch theorem(s) (on algebraic surfaces) 15.D
Riemann — Roch theorem(s) (on nonsingular algebraic curves) 9.C
Riemann — Roch theorem(s) (on Riemann surfaces) 11.D
Riemann — Roch theorem(s) for a line bundle 366.C
Riemann — Roch theorem(s) for an adjoint system 15.D
Riemann — Roch theorem(s) for differentiable manifolds 237.G
Riemann — Roch theorem(s) generalized (on algebraic curves) 9.F
Riemann — Roch type, Grothendieck theorem of 366.D
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



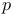 )
)  function
function  function
function