|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Sapiro see Shapiro
Sapronov, Yu.I. 286.r
Sarason, Donald Erik(1933-) 164.K 164.r
Sard theorem 105.J 208.B
Sard — Smale theorem 286.P
Sard, Arthur(1909-1980) 105.J 208.B 286.P
Sargsyan(Sargsjan), L.S. 315.r
Sarhan, Ahmed E. 374.r
Saribekovich, Sargsyan Iskhan(1931-) 315.r
Sario, Leo Reino(1916-) 48.r 77.E 77.r 124.C 124.r 169.r 207.r 367.E 367.G 367.r
Sarton, George Alfred Leon(1884-1956) 26.r 209.r 372.r
Sasaki — Nitsche formula, Gauss — Bonnet — 275.C
Sasaki, Shigeo(1912-) 110.E 275.C 365.J
Sasakian manifold 110.E
Sasieni, Maurice W. 307.r
Sataev, E.A. 136.F 136.r
Satake diagram App. A Table
Satake diagram (of a compact symmetric Riemannian space) 437.AA
Satake diagram (of a real semisimple Lie algebra) 248.U
Satake, Ichiro(1927-) 13.r 16.Z 21.Q 32.F 59.H 122.r 248.U 248.r 384.r 437.AA
Satellite left 200.I
Satellite right 200.I
Satisfiability, problem of (of a proposition) 97
Satisfiable (formula) 276.C
Sato conjecture 450.S
Sato — Bernshtein polynomial 125.EE
Sato, Atsushi(1954-) 154.H
Sato, Fumihiro(1949-) 450.V
Sato, Ken-iti(1934-) 115.C 115.D 263.r
Sato, Mikio(1928-) 20 112.D 125.A 125.V 125.W 125.BB 125.EE 146.A 146.C 162.* 162.r 274.I 345.B 386.C 387.C 418.H 450.A 450.M 450.Q 450.S 450.V
Sato, Tokui(1906-1983) 217.r 288.B
Sattinger, David H. 126.M 286.r
Saturated ((B,N)-pair) 151.J
Saturated (fractional factorial design) 102.I
Saturated model, k- 293.B
Savage theorem, Girshick — 399.F
Savage zero-one law, Hewitt — 342.G
Savage, I.Richard(1925-) 371.A 371.C 371.r
Savage, John E. 71.r
Savage, Leonard Jimmie(1917-1971) 342.G 399.F 399.r 401.B 401.F
Savings premium 214.B
Sawada, Ken(1953-) 126.J
Sawashima, Ikuko(1929-) 310.H
Saxer, Walter(1896-1974) 214.r
Sazonov topology 341J
Sazonov, Vyachcslav Vasil’evich(1935-) 341.J
Scalar change (of a B-module) 277.L
Scalar curvature 364.D App. Table
Scalar extension (of a linear representation) 362.F
Scalar extension (of an A -module) 277.L
Scalar extension (of an algebra) 29.A
Scalar field 105.O
Scalar field (in a 3-dimensional Euclidean space) 442.D
Scalar field free 377.C
Scalar integral 443.F 443.I
Scalar matrix 269.A
Scalar multiple (in a linear space) 256.A
Scalar multiple (of a linear operator) 37.C
Scalar multiple (of a vector) 442.A
Scalar multiple (of an element of a module) 277.D
Scalar multiplication (in a module) 277.D
Scalar multiplication (on vectors) 442.A
Scalar operator 390.K
Scalar potential 130.A 442.D
Scalar product 442.B App. Table
Scalar restriction (of a B-module) 277.L
Scalar sum (of linear operators) 37.C
Scalar triple product 442.C
Scalar(s) (in a linear space) 256.A 256.J
Scalar(s) (of a module over a ring) 277.D
Scalar(s), field of (of a linear space) 256.A
Scalar(s), ring of (of a module) 277.D
Scalarly integrable 443.F 443.I
Scalarly measurable 443.B 443.I
Scale canonical 115.B
Scale matrix 374.C
Scale natural 260.G
Scale of Banach space 286.Z
Scale ordinal 397.M
Scale parameter 396.I 400.E
Scale two-sided 19.D
Scaled, 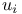 - 19.D - 19.D
Scaling method 346.E
Scaling, metric multidimensional 346.E
Scaling, multidimensional 346.E
Scarf, Herbert Ely(1930-) 173.E 227.r
Scatter diagram 397.H
Scattered (sheaf) 383.E
Scattered set 425.O
Scattered zeros, function with 208.C
Scattering 375.A
Scattering amplitude 375.C 386.B
Scattering amplitude partial wave 375.E
Scattering cross section 375.A
Scattering data 387.D
Scattering elastic 375.A
Scattering inelastic 375.A
Scattering operator 375.B 375.F 375.H
Scattering state 375.B
Scattering state, completeness of the 150.D
Scattering theory, Haag — Ruelle 150.D
Scegol’kov see Shchegol’kov
Schaaf, Manfred 258.r
Schade, J.P. 95.r
Schaefer, Helmut(1925-) 217.r 310.A 310.H
Schaeffer, Albert Charles(1907-) 438.B 483.C
Schaefke, Friedrich Wilhelm(1922-) 268.r 389.r
Schafheitlin formula, Sonine — App. A Table
Schafheitlin, Paul(1861-) App.A Table
Schaible, Siegfried 264.r
Schapira, Pierre M.(1943-) 112.D 125.Y 162
Schark, I.J. 164.I
Schatten, Robert(1911-1977) 68.I
Schauder basis 37.L
Schauder degree, Leray — 286.D
Schauder estimate 323.C
Schauder fixed-point theorem 153.D 286.D
Schauder fixed-point theorem Leray — 286.D 323.D
Schauder theorem, Riesz — 68.E
Schauder, Juliusz Pawel(1899-1943) 37.L 68.E 153.D 286.D 323.C 323.D 323.r 325.C 325.r
Schechter, Martin(1930-) 112.F 112.H 189.B 320.r 323.H
Scheduling 376
Scheduling and production planning 376
Scheduling job-shop 307.C
Scheduling model 307.C
Scheduling network 307.C
Scheduling problem flow-shop 376
Scheduling problem job-shop 376
Scheduling problem machine 376
Scheduling problem multiprocessor 376
Scheffe model 346.C
Scheffe theorem, Lehmann — 399.C
Scheffe, Henry(1907-1977) 102.r 346.C 399.C 399.r
Scheffers, Georg(1866-1945) 247.r
Scheifele, Gerhard 55.r
Scheinberg, Stephen 164.K
Scheja theorem 21.M
Scheja, Giinter(1932-) 21.M 21.r
Schema of Souslin 22.B
Scheme 16.D
Scheme adaptive 299.C
Scheme affine 16.D
Scheme Aitken’s interpolation 223.B
Scheme algebraic 16.D
Scheme automatic integration 299.C
Scheme coarse moduli 16.W
Scheme complete 16.D
Scheme consistent-mass 304.D
Scheme deformation of X over a connected 16.W
Scheme difference 304.E
| Scheme difference, of backward type 304.F
Scheme difference, of forward type 304.F
Scheme explicit 304.F
Scheme fine moduli 16.W
Scheme formal 16.X
Scheme Friedrichs 304.F
Scheme group 16.H
Scheme Hilbert 16.S
Scheme implicit 304.F
Scheme integral 16.D
Scheme inverted filing 96.F
Scheme irreducible 16.D
Scheme K-complete 16.D
Scheme Lax — Wendroff 304.F
Scheme locally Noetherian formal 16.X
Scheme moduli 16.W
Scheme Noetherian 16.D
Scheme nonadaptive 299.C
Scheme Over S 16.D
Scheme Picard 16.P
Scheme projective 16.E
Scheme quasiprojective 16.E
Scheme S- 16.D
Scheme separated 16.D
Scheme separated formal 16.X
Scheme, morphism of 16.D
Scherk, Heinrich Ferdinand 275.A
Scherk, John(1947-) 132.r
Scherk, Peter(1910-1985) 4.A
Scherk’s surface 275.A
Schetzen, Martin 95.r
Schickard, Wilhelm(1592-1635) 75.A
Schiffer, Menahem Max(1911-) 77.E 77.r 188.r 367.r 438.B 438.C
Schiffman, M. 275.B
Schilling, Otto Franz Georg(1911-1973) 257.r 439.r
Schlaefli diagram (of a complex semisimple Lie algebra) 248.S
Schlaefli formula App. A Table
Schlaefli integral representation 393.B
Schlaefli polynomial App. A Table
Schlafli, Ludwig(1814-1895) 105.A 248.S 393.B App.A Tables IV
Schlaifer, Robert 398.r
Schlesinger equations 253.E
Schlesinger, Ludwig(1864-1933) 253.E 253.r
Schlessinger, Michael 16.r
Schlicht 438.A
Schlicht Bloch constant 77.F
Schlichtartig 367.G
Schlichting, Hermann(1907-) 205.r 433.A
Schlieder theorem, Reeh — 150.E
Schlieder, Siegfried(1918-) 150.E
Schloemilch criterion App. A Table
Schloemilch remainder, Roche — App. A Table
Schloemilch series 39.D App. Table
Schloemilch series generalized 39.D
Schlomilch, Otto 39.D App.A Tables 10.II 19.III
Schmeidler, David 173.D
Schmetterer, Leopold(1919-) 399.N
Schmid, Hermann Ludwig(1908-1956) 59.H
Schmid, Wilfried(1943-) 16.r 437.W
Schmidt class, Hilbert — 68.I
Schmidt condition 379.M
Schmidt expansion theorem, Hilbert — 217.H
Schmidt norm, Hilbert — 68.I
Schmidt orthogonalization 317.A
Schmidt orthogonalization Gram — 317.A
Schmidt procedure, Lyapunov — 286.V
Schmidt theorem 118.D
Schmidt theorem, Knopp — 208.C
Schmidt theorem, Krull — Remak — (in group theory) 190.L
Schmidt type, integral operator of Hilbert — 68.C
Schmidt type, kernel of Hilbert — 217.I
Schmidt, Erhald(1876-1959) 68.C 68.I 139.G 217.H 217.I 286.V 302.E 317.A 445
Schmidt, Friedrich Karl(1901-1977) 12.B 59.G 450.P
Schmidt, O.Y. see Shmidt
Schmidt, Robert(1898-1964) 208.C 379.M
Schmidt, Wolfgang M.(1933-) 83.r 118.B 118.D 118.r 182.G 182.r 354.r 430.C 437.W
Schnee theorem, Knopp — (on method of summation) 379.M
Schnee, Walter 379.M
Schneider, Michael(1942-) 16.r
Schneider, Theodor(1911-) 182.r 196 430.A 430.B 430.r
Schober, Glenn E.(1938-) 438.r
Schoen, Richard M.(1950-) 275.D 275.F 364.r
Schoenberg, Isaac Jacob(1903-) 178.A
Schoenfeld, Lowell(1920-) 328
Schoenfinkel, M. 97.*
Schoenflies notation (for crystal classes) 92.E App. Table
Schoenflies problem 65.G
Schoenflies theorem 65.G
Schoenflies, Arthur Moritz(1853-1928) 47.r 65.G 92.E 92.F 93.D 93.K 122.H 381.r App.B Table
Schoenhage, Arnold 298.r
Scholtz, Arnold 59.F
Schopf, Andreas 200.I
Schottky group 234.B
Schottky theorem 43.J
Schottky uniformization 367.C
Schottky, Friedrich Hermann(1851-1935) 9.J 43.J 234.B 367.C
Schouten, Jan Arnoldus(1883-1971) 109.* 109.r 137 417.r 428.r 434.C
Schrader axioms, Osterwalder — 150.F
Schrader, Robert(1939-) 150.F
Schreier conjecture (on simple groups) 151.I
Schreier extension, Artin — (of a field) 172.F
Schreier, Otto(1901-1929) 7.r 28 151.A 151.I 161.A 172.F 190.G 190.N 200.M 256.r 343.r 350.r
Schroeder equation, Koenigs — 44.B
Schroeder functional equation 388.D
Schroeder, A. 156.B
Schroeder, Friedrich Wilhelm Karl Ernst(1841-1902) 44.B 388.D 411.A
Schroedinger equation 351.D
Schroedinger equation 1-body 351.E
Schroedinger equation random 340.E
Schroedinger equation time-dependent 351.D
Schroedinger equation time-independent 351.D
Schroedinger operator 351.D
Schroedinger picture 351.D
Schroedinger representation 351.C
Schroedinger series, Rayleigh — 331.D
Schroedinger, Erwin(1887-1961) 331.A 331.D 340.E 351.C 351.D 434.C
Schubauer, G.B. 433.A
Schubert cycle 56.E
Schubert variety 56.E
Schubert, Hermann(1848-1911) 56.E 201.r
Schubert, Horst(1919-) 235.A
Schuette, Kurt(1909-) 97.* 156.E 156.r
Schur index (of a central simple algebra) 29.E
Schur index (of an irreducible representation) 362.F
Schur lemma (on linear representations) 362.C
Schur lemma (on simple modules) 277.H 368.G
Schur lemma (on unitary representations) 437.D
Schur subgroup 362.F
Schur theorem (on linear transformations of sequences) 379.L
Schur theorem, Kojima — (on linear transformations of sequences) 379.L
Schur — Zassenhaus theorem (on Hall subgroups) 151.E
Schur, Friedrich Heinrich(1856-1932) 364.D
Schur, Issai(1875-1941) 29.E 43.J 122.C 122.E 122.F 122.H 122.r 151.E 226.r 277.H 295.E 368.G 379.L 437.D 437.EE App.B Table
Schuur, Jerry Dee(1936-) 290.r
Schwank, Friedrich(1900-) 217.r
Schwartz integral, Bartle — Dunford — 443.G
Schwartz space 424.S
Schwartz — Christoffel transformation 77.D App. Table
Schwartz — Christoffel transformation formula 77.D
Schwartz, Arthur J.(1932-) 126.I
Schwartz, Jacob Theodore(1930-) 37.r 68.M 112.I 112.O 136.B 136.r 286.r 308.F 308.r 310.r 315.r 331.r 378.r 390.r 443.A 443.G 443.r
Schwartz, Laurent(1915-) 20.* 20.r 68.r 94.r 112.D 112.r 125.A 125.B 125.L 125.r 160.r 162.* 162.r 168.r 189.r 192.M 240.r 262.r 270.I 306.A 322.r 424.R 424.S 424.X 424.r
Schwartz, Richard 280.r
Schwarz inequality 211.C
Schwarz inequality Cauchy — 211.C App. Table
Schwarz lemma 43.B
Schwarz principle of reflection 198.G
Schwarz, Hermann Amandus(1843-1921) 11.D 43.B 77.D 106.H 109 198.G 211.C 246.B 275.B 275.F 334.C App.A Tables 9.III 13.III
Schwarzenberger, Rolph Ludwig Edward(1936-) 92.r
Schwarzian derivative App. A Table
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -
-