|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Machine-language program 75.C
Machover, Maurice(1931-) 356.G
Mack method, Garside — Jarratt — 301.N
Mack, C 301.N
Mackay, Alan L. 92.F
MacKenzie, Robert E.(1920-) 279.C
Mackey space 424.N
Mackey theorem 424.M
Mackey topology 424.N
Mackey — Arens theorem 424.N
Mackey, George Whitelaw(1916-) 36.G 424.M 424.N 437.EE
MacLane complexes, Eilenberg — 70.F
MacLane space, Eilenberg — 70.F
MacLane spectrum, Eilenberg — 202.I
MacLane, Saunders(1909-) 8.r 52.r 70.F 70.r 91.r 103.r 200.M 200.r 201.G 202.T 277.r 305.A
Maclaurin formula, Euler — 379.J
Maclaurin, Colin(1698-1746) 20 266 379.J
MacMahon, Major Percy Alexander(1854-1929) 328 330.r
MacPherson, Robert Duncan(1944-) 366.E 336.r
MacRobert, Thomas Murray 393.r
Macroeconomic data 128.A
Macroscopic causality (of S-matrix) 386.C
Madansky, Albert 408.r
Maeda, Fumi-Yuki(1935-) 207.D 207.r
Maeda, Fumitomo(1897-1965) 162
Maeda, Yoshiaki(1948-) 364.G
Maehara, Shoji(1927-) 411.J 411.r
Magenes, Enrico(1923-) 112.E 323.r
Magentic viscosity 259
Magidor, Menachem 33.r
Magnetic field 130.A
Magnetic flux density 130.A
Magnetic group 92.D
Magnetic induction 130.A
Magnetic permeability 130.B
Magnetic polarization 130.A
Magnetic quantum number, orbital 351.E
Magnetic Reynolds number 259
magnetic susceptibility 130.B
Magnetic wave 130.B
Magnetic wave transverse 130.B
Magnetofluid dynamics 259
Magnetohydrodynamics 259
Magnetostatics 130.B
Magnitude (of a vector) 442.B
Magnus, Wilhelm(1907-) 161.B 161.r 389.r App.A Table
Mahalanobis generalized distance 280.E
Mahalanobis, Prasanta Chandra(1893-1972) 280.E
Mahler, Kurt(1903-) 182.r 430.B 430.C
Mahlo, p. 33.r
Main classes 241. A
Main effect 102.H
Main theorem (in class field theory) 59.C
Main theorem Zariski’s 16.I
Mainardi equations, Codazzi — 111.H App. Table
Mainardi, Gaspare(1800-1879) 111.H App.A Table
Maitra, Ashok P. 22.E 396.r
Majima, Hideyuki(1952-) 428.H
Major arc 4.B
Major axis (of an ellipse) 78.C
Major function 100.F
Majorant (of a sequence of functions) 435.A
Majorant harmonic (of a subharmonic function) 193.S
Majorant series 316.G 435.A
Majorant, method of 316.G
Majorizing function, right 316.E
Makarov, Vitalii Sergeevich(1936-) 122.G
Malcolm, Donald G. 376.r
Malfatti problem (in geometric construction) 179.A
Malfatti.Gian Francesco(1731-1807) 179.A
Malgrange theorem, Ehrenpreis — 112.B
Malgrange, Bernard(1928-) 58.C 58.E 68.F 112.B 112.C 112.R 125.W 320.H 418.r 428.H
Malhavin, Paul(1925-) 115.D 115.r 192.M 406.E 406.r
Malmquist, Johannes(1882-1952) 254.D 288.B 288.C 288.r 289.B—D 314.A
Malus theorem 180.A
Malus, Etienne Louis(1775-1812) 180.A
Mal’tsev theorem, Wedderburn- (on algebras) 29.F
Mal’tsev — Iwasawa theorem, Cartan- (on maximal compact subgroups) 249.S
Mal’tsev, Anatolii Ivanovich(1909-1967) 29.F 249.S 276.D
Mandelbaum, Richard(1946-) 114.r
Mandelbrojt, Szolem(1899-1983) 58.F 134.C 134.r 339.A 339.r
Mandelbrot, Benoit B.(1924-) 246.K 433.r
Mandelstam representation 132.C
Mandelstam, Stanley(1928-) 132.C
Mane, Ricardo 126.J
Mangasarian, Olvi L.(1934-) 292.D 292.r
Mangoldt function 123.B
Mangoldt, Hans Carl Friedrich von(1854-1925) 123.B 450.B
Manifold(s)  - 105.D - 105.D
Manifold(s)  -, with boundary 105.E -, with boundary 105.E
Manifold(s)  -, without boundary 105.E -, without boundary 105.E
Manifold(s) 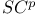 - 178.G - 178.G
Manifold(s)  - 114.I - 114.I
Manifold(s) almost complex 72.B
Manifold(s) almost contact 110.E
Manifold(s) almost parallelizable 114.I
Manifold(s) at a point 178.G
Manifold(s) Banach 105.Z 286.K
Manifold(s) Blaschke manifold 178.G
Manifold(s) center, theorem 286.V
Manifold(s) characteristic (of a partial differential equation) 320.B
Manifold(s) closed 105.B
Manifold(s) coherently oriented pseudo- 65.B
Manifold(s) combinatorial 65.C
Manifold(s) compact  - 105.D - 105.D
Manifold(s) complex analytic 72.A
Manifold(s) conic Lagrange 345.B
Manifold(s) conic Lagrangian 274.C
Manifold(s) contact 110.E
Manifold(s) covering 91.A
Manifold(s) covering differentiable 91.A
Manifold(s) differentiable, of class  105.D 105.D
Manifold(s) differentiable, with boundary of class  105.E 105.E
Manifold(s) fibered 428.F
Manifold(s) Finsler 286.L
Manifold(s) flag 199.B
Manifold(s) Frechet 286.K
Manifold(s) G- 431.C
Manifold(s) group (of a Lie transformation) 110.A
Manifold(s) h-cobordant oriented 114.I
Manifold(s) Hilbert 105.Z 286.K
Manifold(s) Hodge 232.D
Manifold(s) homology 65.B
Manifold(s) Hopf 232.E
Manifold(s) hyperbolic 21.O 235.E
Manifold(s) integral 428.A 428.B 428.D
Manifold(s) irreducible 3- 65.E
Manifold(s) k-dimensional integral 191.I
Manifold(s) Kaehler 232
Manifold(s) nontrivial 3- 65.E
Manifold(s) ordinary integral (of a differential ideal) 428.E
Manifold(s) orientable ( -manifold) 105.F -manifold) 105.F
Manifold(s) orientation 201.N
Manifold(s) oriented 105.F 201.N
Manifold(s) oriented G- 431.E
Manifold(s) paracompact  - 105.D - 105.D
Manifold(s) parallelizable 114.I
Manifold(s) PL- 65.C
Manifold(s) Poincare 105.A
Manifold(s) prime 3- 65.E
Manifold(s) proper flag 199.B
Manifold(s) pseudo- 65.B
Manifold(s) pseudo-Hermitian 344.F
Manifold(s) Q- 382.D
Manifold(s) real analytic 105.D
Manifold(s) regular integral (of a differential ideal) 428.E
Manifold(s) s-parallelizable 114.I
Manifold(s) singular integral (of a differential ideal) 428.E
Manifold(s) smooth 105.D 114.B
Manifold(s) space-time 359.D
| Manifold(s) stable 126.G 126.J
Manifold(s) stably almost complex 114.H
Manifold(s) stably parallelizable 114.I
Manifold(s) Stein 21.L
Manifold(s) symplectic 219.C
Manifold(s) topological 105.B
Manifold(s) triangulated 65.B
Manifold(s) unstable 126.G 126.J
Manifold(s) visibility 178.F
Manifold(s) weakly 1-complete 21.L
Manifold(s) weakly almost complex 114.H
Manifold(s) with a handle attached by f 114.F
Manifold(s) with boundary 105.B
Manifold(s) with Euclidean connection 109
Manifold(s) without boundary 105.B
Manifold(s), characteristic classes of 56.F
Manin connection, Gauss- (of a variety) 16.V
Manin, V.G. 80.r
Manin, Yurii Ivanovich(1937-) 16.J 16.V 80.r 118.E 387.r 450.J 450.M
Mann — Whitney U-test 371.C
Mann, Henry Berthold(1905-) 4.A 371.A 371.C 421.r
Mann, Larry N.(1934-) 364.F
Manna, Zohar(1939-) 75.r
Mannheim curve 111.F
Mannheim, Amedee(1831-1906) 111.F
Manning, Anthony Kevin(1946-) 51.r 126.J 126.K
MANOVA (multivariate analysis of variance) 280.B
Mansfield, Richard B.(1941-) 22.F
Mantissa (of the common logarithm) 131.C
Many body problem 402.F 420.A
Many-valued (analytic function) 198.J
Many-valued function 165.B
Many-valued logic 411.L
MAP 381.C see
Map bundle 147.B
Map covering 91.A
Map cubic 157.B
Map equivariant 431.A
Map first-return 126.C
Map G- 431A
Map Gauss 111.G
Map Kodaira — Spencer 72.G
Map linear fiber 114.D
Map normal 114.J
Map PL 65.A
Map Poincare 126.C
Map time-one 126.C
Map trivalent 157.B
Mapping 381.C
Mapping  - 105.J - 105.J
Mapping 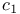 - 237.G - 237.G
Mapping A-balanced 277.J
Mapping affine 7.E
Mapping alternating multilinear 256.H
Mapping analytic 21.J
Mapping antiholomorphic 195.B
Mapping antisymmetric multilinear 256.H
Mapping biadditive 277.J
Mapping biholomorphic 21.J
Mapping bijective 381.C
Mapping bilinear 256.H 277.J
Mapping birational 16.I
Mapping biregular (between prealgebraic varieties) 16.C
Mapping Borel isomorphic 270.C
Mapping bundle 147.B
Mapping CE 382.D
Mapping cellular (between cell complexes) 70.D
Mapping chain 200.C 201.B
Mapping chain (between chain complexes) 201.B
Mapping characteristic (in the classification theorem of fiber bundles) 147.G
Mapping class 202.B
Mapping classifying 147.G
Mapping closed 425.G
Mapping cochain 200.F 201.H
Mapping complete 241.C
Mapping cone 202.E
Mapping cone reduced 202.F
Mapping conformal 198 A
Mapping conjugation (of a Hopf algebra) 203.E
Mapping constant 381.C
Mapping continuous 425.G
Mapping covering 91.A
Mapping cylinder 202.E
Mapping degenerate 208.B
Mapping degree 99.A
Mapping diagonal (of a graded coalgebra) 203.B 203.F
Mapping differentiable, of class  105.J 105.J
Mapping dual (of a linear mapping) 256.G
Mapping duality 251.J
Mapping equivariant 431.A
Mapping essential 202.B
Mapping exponential 178.A 249.Q 364.C
Mapping extremal horizontal slit 367.G
Mapping extremal quasiconformal 352.C
Mapping extremal vertical slit 367.G
Mapping first-return 126.C
Mapping Fredholm 286.E
Mapping G- 362.B 431.A
Mapping Gauss (in geometric optics) 180.B
Mapping generalized conformal 246.I
Mapping harmonic 195.B
Mapping hereditarily quotient 425.G
Mapping holomorphic 21.J 72.A
Mapping homological 200.C
Mapping homotopy-associative 203.D
Mapping Hopf 147.E
Mapping identity 381.C
Mapping inclusion 381.C
Mapping inverse 381.C
Mapping inverse, theorem 208.B
Mapping isometric 111.H 273.B
Mapping Kodaira — Spencer 72.G
Mapping linear (between linear spaces) 256.B
Mapping linear (between polyhedrons) 70.C
Mapping linear fiber 114.D
Mapping meromorphic 23.D
Mapping monotone 311.E
Mapping multilinear 256.H
Mapping nondegenerate holomorphic (between analytic spaces) 23.C
Mapping nonexpansive 286.B
Mapping nonsingular, of class 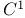 208.B 208.B
Mapping normal 114.J
Mapping normal coordinate 364.C
Mapping of bounded variation 246.H
Mapping of class  208.B 208.B
Mapping of group algebra 192.Q
Mapping one-to-one 381.C
Mapping onto 381.C
Mapping open 425.G
Mapping order-preserving 311.E
Mapping orientation-preserving 99.A
Mapping orientation-reversing 99.A
Mapping partial (of a mapping) 381.C
Mapping perfect 425.W
Mapping perspective (in projective geometry) 343.B
Mapping piecewise affine 192.Q
Mapping piecewise linear (between polyhedra) 70.C
Mapping PL 65.A
Mapping Poincare 126.C 126.G
Mapping product 425.K
Mapping projective (in projective geometry) 343.B
Mapping proper 425.W
Mapping purely inseparable rational 16.I
Mapping quasiconformal 352.B
Mapping quasiperfect 425.CC
Mapping quotient 425.G
Mapping rational 16.I
Mapping regular (between prealgebraic varieties) 16.C
Mapping regular, of class 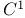 208.B 208.B
Mapping s.s. (semisimplicial)(between s.s. complexes) 70.E
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -
- 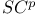 -
-  -
- 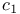 -
-