|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Law(s) arcsine (for random walk) 260.E
Law(s) associative (for addition) 294.B
Law(s) associative (for multiplication) 294.B
Law(s) associative (in a lattice) 243.A
Law(s) associative (in a ring) 368.A
Law(s) associative (in algebra of sets) 381.B
Law(s) associative (of correspondences) 358.B
Law(s) associative (of group composition) 190.A
Law(s) Blumenthai zero-one 261.B
Law(s) Brandt’s 241.C
Law(s) cancellation (for addition) 294.B
Law(s) cancellation (for multiplication) 294.B
Law(s) cancellation (in a commutative semigroup) 190.P
Law(s) commutative (for addition) 294.B 368.A
Law(s) commutative (for multiplication) 294.B 368.A
Law(s) commutative (in a lattice) 243.A
Law(s) commutative (in algebra of sets) 381.B
Law(s) commutative (of group composition) 190.A
Law(s) complementary, of quadratic reciprocity of Jacobi symbol 297.I
Law(s) complementary, of reciprocity 14.O
Law(s) complete distributive (in a lattice-ordered group) 243.G
Law(s) de Morgan’s (in a Boolean algebra) 42.A
Law(s) de Morgan’s (in algebra of sets) 381.B
Law(s) differential 107.A
Law(s) distributive (in a lattice) 243.E
Law(s) distributive (in a ring) 368.A
Law(s) distributive (in algebra of sets) 381.B
Law(s) distributive (of natural numbers) 294.B
Law(s) even-oddness conservation 150.D
Law(s) explicit reciprocity (of norm-residue symbol) 14.R 257.H
Law(s) first complementary, of quadratic reciprocity of Legendre symbol 297.I
Law(s) Gel’fand — Pyatetskii — Shapiro reciprocity (on unitary representations) 437.DD
Law(s) general associative (for group composition) 190.C
Law(s) Hewitt — Savage zero-one 342.G
Law(s) Hooke’s 271.G
Law(s) idempotent (in a lattice) 243.A
Law(s) initial (for stochastic differential equation) 406.D
Law(s) Joule’s 130.B
Law(s) Kepler’s first 271.B
Law(s) Kepler’s second 271.B
Law(s) Kepler’s third 271.B
Law(s) Kirchhoff 282.B
Law(s) Kolmogorov zero-one 342.G
Law(s) law(s) of small numbers 250.B
Law(s) Maxwell — Boltzmann distribution 402.B
Law(s) modular (in a lattice) 243.F
Law(s) Newton (on frictional stresses) 205.C
Law(s) Newton’s first 271.A
Law(s) Newton’s second 271.A
Law(s) Newton’s third 271.A
Law(s) of action and reaction 271.A
Law(s) of complementation (in a Boolean algebra) 42.A
Law(s) of composition 409.A
Law(s) of composition, external 409.A
Law(s) of composition, internal 409.A
Law(s) of cosines (on spherical triangles) 432.B App. Table
Law(s) of cosines, first 432.A App. Table
Law(s) of cosines, second 432.A App. Table
Law(s) of cotangents App. A Table
Law(s) of excluded middle 156.C 411.L
Law(s) of inertia 271.A
Law(s) of inertia, Sylvester (for a quadratic form) 348.C
Law(s) of iterated logarithm 45.F
Law(s) of iterated logarithm, Khinchin 250.C
Law(s) of large numbers 250.B 395.B
Law(s) of large numbers, strong 250.C
Law(s) of motion 271.A
Law(s) of motion, Newton’s three 271.A
Law(s) of quadratic reciprocity of Jacobi symbol 297.I
Law(s) of quadratic reciprocity of Legendre symbol 297.I
Law(s) of reaction 271.A
Law(s) of reciprocity 14.O 297.I
Law(s) of reciprocity, Artin general 59.C
Law(s) of reciprocity, general 14.O
Law(s) of similarity, Prandtl — Glauert 205.D
Law(s) of similarity, Reynolds 205.C
Law(s) of similitude 116
Law(s) of sines 432.A App. Table
Law(s) of sines (for spherical triangles) 432.B App. Table
Law(s) of sines and cosines App. A Table
Law(s) of symmetry (for the Hilbert norm-residue symbol) 14.R
Law(s) of tangents App. A Table
Law(s) of universal gravitation 271.B
Law(s) Ohm 130.B 259
Law(s) reciprocity, of Shafarevich 257.H
Law(s) reflexive (for an equivalence relation) 135.A
Law(s) reflexive (for ordering) 311.A
Law(s) second complementary, of quadratic reciprocity of Legendre symbol 297.I
Law(s) symmetric (for an equivalence relation) 135.A
Law(s) transitive (for an equivalence relation) 135.A
Law(s) transitive (for ordering) 311.A
Law(s) zero-one 342.G
Lawler, Eugene L.(1933-) 66.r 281.r 376.r
Lawley, Derrick Norman 280.B 280.G 280.r 346.F 346.r
Lawson, Charles L. 302.r
Lawson, Herbert Blaine, Jr.(1942-) 80.r 154.r 178.r 275.F 275.r 364.H 365.K
Lax equivalence theorem 304.F
Lax representation 287.B 387.C
Lax — Wendroff scheme 304.F
Lax, Peter David(1926-) 112.J 112.P 112.S 204.r 274.r 304.F 321.G 325.H 345.A 345.r 375.H 387.C 387.r
Layer boundary 205.C
Layer potential of double 338.A
Layer potential of single 338.A
Layout, two-way 155.H
Lazard, Daniel(1941-) 200.K
Lazard, Michel Paul(1924-) 122.F
Lazarov, Connor(1938-) 154.H
LBA problem 31.F
LCL (lower control limit) 404.B
Le Cam theorem 399.K
Le Dung Trang(1947-) 418.I
Le Veque, William Judson(1923-) 118.r 295.r 296.r 297.r 430.r
Leadbetter, Malcolm Ross(1931 ) 395.r
Leaf (leaves) (of a foliation) 154.B
Leaf compact 154.D
Leaf topology 154.D
Leaf, growth of 154.H
Learning model 346.G
Least action, principle of 441.B
Least common multiple 67.H 297.A
Least element (in an ordered set) 311.B
Least favorable a priori distribution 398.H
Least favorable distribution 400.B
Least square approximation 336.D
Least squares estimator 403.E
Least squares estimator generalized 403.E
Least squares method indirect (in econometrics) 128.C
Least squares method three-stage 128.C
Least squares method two-stage 128.C
Least squares problem, linear 302.E
Least squares, method of (for estimation) 403.E
Least squares, method of (for higher-dimensional data) 397.J
Least squares, method of (for numerical solution) 303.I
Least upper bound (ordered sets) 310.C 311.B
Lebesgue area (of a surface) 246.C
Lebesgue convergence theorem 221.C
Lebesgue decomposition theorem 270.L 380.C
Lebesgue density theorem 100.B
Lebesgue dimension 117.B
Lebesgue extension 270.D
Lebesgue integrable 221.B
Lebesgue integral 221.B
Lebesgue measurability and the Baire property 33.F
Lebesgue measurable (set) 270.G
Lebesgue measurable function 270.J
Lebesgue measure 270.G
Lebesgue measure generalized 270.E
Lebesgue measure space (with a finite  -finite measure) 136.A -finite measure) 136.A
Lebesgue method of summation 379.S
Lebesgue number 273.F
| Lebesgue outer measure 270.G
Lebesgue spectrum, countable 136.E
Lebesgue test (on the convergence of Fourier series) 159.B
Lebesgue theorem (on the dimension of 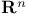 ) 117.D ) 117.D
Lebesgue theorem Borel — 273.H
Lebesgue theorem Cantor — 159.J
Lebesgue theorem Riemann — 159.A 160.A
Lebesgue — Radon integral 94.C
Lebesgue — Stieltjes integral 94.C 166.C
Lebesgue — Stieltjes measure 166.C 270.L
Lebesgue, H.L. 244
Lebesgue, Henri Leon(1875-1941) 20.r 22.A 84.D 93.F 94.C 94.r 117.B 117.D 117.r 120.A 120.B 120.D 136.A 136.E 156.C 159.A—C 159.J 160.A 166.C 168.B 179.r 221.A—C 244 246.C 270.D 270.E 270.G 270.J 270.L 270.r 273.F 379.S 380.C 380.D 380.r 388.B
Lebowitz, A. 134.r
Lebowitz, Joel Louis(1930-) 136.G
LeCam, Lucien(Marie)(1924-) 341.r 398.r 399.K 399.M 399.N 399.r
Ledger, Arthur Johnson(1926-) 364.r
Lee Tsung Dao(1926-) 359.C
Lee, Benjamin W.(1935-1977) 132.r
Lee, E.Bruce(1932-) 86.r
Lee, Y.W. 95.r
Leech, John 151.I
Leela, S. 163.r
Lefebvre, Henri(1905-) 101.r
Lefschetz duality theorem, Poincare — 201.O
Lefschetz fixed-point formula 450.Q
Lefschetz fixed-point theorem 153.B
Lefschetz formula, Picard — 418.F
Lefschetz number (of a continuous mapping) 153.B
Lefschetz number (of a variety) 16.P
Lefschetz pencil 16.U
Lefschetz theorem strong 16.U
Lefschetz theorem weak 16.U
Lefschetz transformation, Picard — 16.U
Lefschetz, Solomon(1884-1972) 3.A 12.B 15.B 16.P 16.U 16.V 79.r 93.r 126.A 126.r 146.r 153.B 153.C 153.r 170.r 201.A 201.E 201.O 201.r 210.r 290.r 291.r 394.r 410.r 418.F 418.I 422.r 426.* 426.r 450.Q
Left  -ideal 27 A -ideal 27 A
Left A-module 277.D
Left adjoint functor 52.K
Left adjoint linear mapping 256.Q
Left annihilator 29.H
Left Artinian ring 368.F
Left balanced functor 200.I
Left continuous 84.B
Left coset 190.C
Left coset space 423.E
Left decomposition, Peirce (in a unitary ring) 368.F
Left derivative 106.A
Left derived functor 200.I 200.Q
Left differentiable 106.A
Left distributive law 312.C
Left endpoint (of an interval) 355.C
Left exact functor 200.I
Left G-set 362.B
Left global dimension (of a ring) 200.K
Left hereditary ring 200.K
Left ideal 368.F
Left ideal integral 27.A
Left invariant Haar measure 225.C
Left invariant metric (of a topological group) 423.I
Left invariant tensor field (on a Lie group) 249.A
Left inverse element (in a ring) 368.B
Left linear space 256.A
Left Noetherian ring 368.F
Left operation 409.A
Left order (of a 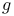 -lattice) 27.A -lattice) 27.A
Left parametrix 345.A
Left projective resolution (of an A-module) 200.C
Left projective space 343.F
Left quotient space (of a topological group) 423.E
Left regular representation (of a group) 362.B
Left regular representation (of an algebra) 362.C
Left resolution (of an A-module) 200.C
Left satellite 200.I
Left semi-integral 68.N
Left semihereditary ring 200.K
Left shunt 115.B
Left singular point (of a diffusion process) 115.B
Left translation 249.A 362.B
Left uniformity (of a topological group) 423.G
Left, limit on the 87.F
Legendre associated differential equation 393.A
Legendre coefficient 393.B
Legendre differential equation 393.B App. Table
Legendre function 393.B App. Table
Legendre function associated App. A Table
Legendre function associated (of the first kind) 393.C App. Table
Legendre function associated (of the second kind) 393.C App. Table
Legendre function of the first kind 393.B App. Table
Legendre function of the second kind 393.B App. Table
Legendre polynomial 393.B App. Table
Legendre relation 134.F App. Table
Legendre symbol 297.H
Legendre symbol first complementary law of reciprocity of 297.I
Legendre symbol second complementary law of reciprocity of 297.I
Legendre symbol, law of quadratic reciprocity of 297.I
Legendre transform 419.C
Legendre transformation (contact transform) 82.A App. Table
Legendre — Jacobi standard form 134.A App. Table
Legendre, Adrien Marie(1752-1833) 4.D 46.C 82.A 83.B 107.A 109 123.A 134.A 134.F 145 174.A 266 296.A 296.B 297.H 297.I 342.A 393.A—C 419.C App.A Tables 15.IV 16.I IV 18.II III
Lehman, R.Sherman(1930-) 385.r 450.I
Lehmann representation, Kaellen — 150.D
Lehmann theorem 371.C
Lehmann theorem Hodges — 399.E 399.H
Lehmann weight, Kaellen — 150.D
Lehmann — Scheffe theorem 399.C
Lehmann — Stein theorem 400.B
Lehmann, Erich Leo(1917 ) 371.A 371.C 371.H 371.r 396.r 399.C 399.E 399.H 399.P 399.r 400.B 400.r
Lehmann, Harry Paul(1924-) 150.D
Lehmer method 301.K
Lehmer, Derrick Henry(1905-) 145 301.K 354.B
Lehmer, Derrick Norman(1867-1938) 123.r NTR
Lehmer, Emma(1906-) 145
Lehner, Joseph(1912-) 32.r
Lehrer, G.I. App.B Table
Lehto, Olli(1925-) 62.C 352.C
Leibenzon(Leibenson), Zinovii Lazarevich(1931-) 192.Q
Leibler (K-L) information number, Kullback — 398.G
Leibler, Richard Arthur(1914-) 398.G
Leibniz formula (in differentiation) 106.D App. Table
Leibniz test (for convergence) 379.C
Leibniz, G.W. 245
Leibniz, Gottfried Wilhelm, Freiherr von(1646-1716) 20 38 75.A 106.D 107.A 156.B 165.A 245 265 283 293.A 332 379.C App.A Tables 10.III
Leith, Cecil Eldon, Jr.(1923-) 433.C
Leja, Franciszek(Francois)(1885-1979) 48.D
Lelong, Pierre(1912-) 21.r
Lelong-Ferrand, Jacqueline(1918—) 364.r
Lemaire, Luc R.(1950-) 195.E 195.r
Lemniscate 93.H
Lemniscate Bernoulli 93.H
Length 246
Length  -(of a group) 151.F -(of a group) 151.F
Length (of a broken line) 139.F
Length (of a curve) 93.F 246.A
Length (of a descending chain in a lattice) 243.F
Length (of a module) 277.I
Length (of a multi-index) 112.A
Length (of a normal chain in a group) 190.G
Length (of a path) 186.F
Length (of a segment) 139.C
Length (of a Witt vector) 449.B
Length affine 110.C
Length affine arc 110.C
Length extremal (of a family of curves) 143.A
Length extremal, defined by Hersch — Pfluger 143.A
Length extremal, with weight 143.B
Length focal 180.B
Length of finite (module) 277.I
Length queue 260.H
Length wave 446
Lens space 91.C
Lens space infinite 91.C
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -finite measure)
-finite measure)  )
)  -ideal
-ideal  -lattice)
-lattice)  -(of a group)
-(of a group)