|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Wallace, Andrew Hugh(1926-) 114.F 114.L
Wallach, Nolan R. 178.r 199.r 249.r 275.A 275.F 364.r 365.G 437.W
Wallis formula App. A Table
Wallis test, Kruskal — 371.D
Wallis, Jennifer Seberry 241.r
Wallis, John(1616-1703) 20 265 332 App.A Table
Wallis, Walter Denis 241.r
Wallis, Wilson Allen(1912-) 371.D
Wallman, Henry(1915-) 117.r
Walsh system of orthogonal functions 317.C
Walsh, John Joseph(1948-) 117.I
Walsh, Joseph Leonard(1895-1973) 223.r 317.C 336.F 336.I
Walter, J.S. 142.C
Walter, John H.(1927-) 151.J
Walter, Wolfgang(1927-) 211.r
Walters, Peter(1943-) 136.H
Walther, Hansjoachim 186.r
Wandering 126.E
Wandering point 126.E
Wandering set 136.C
Wandering set weakly 136.C
Wandering weakly, under a group 136.E
Wang exact sequence (of a fiber space) 148.E
Wang Hsien-Chung(1918-1978) 81 110.E 148.E 152.r 199.r 413.r
Wang Xiaotong(c.early 7th century) 57.A
Wang, Ju-Kwei(1934-) 164.G
Wantzel, Pierre-Laurent(1814-1848) 179.A
Ward, Harold Nathaniel(1936-) App.B Table
Ward, R. 16.r
Waring problem 4.E
Waring, Edward(1736-1798) 4.E
Warner.Frank Wilson, III(1938-) 364.H
Warner.Garth William Jr.(1940-) 249.r 437.r
Warning second theorem 118.B
Warning theorem 118.B
Warning, E. 118.B
Warschawski, Stefan Emanuel(1904-) 77.C
Wasan 230
Washington, A. 432.r
Washington, Lawrence Clinton(1951-) 14.L 450.J
Washio, Yasutoshi(1929-) 399.r
Washizu, Kyuichiro(1921-81) 271.r
Wasow, Wolfgang Richard(1909-) 25.B 25.r 30.r 107.r 254.r 289.E 304.r
Wassermann, Gordon 51.r
Watabe,Tsuyoshi(1934-) 431.D
Watanabe, Kinji(1946-) 323.J
Watanabe, Shinzo(1935-) 44.E 44.r 45.r 115.C 115.r 261.r 262.r 406.B 406.D 406.F
Watanabe, Takeshi(1931-) 260.J
Watari, Chinami(1932-) 336.D
Water wave(s) 205.F
Water wave(s) deep 205.F
Water wave(s) long 205.F
Water wave(s) shallow 205.F
Waternaux, Christine M. 280.r
Watson formula 39.E App. Table
Watson process Galton — 44.B
Watson process multi (k)-type Galton — 44.C
Watson transform 160.C 220.B
Watson — Nicholson formula App. A Table
Watson, George Leo(1909-) 4.E 348.r
Watson, George Neville(1886-) 39.E 39.r 160.C 174.r 220.B 268.r 389.r App.A Tables IV NTR
Watson, H.W. 44.B 44.C 44.r
Watt, J.M. 303.r
Wave equation 325.A 446 App. Table
Wave expansion, partial 375.E 386.B
Wave front set 274.B 345.A
Wave front set analytic 274.D
Wave function 351.D
Wave function spheroidal 133.E
Wave guide 130.B
Wave number (of a sine wave) 446
Wave operator 375.B 375.H
Wave operator generalized 375.B
Wave operator incoming 375.B
Wave operator modified 375.B
Wave operator outgoing 375.B
Wave propagation 446
Wave scattering amplitude, partial 375.E
Wave steepness 205.F
Wave(s) 446
Wave(s) Alfven 259
Wave(s) capillary 205.F
Wave(s) dispersive 446
Wave(s) electromagnetic 446
Wave(s) electromagnetic, theory of 130.B
Wave(s) fast 259
Wave(s) gravity 205. F
Wave(s) gravity, long 205.F
Wave(s) longitudinal 446
Wave(s) Mach 205.B
Wave(s) partial 386.B
Wave(s) partial, expansion 375.E 386.B
Wave(s) plane 446
Wave(s) polarized 446
Wave(s) shock 205.B 446
Wave(s) sine 446
Wave(s) sinusoidal 446
Wave(s) slow 259
Wave(s) spherical 446
Wave(s) stationary 446
Wave(s) Stokes 205.F
Wave(s) surface 446
Wave(s) transverse 446
Wave(s) water 205.F
Wave(s) water, deep 205.F
Wave(s) water, long 205.F
Wave(s) water, shallow 205.F
Wavelength (of a sine wave) 446
Wayland, Harold(1909-) 298.r
WC group 118.D
Weak  topology 279.C topology 279.C
Weak (boundary component) 77.E
Weak Bernoulli process 136.E
Weak Bernoulli process very 136.E
Weak convergence (of a sequence of submodules) 200.J
Weak convergence (of operators) 251.C
Weak convergence (of probability measures) 341.F
Weak derivative 125.E
Weak dimension (of a module) 200.K
Weak extension (of a differential operator) 112.E 112.F
Weak form of the boundary value problem (of partial differential equations) 304.B
Weak global dimension (of a ring) 200.K
Weak homotopy equivalence 202.F
Weak lacuna 325.J
Weak law of large numbers 395.B
Weak Lefschetz theorem 16.U
Weak minimum 46.C
Weak Mordell — Weil theorem 118.E
Weak operator topology 251.C
Weak potential kernel 260.D
Weak solution 204.C 323.G 378.I
Weak solution, Hopf’s 204.C
Weak star topology 37.E 424.H
Weak topology (in a cell complex) 70.D
Weak topology (on a class of measures) 338.E
Weak topology (on a direct product space) 425.K
Weak topology (on a direct sum) 425.M
Weak topology (on a locally convex space) 424.H
Weak topology (on a normed linear space) 37.E
Weak topology (relative to the pairing <E,F>) 424.H
Weak topology hereditarily 425.M
Weak type (p,q), quasi-linear operator of 224.E
Weaker (equivalence relation) 135.C
Weaker (method of summation) 379.L
Weaker (topology) 425.H
Weaker (uniformity) 436.E
Weakly 1-complete manifold 114.H
Weakly almost complex manifold 114.H
Weakly compact (linear operator) 68.M
Weakly compact cardinal number 33.E
| Weakly continuous (function with values in a Banach space) 37.K
Weakly continuous representation (of a topological group) 69.B
Weakly dominated (statistical structure) 396.F
Weakly equivalent (transformations) 136.F
Weakly G-stationary (system of random variables) 395.I
Weakly hyperbolic linear (differential operator) 325.H
Weakly inaccessible (cardinal number) 33.E
Weakly inaccessible (ordinal number) 312.E
Weakly integrable 443.F
Weakly isomorphic (automorphisms) 136.E
Weakly measurable 443.B 443.I
Weakly mixing (automorphism) 136.E
Weakly modular 351.L
Weakly nonlinear differential equations 290.D
Weakly stationary process 395.A
Weakly stationary process of degree k 395.I
Weakly stationary random distribution 395.C
Weakly symmetric Riemannian space 412.J
Weakly wandering set 136.C
Weakly wandering under a group 136.F
Weakly, converge (in a normal linear space) 37.E
Weakly, converge (in a topological linear space) 424.H
Weaver, W. 403.r
Web group 234.B
Weber differential equation 167.C App. Table
Weber formula App. A Table
Weber function 167.C App. Table
Weber — Hermite differential equation 167.C
Weber — Sonine formula App. A Table
Weber, Claude Alain(1937-) 65.r
Weber, H.F. 39.G App.A Table
Weber, Heinrich(1842-1913) 8.r 11.B 11.r 12.B 73.A 98 167.C 236.r 363.* 363.r App.A Tables IV 20
Weber, Wilhelm Eduard(1804-1891) 363
Webster, Arthur Gordon(1863-1923) 322.r
Webster, Sidney M.(1945-) 344.F
Wedderburn theorem (on commutativity of finite fields) 149.M
Wedderburn theorem (on simple algebras on a field) 29.E
Wedderburn theorem (on simple rings) 368.G
Wedderburn — Mal’tsev theorem (on algebras) 29.F
Wedderburn, Joseph Henry Maclagan(1882-1948) 29.E 29.F 149.M 190.L 368.G
wedge 125.V
Wedge infinitesimal 125.V
Wedge product (of derived functors) 200.K
Wedge theorem, edge of the 125.W
Wehrl, Alfred(1941-) 212.r
Weierstrass 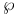 -function 134.F App. Table -function 134.F App. Table
Weierstrass approximation theorem 336.A
Weierstrass canonical form (of elliptic curves) 9.D
Weierstrass canonical form (of the gamma function) 174.A
Weierstrass canonical product 429.B
Weierstrass criterion for uniform convergence 435.A
Weierstrass elliptic functions 134.F App. Table
Weierstrass point 11.D
Weierstrass preparation theorem 21.E 370.B
Weierstrass sigma function 134.F
Weierstrass theorem (on compactness of subsets of 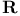 ) 355.D ) 355.D
Weierstrass theorem (on continuous functions on a compact set) 84.C
Weierstrass theorem (on essential singularities) 198.D
Weierstrass theorem (on expansion of meromorphic functions) 272.A
Weierstrass theorem (on transcendental entire functions) 124.B
Weierstrass theorem Lindemann — 430.D
Weierstrass theorem of double series 379.H
Weierstrass theorem, Bolzano — 140 273.F
Weierstrass theorem, Casorati — (on essential singularities) 198.D
Weierstrass zeta function 134.F
Weierstrass — Enneper formula 275.A
Weierstrass — Stone theorem 168.B
Weierstrass, K. 447
Weierstrass, K. analytic function in the sense of 198.I
Weierstrass, Karl Theodor Wilhelm(1815-1897) 9.D 11.B 11.D 20 21.A 21.E 46.C 58.C 84.C 106.B 109 120.A 134.F 140 168.B 174.A 198.D 198.I 198.N 198.Q 229.r 236 267 272.A 273.F 274.F 275.A 275.B 294.A 334.B 334.C 336.A 336.F 339.A 339.D 355.D 355.r 370.B 379.H 429.B 430.D 435.A 447 App.A Table
Weierstrass-type preparation theorem (for microdifferential operators) 274.F
Weight function (for the mean of a function) 211.C
Weight function (in numerical integration) 299.A
Weight function (in orthogonality) 317.A
Weight group (of a pair (T,K)) 92.C
Weight k, automorphic form of 32.B
Weight k, Fuchsian form of 32.B
weight k, Hilbert modular form of 32.B
Weight k, Siegel modular form of 32.F
Weight lattice (of a pair (T, K)) 92.C
Weight m, automorphic form of 32.A
Weight w, invariant of 226.D
Weight(s) (in a barycenter) 7.C
Weight(s) (of a covariant) 226.D
Weight(s) (of a multiple covariant) 226.E
Weight(s) (of a representation of a complex semisimple Lie algebra) 248.W
Weight(s) (of a weighted homogeneous analytic function) 418.D
Weight(s) (of an automorphic form) 32.C
Weight(s) (on a von Neumann algebra) 308.D
Weight(s) equal, principle of 402.E
Weight(s) extremal length with 143.B
Weight(s) highest (of a representation of a complex semisimple Lie algebra) 248.W
Weight(s) Kaellen — Lehmann 150.D
Weighted homogeneous (analytic function) 418.D
Weighted moving average 397.N
Weighting matrix 86.B
Weil cohomology 450.Q
Weil conjecture 450.Q
Weil conjecture Taniyama — 450.S
Weil domain 21.G
Weil group 6.E 450.H
Weil L-function 450.H
Weil measure 225.G
Weil number 3.C
Weil theorem, Borel — 437.Q
Weil theorem, Mordell — 118.E
Weil theorem, weak Mordell — 118.E
Weil — Chatelet group 118.D
Weil, Andre(1906-) 3.C 3.E 3.M 3.r 4.D 6.E 6.r 9.E 9.H 9.r 12.B 12.r 13.M 13.r 14.r 16.A 16.C 20 21.G 27.r 28 32.C 32.D 59.H 59.r 60.O 73.B 109.* 109.r 118.B 118.D 118.E 122.F 122.G 122.r 182.E 192.r 196 225.G 225.r 232.B 422.r 436.A 436.r 437.P 450.A 450.H 450.M 450.O—S 450.r
Weinberg — Salam model, Glashow — 132.D
Weinberg, B.L. 96.r
Weinberg, Louis(1919-) 282.r
Weinberg, N. 425.U
Weinberg, Steven(1933-) 132.C 132.D 132.r
Weinberger, Hans Felix(1928-) 323.r 327.r
Weingarten formula (for an isometric immersion) 365.C
Weingarten formula (in the theory of surface) 111.H App. Table
Weingarten surface 111.I
Weingarten, Leonhard Gottfried Johannes Julius(1836-1910) 111.H 111.I 365.C App.A Table
Weinstein, Alan David(1943-) 126.N 178.r
Weinstock, Robert 441.r
Weir, M.D. 425.r
Weirich formula App. A Table
Weisberger sum rule, Adler — 132.C
Weisberger, William I.(1937-) 132.C
Weiss, Benjamin(1941-) 136.E—G
Weiss, Edwin(1927-) 14.r 200.r
Weiss, Guido Leopold(1928-) 168.B 224.r
Weiss, Lionel(1923-) 398.r
Weiss, Max L.(1933-) 43.r
Weitsman, Allen W. 272.K 272.r
Weitzenboeck, Roland W.(1885-) 226.C
Welch test 400.G
Welch, Bernard Lewis 400.G
Weldon, Edward J. Jr. 63.r
Well-behaved 36.K
Well-chained (metric space) 79.D
Well-measurable 407.B
Well-measurable  -algebra 407.B -algebra 407.B
Well-ordered set 311.C
Well-ordering 311.C
Well-ordering theorem 34.B
Well-posed (initial value problem) 321.E
Well-posed (martingale problem) 115.C
Well-posed (problems for partial differential equations) 322.A
Wells, Raymond O’Neil.Jr.(1940-) 164.K 232.r 344.D 344.E
Welsh, James Anthony Dominic 66.r
Wendroff scheme, Lax — 304.F
Wendroff, Burton 304.F
Wentzel, Gregor(1898-) 25.B
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 topology
topology 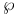 -function
-function 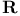 )
)  -algebra
-algebra