|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Valuation(s) discrete 439.E
Valuation(s) equivalent 439.B
Valuation(s) exponential 439.B
Valuation(s) generalized 439.B
Valuation(s) multiplicative 439.C
Valuation(s) non-Archimedean 14.F 439.C
Valuation(s) normal 439.E 439.H
Valuation(s) normalized 439.E
Valuation(s) over a subfield 439.B 439.C
Valuation(s) pseudo- 439.K
Valuation(s) special 439.B
Valuation(s) trivial 439.C.F
Valuation(s), completion of 439.D
Valuation(s), prolongation of 439.B
Value distribution 124.A
Value function 108.B 405.A
Value group (of a multiplicative valuation) 439.C
Value group (of an additive valuation) 439.B
Value(s) (of a variable) 165.C
Value(s) (of an infinite continued fraction) 83.A
Value(s) (of an infinite product) 379.G
Value(s) absolute (of a complex number) 74.B
Value(s) absolute (of a real number) 355.A
Value(s) absolute (of a vector) 442.B
Value(s) absolute (of an element of a vector lattice) 310.B
Value(s) absolute (of an element of an ordered field) 149.N
Value(s) asymptotic (of a meromorphic function) 62.A 272.H
Value(s) boundary (hyperfunction) 125.V
Value(s) boundary (of a conformal mapping) 77.B
Value(s) boundary (relative to a differential operator) 112.E
Value(s) characteristic (of a linear operator) 390.A
Value(s) cluster 62.A
Value(s) cluster, theorem 43.G
Value(s) critical (in bifurcation theory) 286.R
Value(s) critical (of a  -function on a manifold) 279.B -function on a manifold) 279.B
Value(s) critical (of a  -mapping -mapping  ) 105.J ) 105.J
Value(s) critical (of a contact process) 340.C
Value(s) critical (of a mapping u:  ) 208.B ) 208.B
Value(s) critical (of an external magnetic field) 340.B
Value(s) exceptional (of a transcendental entire function) 429.B
Value(s) exceptional, Borel 272.E
Value(s) exceptional, Nevanlinna 272.E
Value(s) exceptional, Picard 272.E
Value(s) expectation (of an observable) 351.B
Value(s) expected (of a random variable) 342.C
Value(s) gap (of a point on a Riemann surface) 11.D
Value(s) initial (for ordinary differential equations) 316.A
Value(s) initial (for partial differential equatons) 321.A
Value(s) initial (for stochastic differential equations) 406.D
Value(s) limit (of a mapping) 87.F
Value(s) mean (of a function on a compact group) 69.A
Value(s) mean (of a weakly stationary process) 395.C
Value(s) most probable 401.E
Value(s) principal (of inverse trigonometric functions) 131.E
Value(s) principal (of log z) 131.G
Value(s) principal, Cauchy (of an improper integral) 216.D
Value(s) principal, Cauchy (of the integral of a function in  216.E 216.E
Value(s) proper (of a boundary value problem) 315.B
Value(s) proper (of a linear mapping) 269.L
Value(s) proper (of a linear operator) 390.A
Value(s) proper (of a matrix) 269.F
Value(s) range of (of a meromorphic function) 62.A
Value(s) regular 105.J
Value(s) sample 396.B
Value(s) sample characteristic 396.C
Value(s) Shapley 173.D
Value(s) singular 302.A
Value(s) singular, decomposition (SVD) 302.E
Value(s) starting 303.E
Value(s) stationary (of a function) 106.L
Value(s) true, of parameter 398.A
Value(s) truth (of a formula) 411.E
van Beijeren, Henk 402.G
van Ceulen, Ludolf(1540-1610) 332
Van Daele, Alfons 308.H
van Dantzig, D. 109 434.C
van den Berg, Franciscus Johannes(1833-1892) 19.B
van der Corput, Johannes Gualtherus(1890-1975) 4.C 182.H 242.A
van der Pol differential equation 290.C
van der Pol, Balthasar(1889-1959) 240.r 290.C
van der Waerden test 371.C
van der Waerden — Bortolotti covariant derivative 417.E
van der Waerden, Bartel Leendert(1903-) 8.* 8.r 12.B 24.r 29.r 60.r 66.r 67.r 90.r 92.F 92.r 122.r 149.r 172.r 187.r 190.r 196 284.r 337.r 351.r 362.r 368.r 369.E 371.C 417.E
van Hove sense, limit in 402.G
van Hove, Leon Charles Prudent(1924-) 351.K 402.G
van Kampen theorem (on fundamental groups) 170
van Kampen, Egbertos R.(1908-1942) 170
Van Moerbeke, Pierre(1944-) 287.C
van Roomen, Adriaan(1561-1615) 444
van Schooten, Frans(1615-1660) 444.r
Vandermonde determinant 103.G
Vandermonde, Alexandre Theophile(1735-1796) 103.G 190.Q
Vandiver conjecture 14.L
Vandiver, Harry Shultz(1882-1973) 14.L 145.* 145.r
Vanishing cocycle 16.U
Vanishing cycle 418.F
Vanishing theorem (on compact complex manifolds) 194.G
Vanishing theorem, Kodaira 232.D
Varadarajan, Veeravalli Seshadri(1937-) 249.r
Varadhan, Sathamangalam Ranga Ayyangar Srinivasa(1940-) 115.C 115.D 115.r 136.r 250.r 261.C 262.E 340.r 406.A 406.D 406.r
Varadier, M. 443.A
Varaiya, Pravin P. 86.D 108.B 292.F
Varchenko, A.N. 418.r
Varga, Otto(1909-1969) 152.C
Varga, Richard Steven(1928-) 302.r
Variability, measure of 397.C
Variable component (of a linear system) 15.C 16.N
Variable method, discrete 303.A
Variable(s) 165.C
Variable(s) (of a polynomial) 369.A
Variable(s) artificial 255.C
Variable(s) auxiliary 373.C
Variable(s) basic 255.A
Variable(s) bound 411.C
Variable(s) canonical (in analytical dynamics) 271.F
Variable(s) change of (in integral calculus) 216.C
Variable(s) complex 165.C
Variable(s) complex, theory of functions of 198.Q
Variable(s) dependent 165.C
Variable(s) differential (of a differential polynomial) 113
Variable(s) endogenous 128.C
Variable(s) exogenous 128.C
Variable(s) explanatory 403.D
Variable(s) hidden, theories 351.L
Variable(s) independent 165.C
Variable(s) individual 411.H
Variable(s) inner 25.B
Variable(s) lagged 128.C
Variable(s) object 411.G
Variable(s) outer 25.B
Variable(s) predetermined 128.C
Variable(s) predicate 411.G 411.H
Variable(s) proposition 411.E
Variable(s) random 342.C
Variable(s) random,  -valued 342.C -valued 342.C
Variable(s) random, 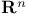 -valued 342.C -valued 342.C
Variable(s) random, independent 342.C
Variable(s) random, joint 342.C
Variable(s) random, n-dimensional 342.C
Variable(s) real 165.C
Variable(s) slack 255.A
Variable(s) state 127. A
Variable(s), sampling inspection by 404.C
Variable(s), separation of 322.C
Variable-step variable-order (VSVO) algorithms 303.E
Variance (of a probability distribution) 341.B
Variance (of a random variable) 342.C
Variance (of univariate quantitative data) 397.C
Variance analysis of 400.H 403.D
Variance between-group 397.L
| Variance generalized 280.E 397.J
Variance matrix 341.B
Variance population 396.C
Variance sample 396.C
Variance sample generalized 280.E
Variance uniformly minimum unbiased estimator 399.C
Variance within-group 397.L
Variance, multivariate analysis of 280.B
Variance-covariance matrix 341.B 397.J
Variate canonical 280.E
Variate fixed 403.D
Variation curve 178.A
Variation vector field 178.A
Variation(s) (of an integral) 100.E
Variation(s) first 46.B
Variation(s) first, formula 178.A
Variation(s) geodesic 178.A
Variation(s) lower (of a set function) 380.B
Variation(s) negative (of a mapping) 246.H
Variation(s) negative (of a real bounded function) 166.B
Variation(s) of parameters, Lagrange method of 252.D
Variation(s) of parameters, method of App. A Table
Variation(s) one-parameter 178.A
Variation(s) positive (of a mapping) 246.H
Variation(s) positive (of a real bounded function) 166.B
Variation(s) proper 279.F
Variation(s) quadratic, process 406.B
Variation(s) second formula 178.A
Variation(s) total (of a finitely additive vector measure) 443.G
Variation(s) total (of a mapping) 246.H
Variation(s) total (of a real bounded function) 166.B
Variation(s) total (of a set function) 380.B
Variation(s) upper 380.B
Variation(s), calculus of 46
Variation(s), calculus of, classical theory of 46.C
Variation(s), calculus of, conditional problems in 46.A
Variation(s), calculus of, fundamental lemma in 46.B
Variation(s), coefficient of 397.C
Variation(s), of constants, Lagrange’s method of 252.D
Variation(s), of constants, method of 55.B 252.I
Variational derivative 46.B
Variational equation 316.F 394.C
Variational formula, constant 163.E
Variational inequality 440
Variational inequality, of evolution 440.C
Variational inequality, stationary 440.B
Variational method 438.B
Variational principles(s) 441
Variational principles(s) (in ergodic theory) 136.G
Variational principles(s) (in statistical mechanics) 340.B 402.G
Variational principles(s) (in the theory of elasticity) 271.G
Variational principles(s) for the topological pressure 136.H
Variational principles(s) with relaxed continuity requirements 271.G
Variational problem, Gauss 338.J
Variety (algebraic variety) 16.A
Variety (of block design) 102.B
Variety Abelian 3
Variety Abelian, isogeneous 3.C
Variety Abelian, polarized 3.G
Variety Abelian, simple 3.B
Variety abstract 16.C
Variety abstract algebraic 16.C
Variety affine 16.A
Variety affine algebraic 16.A
Variety Albanese 16.P
Variety Albanese (of a compact Kaehler manifold) 232.C
Variety algebraic 16
Variety algebraic group 13.B
Variety Brieskorn 418.D
Variety characteristic (of a microdifferential equation) 274.G
Variety Chow 16.W
Variety complex algebraic 16.T
Variety generalized Jacobian 9.F 11.C
Variety group 13.B 16.H
Variety irreducible 16.A
Variety Jacobian 9.E 11.C 16.P
Variety Landau 146.C
Variety Landau — Nakanishi 146.C 386.C
Variety linear (in an  -module) 422.L -module) 422.L
Variety linear, linearly compact 422.L
Variety minimal 275.G
Variety nonsingular 16.F
Variety normal 16.F
Variety normal algebraic 16.F
Variety Picard 16.P
Variety Picard (of a compact Kaehler manifold) 232.C
Variety prealgebraic 16.C
Variety product algebraic 16.A
Variety projective 16.A
Variety projective algebraic 16.A
Variety quasi-affine algebraic 16.C
Variety quasiprojective algebraic 16.C
Variety rational 16.J
Variety reducible 16.A
Variety Schubert 56.E
Variety smooth 16.F
Variety strict Albanese 16.P
Variety toric 16.Z
Variety unirational 16.J
Variety Zariski topology of a 16.A
Variety, almost all points of a 16.A
Variety, function on a 16.A
Variety, rational function on a 16.A
Varifold 275.G
Varopoulos, Nicholas Theodoros 192.U
Varopoulos, T. 17.C 267.r
Varouchas, J. 232.C
Varshamov — Gilbert — Sacks bound 63.B
Varshamov, Rom Rubenovich(1927-) 63.B
Vasilesco, Florin(1897-1958) 120.D
Vaughan, Robert Charles 123.E
Vaught, Robert L. 276.D 276.F
Veblen, Oswald(1880-1960) 90.r 109.* 109.r 137 152.C 201.r 343.r 434.C 434.r
Vector algebra App. A Table
Vector analysis and coordinate systems App. A Table
Vector bundle 147.F
Vector bundle (algebraic) 16.Y
Vector bundle ample 16.Y
Vector bundle complex 147.F
Vector bundle cotangent 147.F
Vector bundle dual 147.F
Vector bundle indecomposable 16.Y
Vector bundle normal 105.L
Vector bundle normal k- 114.J
Vector bundle quaternion 147.F
Vector bundle semistable 16.Y
Vector bundle stable 16.Y 237.B
Vector bundle stably equivalent 237.B
Vector bundle tangent 105.H 147.F
Vector field (in a 3-dimensional Euclidean space) 442.D
Vector field (on a differentiable manifold) 105.M
Vector field Anosov 126. J
Vector field Axiom A 126.J
Vector field basic 80.H
Vector field contravariant 105.O
Vector field covariant 105.O
Vector field differentiation of App. A Table
Vector field formal 105.AA
Vector field fundamental 191.A
Vector field G- 237.H
Vector field Hamiltonian 126.L 219.C
Vector field holomorphic 72.A
Vector field irrotational 442.D
Vector field Killing 364.F
Vector field Lagrangian 126.L
Vector field lamellar 442.D
Vector field Morse — Smale 126.J
Vector field of class  105.M 105.M
Vector field solenoidal 442.D
Vector field variation 178.A
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -function on a manifold)
-function on a manifold)  )
)  )
) 
 -valued
-valued 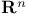 -valued
-valued  -module)
-module) 