|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Decision problem sequential 398.F
Decision problem statistical 398.A
Decision procedure, statistical 398.A
Decision process, Markov 127.E
Decision rule sequential 398.F
Decision rule terminal 398.F
Decision space 398.A
Decision theoretically sufficient  -field 396.J -field 396.J
Decoder 213.D
Decoding 63.A
Decomposable operator (on a Hilbert space) 308.G
Decompose (a polygon) 155.F
Decomposed into the direct sum of irreducible representations 437.G
Decomposition (of a set) 381.D
Decomposition Bruhat (of an algebraic group) 13.K
Decomposition canonical (of a closed operator) 251.E
Decomposition cellular (of a Hausdorff space) 70.D
Decomposition Chevalley (on algebraic groups) 13.I
Decomposition cluster, Hamiltonian 375.F
Decomposition CW 70.D
Decomposition D-optimality 102.E
Decomposition de Rham (of a Riemannian manifold) 364.E
Decomposition direct (of a group) 190.L
Decomposition Doob — Meyer 262.C
Decomposition dual direct product (of a decomposition of a compact or discrete Abelian group) 422.H
Decomposition ergodic (of a Lebesgue measure space) 136.H
Decomposition Fefferman — Stein 168.B
Decomposition field (of a prime ideal) 14.K
Decomposition formula of Radon 125.CC
Decomposition group (of a prime ideal) 14.K
Decomposition Heegurard 65.C
Decomposition Iwasawa (of a connected semisimple Lie group) 249.T
Decomposition Iwasawa (of a real semisimple Lie algebra) 248.V
Decomposition Jordan (in an ordered linear space) 310.B
Decomposition Jordan (of a function of bounded variation) 166.B
Decomposition Jordan (of a linear mapping) 269.L
Decomposition Jordan (of an additive set function) 380.C
Decomposition Khinchin 395.B
Decomposition Lebesgue, theorem 270.L
Decomposition Levi (on algebraic groups) 13.Q
Decomposition Levi (on Lie algebras) 248.F
Decomposition multiplicative Jordan (of a linear transformation) 269.L
Decomposition number (of a finite group) 362.I
Decomposition number generalized (of a finite group) 362.I
Decomposition Peirce (of a Jordan algebra) 231 .B
Decomposition Peirce left (in a unitary ring) 368.F
Decomposition Peirce right (in a unitary ring) 368.F
Decomposition plane wave 125.CC
Decomposition polar 251.E
Decomposition relative Bruhat 13.Q
Decomposition Riesz (in Markov process) 260.D
Decomposition Riesz (in martingale) 262.C
Decomposition Riesz (of a superharmonic or subharmonic function) 193.S
Decomposition semimartigale 406.B
Decomposition simplicial (of a topological space) 79.C
Decomposition singular value (SVD) 302.E
Decomposition spectral 126.J
Decomposition theorem canonical 86.C
Decomposition theorem for dimension 117.C
Decomposition theorem in class field theory 59.C
Decomposition theorem Lebesgue (on a completely additive set function) 380.C
Decomposition theorem unique (for a 3-manifold) 65.E
Decomposition Wiener — Ito 176.I
Decomposition Witt (of a quadratic form) 348.F
Decomposition Wold 395.D
Decomposition Zariski 15.D
Decomposition-equal polygons 155.F
Decreasing  -function, rapidly 168.B -function, rapidly 168.B
Decreasing distribution, rapidly 125.O
Decreasing Fourier hyperfunction, exponentially 125.BB
Decreasing function monotone 166.A
Decreasing function strictly 166.A
Decreasing function strictly monotone 166.A
Decreasing real analytic function, exponentially 125.BB
Decreasing sequence, monotonically (of real numbers) 87.B
Decreasing sequence, monotonically rapidly 168.B
Decreasing, monotone 380.B
Decrement, logarithmic (of a damped oscillation) 318.B
Dedekind axiom of continuity (for real numbers) 355.A
Dedekind discriminant theorem 14.J
Dedekind eta function 328.A
Dedekind principle (in a modular lattice) 243.F
Dedekind sum 328.A
Dedekind sum, reciprocity law for 328.A
Dedekind theory of real numbers 294.E
Dedekind zeta function 14.C 450.D
Dedekind, J.W.R. 98
Dedekind, Julius Wilhelm Richard(1831—1916) 11.B 11.r 12.B 14.C—E 14.J 14.U 47 49.F 49.r 67.K 98 156.A 156.r 172.A 172.r 243.F 267 284.G 294.A 294.E 294.r 328 347.H 355.A 355.r 363.r 379.D 450.A 450.D 450.K
Dedekind, test of du Bois-Reymond and 379.D
Deep water wave 205.F
Defect (of a block of representations) 362.I
Defect (of a conjugate class in a group) 362.I
Defect (of a meromorphic function) 272.E
Defect group (of a conjugate class in a group) 362.I
Defect group of a block of representations 362.I
Deficiency (of a closed operator) 251.D
Deficiency (of a linear system on a surface) 15.C
Deficiency (of an algebroidal function) 17.C
Deficiency index (of a closed symmetric operator) 251.I
Deficiency index (of a differential operator) 112.I
Deficiency maximal (of an algebraic surface) 15.E
Deficient number (in elementary theory of numbers) 297.D
Define recursively 356.C
Defined along 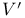 (for a rational mapping) 16.I (for a rational mapping) 16.I
Defined over 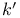 (for an algebraic variety) 16.A (for an algebraic variety) 16.A
Defining functions (of a hyperfunction) 125.V
Defining functions standard 125.Z
Defining ideal (of a formal spectrum) 16.X
Defining module (of a linear system) 16.N
Defining relations (among the generators of a group) 161.A
Definite D-integral 100.D
Definite integral 216.C App. Table
Definite integral (of a hyperfunction) 125.X
Definite negative (function) 394.C
Definite negative (Hermitian form) 348.F
Definite negative (quadratic form) 348.B
Definite positive (function) 36.L 192.B 192.J 394.C 437.B
Definite positive (Hermitian form) 348.F
Definite positive (kernel) 217.H
Definite positive (matrix) 269.I
Definite positive (potential) 338.D
Definite positive (quadratic form) 348.B
Definite positive (sequence) 192.B
Definite quadratic form 348.C
Definite semi- (Hermitian form) 348.F
Definite semi-(kernel) 217.H
Definite totally (quaternion algebra) 27.D
Definition by mathematical induction 294.B
Definition by transfinite induction 311.C
Definition first (of algebraic K-group) 237.J
Definition second (of algebraic K-group) 237.J
Definition truth 185.D
Definition, field of 16.A
Deflation in homological algebra 200.M
Deflation method for an eigenvalue problem 298.C
Deformation (of a graph) 186.E
Deformation (of complex structures) 72.G
Deformation cochain 305.B
Deformation infinitesimal, to the direction 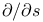 72.G 72.G
Deformation isomonodromic 253.E
Deformation isospectral 387.C
Deformation of a scheme over a connected scheme 16.W
Deformation of a surface 110.A
Deformation projective (between surfaces) 110.B
Deformation retract 202.D
Deformation retract neighborhood 202.D
Deformation retract strong 202.D
Degeneracy (of energy eigenvalues) 351.H
Degeneracy index 17.C
Degeneracy operator (in a semisimphcial complex) 70.E
| Degeneracy, set of (of a holomorphic mapping between analytic spaces) 23.C
Degenerate (critical point) 106.L 279.B
Degenerate (eigenvalue) 390.A 390.B
Degenerate (mapping) 208.B
Degenerate (quadratic surface) 350.B
Degenerate (simplex) 70.E
Degenerate kernel 217.F
Degenerate module 118.D
Degenerate series (of unitary representations of a complex semisimple Lie group) 437.W
Degenerate series complementary (of unitary representations of a complex semisimple Lie group) 437.W
Degenerate totally 234.B
Degree (of a 0-cycle on an algebraic variety) 16.M
Degree (of a central simple algebra) 29.E
Degree (of a divisor class) 11.D
Degree (of a divisor of an algebraic curve) 9.C
Degree (of a graph) 186.B
Degree (of a Jordan algebra) 231.B
Degree (of a linear representation) 362.D
Degree (of a matrix representation) 362.D
Degree (of a permutation representation) 362.B
Degree (of a polynomial) 337.A
Degree (of a prime divisor) 9.D
Degree (of a rational homomorphism) 3.C
Degree (of a representation of a Lie algebra) 248.B
Degree (of a representation of a Lie group) 249.O
Degree (of a square matrix) 269.A
Degree (of a term of a polynomial) 337.B
Degree (of a valuation) 439.I
Degree (of an algebraic element) 149.F
Degree (of an algebraic equation) 10.A
Degree (of an algebraic variety) 16.G
Degree (of an angle) 139.D
Degree (of an element with respect to a prime ideal of a Dedekind domain) 439.F
Degree (of an extension) 149.F
Degree (of an ordinary differential equation) 313.A
Degree complementary (of a spectral sequence) 200.J
Degree filtration 200.J
Degree formal (of a unitary representation) 437.M
Degree in- 186.B
Degree k, holomorphic differential forms of 72.A
Degree k, tensor space of 256.I
Degree Leray — Schauder 286.D
Degree local, of mapping 99.B
Degree mapping 99.A
Degree n, alternating group of 151.G
Degree n, component of 200.B
Degree n, general linear group of 60.B
Degree n, projective general linear group of 60.B
Degree n, Siegel modular function of 32.F
Degree n, Siegel modular group of 32.F
Degree n, Siegel space of 32.F
Degree n, Siegel upper half-space of 32.F
Degree n, special linear group of 60.B
Degree n, symmetric group of 151 .G
Degree of a prime divisor of an algebraic function field of dimension 1 9.D
Degree of covering (of a nonsingular curve) 9.I
Degree of freedom (of error sum of squares) 403.E
Degree of freedom (of sampling distributions) 374.B
Degree of freedom (of the dynamical system) 271.F
Degree of mapping 99. A
Degree of ramification (of a branch point) 367.B
Degree of recursive unsolvability 97
Degree of symmetry 431.D
Degree of the point 99.D
Degree of transcendency (of a field extension) 149.K
Degree of unsolvability 97
Degree out- 186.B
Degree p, contravariant tensor of 256.J
Degree q, covariant tensor of 256.J
Degree r, differential form of 105.Q
Degree r, differential form of (on an algebraic variety) 16.O
Degree r, mean of (of a function with respect to a weight function) 211.C
Degree relative (of a finite extension) 257.D
Degree relative (of a prime ideal over a field) 14.I
Degree total (of a spectral sequence) 200.J
Degree transcendence (of a field extension) 149.K
Dehn lemma (on 3-manifolds) 65.E
Dehn, Max(1878-1952) 65.E 155.F 196
Dejon — Nickel method 301.G
Dejon, Bruno F.(1930-) 301.G 301.r
Dekkers, A.J. NTR
Delaunay curve 93.H
Delaunay, Charles Eugene(1816-1872) 93.H
Delay convention, perfect 51.F
Delay-differential equation 163.A
Delayed recurrent event 260.C
Deleanu, Aristide(1932-) 52.r
Delens, Paul Clement(1889-) 110.r
Deligne, Pierre(1944-) 9.r 12.B 16.V 16.r 32.D 118.B 418.r 428.H 450.A 450.G 450.H 450.J 450.M 450.Q 450.S App.B Table
Dellacherie, Claude(1943-) 22.r 261.r 262.r 407.B 407.r
Delos problem (in geometric construction) 179.A
Delta function, Dirac App. A Table
Delta, Kronecker 269.A App. Table
Deltheil, Robert 218.r
Demazure, Michel(1937-) 13.r 16.I 16.Z 16.r
Deming, William Edwards(1900-) 280.J 373.F 373.r
Democritus(c.460-c.370 B.C.) 187
Demography 40.D
Denes, Jozsef(1932-) 241.r
Denjoy integrable in the wider sense 100.D
Denjoy integrals 100
Denjoy integrals in the restricted sense 100.D
Denjoy — Carleman condition 168.B
Denjoy — Luzin theorem 159.I
Denjoy, Arnaud(1884-1974) 58.F 79.D 100.A 100.D 126.I 154.D 154.H 154.r 159.I 168.B 429.D
Denker, Manfred(1944-) 136.H
Denominator, partial (of an infinite continued fraction) 83.A
Dense (set) 425.N
Dense (totally ordered set) 311.B
Dense in itself 425.O
Dense locally 154.D
Dense nowhere 425.N
Dense relatively 126.E
Dense Zariski 16.A
Denseness of rational numbers 355.B
Density (of a set of prime ideals) 14.S
Density (of a subset of integers) 4.A
Density (on a maximal torus) 248.Y
Density 4-current 150.B
Density angular momentum 150.B
Density beta 397.D
Density bivariate normal 397.I
Density conditional 397.I
Density cospectral 397.N
Density electric flux 130.A
Density energy 195.B
Density free Lagrangian 150.B
Density function 397.D
Density function bispectral 421.C
Density function marginal 397.I
Density function normal 397.D
Density function rational spectral 176.F
Density gamma 397.D
Density joint 397.I
Density kinetic 218. A
Density Lagrangian 150.B
Density magnetic flux 130.A
Density matrix 351.B
Density posterior 401.B
Density prior 401.B
Density probability 341.D
Density sojourn time 45.G
Density theorem (on discrete subgroups of a Lie group) 122.F
Density theorem Chebotarev 14.S
Density theorem Kaplansky 308.C
Density theorem Lebesgue 100.B
Density theorem von Neumann 308.C
Density, point of (of a measurable set of the real line) 100.B
Deny, Jacques(1916-) 338.M—P 338.r
Dependence, domain of 325.B
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -field
-field  -function, rapidly
-function, rapidly 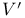 (for a rational mapping)
(for a rational mapping) 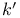 (for an algebraic variety)
(for an algebraic variety)