|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Frame(s) moving 90.B 111.C 417.B
Frame(s) natural moving 417.B
Frame(s) normal 110.B
Frame(s) of order 0 110.C
Frame(s) of order 1 110.B 110.C
Frame(s) of order 2 110.B 110.C
Frame(s) of order 3 110.B 110.C
Frame(s) of order 4 110.B
Frame(s) orthogonal (in a Euclidean space) 111.B 139.E
Frame(s) orthogonal k- (in 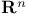 ) 199.B ) 199.B
Frame(s) orthogonal moving 417.D
Frame(s) projective 343.C
Frame(s) Stiefel manifold of k- 199.B
Frame(s) stochastic moving 406.G
Frame(s) tangent r- 105.H
Frame, J.S. App.B Table
Framed link 114.L
Framing 114.L
Francis, J.G.F. 298.F
Frank, Philipp(1884-1966) 129.r
Frankel, Theodore T.(1929-) 364.D
Franklin, Philip(1898-1965) 157.A 157.E
Franklin, Stanley P.(1931-) 425.CC
Franks, John M.(1943-) 126.J 126.K
Franz, Wolfgang(1905-) 91.r 337.F
Fraser, Donald Alexander Stuart(1925-) 396.r 401.r
Frautschi, Steven Clark(1933-) 386.r
Frechet axiom 425.Q
Frechet curve 246.A
Frechet derivative 286.E
Frechet differentiable function 286.E
Frechet differential 286.E
Frechet distance (between surfaces) 246.I
Frechet L-space 87.K
Frechet manifold 286.K
Frechet space (quasinormed space) 37.O
Frechet space (topological linear space) 424.I
Frechet space (topological space) 425.CC
Frechet space in the sense of Banach 37.O
Frechet space in the sense of Bourbaki 424.I
Frechet space locally convex 424.I
Frechet surface 246.I
Frechet — Uryson space 425.CC
Frechet, Rene Maurice(1878-1973) 37.O 87.K 87.r 117.H 246.A 246.I 273.A 273.r 286.E 286.K 424.I 425.Q 425.S 425.CC 425.r 426
Fredholm alternative theorem 68.E 217.F
Fredholm determinant 217.E
Fredholm first minor 217.E
Fredholm formula 68.L
Fredholm integral equation 217.A
Fredholm integral equation of the first kind 217. A
Fredholm integral equation of the second kind 217.A
Fredholm integral equation of the third kind 217.A
Fredholm mapping 286.E
Fredholm operator 68.F 251.D
Fredholm operator (in the sense of Grothendieck) 68.K
Fredholm rth minor 217.E
Fredholm type, integral equation of 217.A
Fredholm type, integrodifferential equation of 222.A
Fredholm, Erik Ivar(1866-1927) 20 68.A 68.E 68.F 68.K 68.L 120.A 162 217.A 217.E 217.F 217.r 222.A 251.D 286.E 339.D
Free 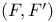 -(oriented G-manifold) 431.E -(oriented G-manifold) 431.E
Free (discontinuous group) 122.A
Free Abelian group 2.C
Free additive group 2.E
Free derivative 235.C
Free Dirac field 377.C
Free distribution- 371. A
Free energy 340.B 402.G
Free energy Gibbs 419.C
Free energy Helmholtz 419.C
Free energy mean 340.B 402.G
Free F- (oriented G-manifold) 431.E
Free fields 150.A
Free grammar, context- 31.D
Free groups 161
Free Hamiltonian 351.D
Free homotopy 202.B
Free Lagrangian density 150.B
Free module 277.G
Free product (of groups) 190.M
Free scalar field 377.C
Free semigroup 161. A
Free special Jordan algebra 231.A
Free vacuum vector 150.C
Free variable 411.C
Free vector 442.A
Freedman, David A.(1938-) 250.r
Freedman, Michael Hartley(1951-) 114.K 114.r
Freedom asymptotic 361.B
Freedom degrees of (of a dynamical system) 271.F
Freedom n degrees of (sampling distribution) 374.B 374.C
Freely act 122.A 431.A
Frege, Friedrich Ludwig Gottlob(1848-1925) 156.B 411.A 411.r
Freitag, Eberhard(1942-) 32.F
French empiricism 156.C
Frenet formula 111.D
Frenet frame 110.A 111.D
Frenet — Serret formulas (on curves) 111.D App. Table
Frenet, Jean-Frederic(1816-1900) 110.A 111.D App.A Table
Frequency (of a translational flow) 126.L 136.G
Frequency (of a wave) 446
Frequency (of an oscillation) 318.A
Frequency (of samples) 396.C 397.B
Frequency angular (of a wave) 446
Frequency circular (of a simple harmonic motion) 318.B
Frequency distribution 397.B
Frequency function 397.D
Frequency relative (of samples) 396.C
Frequency response function 421.E
Fresnel integral 167.D App. Tables 19.II
Fresnel, Augustin Jean(1788-1827) 167.D App.A Tables 19.II
Freudenthal theorem 202.U
Freudenthal, Hans(1905-) 162 178.F 202.A 202.U 202.r 248.r 249.r 265 310.A 310.D
Freyd, Peter John(1936-) 52.r 200.r
Fricke, Robert(1861-1930) 32.r 73.r 122.r 233.r 234.r
Friedberg, Richard Michael(1935-) 356.D
Friedman, Avner(1932-) 108.A 108.B 115.D 286.r 320.r 322.r 327.r 406.r 440.r
Friedman, James W. 173.E
Friedman, Lawrence 307.r
Friedman, Nathaniel A.(1938-) 136.E 136.r
Friedrichs extension 112.I 251.I
Friedrichs scheme 304.F
Friedrichs theorem 323.H 326.D
Friedrichs, Kurt Otto(1901-83) 112.D 112.I 112.S 125.A 162 204.G 205.r 252.r 300.r 304.F 323.H 323.r 325.G 325.r 326.D 331.A 345.A 351.K 375.A
Frieze group 92.F
Fristedt, Bert(1937-) 5.r
Frobenius algebra 29.H
Frobenius algebra quasi- 29.H
Frobenius automorphism (of a prime ideal) 14.K
Frobenius group 151.H
Frobenius integrability condition 154.B
Frobenius method App. A Table
Frobenius morphism 450.P
Frobenius substitution (of a prime ideal) 14.K
Frobenius theorem (on Abelian varieties) 3.D
Frobenius theorem (on matrices with nonnegative entries) 269.N
Frobenius theorem (on polynomials of a matrix) 390.B
Frobenius theorem (on representations of finite groups) 362.G
Frobenius theorem (on total differential equations and on foliations) 154.B 286.H 428.D
Frobenius theorem, Perron — 310.H
Frobenius, Ferdinand Georg(1849-1917) 1.r 2.B 3.A 3.D 3.N 14.K 29.H 107.A 145 151.H 154.B 190.Q 190.r 191.B 257.D 267 269.I 269.N 280.F 286.H 297.I 310.H 362.E 362.G 390.B 428.A 428.D 437.EE 450.P App.A Table
Froehlich, Albrecht(1916-) 14.r 59.r
Froehlich, Jiirg M.(1946-) 402.G
Froissart bound 386.B
Froissart — Martin bound 386.B
Froissart, Marcel(1934-) 146.A 386.B
Frolik, Zdenek(1933-) 425.Y 425.CC 436.r
Fronsdal, Christian(1931-) 132.r
Front set, analytic wave 274.D
Front set, wave 274.B 345.A
Frontier point (of a subset) 425.N
| Frostman maximum principle 338.C
Frostman, Otto Albin(1907-1977) 48.A 48.G 120.D 338.C 338.r
Froude number 116.B
Froude, William(1810-1879) 116.B
Fu, James Chuan(1937-) 399.M
Fubini theorem 221.E
Fubini, Guido(1879-1943) 109 110.B 110.r 221.E 270.L
Fubini, Sergio Piero(1928-) 132.r
Fuchs, Immanuel Lazarus(1833-1902) 32.B 107.A 119.r 122.C 178.F 234.B 288.B App.A Table
Fuchs, Ladislas 2.r
Fuchs, Maximilian Ernst Richard(1873-) 253.A 253.E 288.D
Fuchs, Wolfgang Heinrich(1915-) 17.D 272.K 272.r
Fuchsian form of weight k (or of dimension - k) 32.B
Fuchsian function 32.B
Fuchsian group 122.C
Fuchsian group of the first kind 122.C
Fuchsian group of the second kind 122.C
Fuchsian relation 253.A App. Table
Fuchsian type (visibility manifold) 178.F
Fuchsian type, equation of 253.A
Fuchsoid group 122.C
Fucter, Karl Rudolf(1880-1950) 73.r
Fuerstenberg, Hillel 136.C 136.H
Fuglede, Bent(1925-) 48.H 143.B 338.E
Fujii, Hiroshi(1940-) 304.D
Fujiki, Akira(1947-) 23.G 72.H 232.C
Fujikoshi, Yasunori(1942-) 280.r
Fujimagari, Tetsuo(1943-) 44.E
Fujimoto, Hirotaka(1937-) 21.M 21.N
Fujisaki, Genjiro(1930-) 6.F 450.L
Fujisaki, Masatoshi(1943-) 86.E 405.r
Fujisawa, Rikitaro(1861-1933) 267
Fujishige Satoru(1947-) 66.r 281.r
Fujita, Hiroshi(1928-) 204.B—D 304.r 378.J
Fujita, Takao(1949-) 9.r 15.H 72.I
FujiTe, Tatuo(1930-) 143.r
Fujiwara, Daisuke(1939-) 323.H 345.B
Fujiwara, Masahiko(1943-) 118.C 118.D
Fujiwara, Matsusaburo(1881-1946) 89.E 230.* 280.r 240.B App.A Table
Fukamiya, Masanori(1912-) 162
Fuks cohomology, Gel’fand— 105.AA
Fuks, Boris Abramovich(1907-1975) 21.r 198.r
Fuks, Dmitrii Borisovich 105.AA 105.r 154.G
Fukushima Masatoshi(1935-) 115.C 261.r
Fulkerson, Delbert Ray(1924-76) 376.r
Full discrete approximation 304.B
Full embedding theorem (of an Abelian category) 52.N
Full group 136.F 258.A
Full homogeneous Lorentz group 258.A
Full inhomogeneous Lorentz group 258.A
Full international notation 92.E
Full linear group 60.B
Full matrix algebra 269.B
Full Poincare group 258.A
Full subcategory 52.A
Fuller, Francis Brock 126.G 126.N
Fully complete (locally convex space) 424.Y
Fully faithful functor 52.H
Fully normal space 425.X
Fully transitive 92.C
Fulton and Hansen, general connectedness theorem of 16.I
Fulton, William(1939-) 9.r 16.I 366.E 366.r 418.r
Function algebra 164.A
Function element 198.I 339.A
Function element in the wider sense 198.O
Function element inverse 198.L
Function field (of an algebraic curve over a field) 9.C
Function field (of an algebraic variety) 16.A
Function field Abelian 3.J
Function field algebraic, in n variables 149.K
Function field algebraic, over k of dimension 1 9.D
Function field algebraic, over k of transcendence degree 1 9.D
Function field elliptic 9.D
Function field rational, in n variables 149.K
Function group 234.A
Function matrix rational 86.D
Function matrix transfer 86.B
Function space(s) 168 435.D
Function space(s) test 125.S
Function symbol 411.H
Function variable 411.H
Function(s) 165 381.C
Function(s)  -, in a -, in a  -manifold 105.G -manifold 105.G
Function(s)  - (of many variables) 58.B - (of many variables) 58.B
Function(s)  - , slowly increasing 125.O - , slowly increasing 125.O
Function(s)  -excessive 261.D -excessive 261.D
Function(s)  - 391.L - 391.L
Function(s)  - 32.C - 32.C
Function(s) 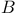 -measurable 270.J -measurable 270.J
Function(s) 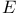 - 46.C - 46.C
Function(s)  -conformal 352.B -conformal 352.B
Function(s)  -, of Weierstrass 134.F App. Table -, of Weierstrass 134.F App. Table
Function(s)  - 150.D - 150.D
Function(s) 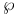 -, of Weierstrass 134.F App. Table -, of Weierstrass 134.F App. Table
Function(s) Abelian 3.J
Function(s) absolutely integrable 214.E
Function(s) additive interval 380.B
Function(s) additive set 380.C
Function(s) admissible 46.A 304.B
Function(s) Ahlfors 43.G 77.E
Function(s) algebraic 11.A
Function(s) almost periodic 18
Function(s) almost periodic, in the sense of Bohr 18.B
Function(s) almost periodic, on a group 18.C
Function(s) almost periodic, with respect to p 18.C
Function(s) alternating 337.I
Function(s) amplitude (of a Fourier integral operator) 274.C 345.B
Function(s) analytic almost periodic 18.D
Function(s) analytic operator 37.K
Function(s) Anger 39.G App. Table
Function(s) Appell hypergeometric, of two variables 206.D App. Table
Function(s) argument 46.A
Function(s) arithmetic 295.A
Function(s) Artin — Hasse 257.H
Function(s) associated Legendre 383.C App. Table
Function(s) asymptotically developable 30.A
Function(s) automorphic 32
Function(s) automorphic, with respect to  32.A 32.A
Function(s) b- 125.EE 418.H
Function(s) Baire 84.D
Function(s) Barnes extended hypergeometric 206.C App. Table
Function(s) base 304.B
Function(s) Bellman 127.G
Function(s) Bergman kernel 188.G
Function(s) Bessel 39 App. Table
Function(s) beta 174.C App. Table
Function(s) bispectral density 421.C
Function(s) Borel measurable 270.J
Function(s) boundary 160.E
Function(s) bounded 43.A
Function(s) Busemann 178.F
Function(s) canonical (on a nonsingular curve) 9.E
Function(s) characteristic (for an optical system) 180.C
Function(s) characteristic (of a density function) 397.G
Function(s) characteristic (of a graded A-module) 369.F
Function(s) characteristic (of a meromorphic function) 272.B
Function(s) characteristic (of a probability measure) 341.C
Function(s) characteristic (of a subset) 381.C
Function(s) characteristic (of an n-person cooperative game) 173.D
Function(s) characteristic operator 251.N
Function(s) Chebyshev App. A Table
Function(s) Chebyshev q- 19.G App. Table
Function(s) choice 33.B 34.A
Function(s) circular 131.F 432.A
Function(s) class (on a compact group) 69.B
Function(s) cn App. A Table
Function(s) completely additive set 380.C
Function(s) completely monotonic 240.E 240.K
Function(s) completely multiplicative number-theoretic 295.B
Function(s) complex 165.B
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
)  -(oriented G-manifold)
-(oriented G-manifold)  -, in a
-, in a  -manifold
-manifold -excessive
-excessive  -
-  -
-  -measurable
-measurable  -
-  -conformal
-conformal  -, of Weierstrass
-, of Weierstrass  -
-  -, of Weierstrass
-, of Weierstrass 