|
|
 |
| Авторизация |
|
|
|
| Поиск по указателям |
|
|
|
|
|
|
|
 |
|
|
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
|
| Предметный указатель |
Commutor 368.E
Comonad 200.Q
Compact  -manifold 105.D
Compact (continuous mapping) 286.D
Compact (kernel distribution) 125.L
Compact (linear operator) 68.B
Compact (topological space) 425.S
Compact algebraic group, k- 13.G
Compact cardinal number strongly 33.E
Compact cardinal number weakly 33.E
Compact complex manifolds, family of 72.G
Compact element (of a topological Abelian group) 422.F
Compact foliation 154.H
Compact form (of a complex semisimple Lie algebra) 248.P
Compact group 69.A
Compact homotopy class 286.D
Compact leaf 154.D
Compact linearly 422.L
Compact locally linearly 422.L
Compact metric space 273.F
Compact open  topology 279.C
Compact operators 68
Compact real Lie algebra 248.P
Compact real simple Lie algebra classical 248.T
Compact real simple Lie algebra exceptional 248.T
Compact real- 425.BB
Compact relatively (linear operator) 331.B
Compact relatively (maximum likelihood method) 399.M
Compact relatively (subset) 273.F 425.S
Compact sequentially 425.S
Compact set 425.S
Compact set in a metric space 273.F
Compact set relatively 399.M 425.S
Compact set, uniform convergence on 435.C
Compact simple Lie group classical 249.L
Compact simple Lie group exceptional 249.L
Compact space 425.S
Compact space  - 425.V
Compact space countably 425.S
Compact space locally 425.V
Compact space real- 425.BB
Compact space sequentially 425.S
Compact space uniformly locally 425.V
Compact support (singular q-cochain) 201.P
Compact type (symmetric Riemannian homogeneous space) 412.D
Compact uniformly locally 425.V
Compact weakly (linear operator) 68.M
Compact, - 425.V
Compact, T- 68.F 331.B
Compact-open topology 279.C 435.D
Compactification (of a complex manifold) 72.K
Compactification (of a Hausdorff space) 207.A
Compactification (of a topological space) 425.T
Compactifying (kernel) 125.L
Compactifying Aleksandrov 207.C
Compactifying Bohr 18.H
Compactifying F- 207.C
Compactifying Kerekjarto — Stoilow 207.C
Compactifying Kuramochi 207.C
Compactifying Martin 207.C
Compactifying one-point (of a topological space) 425.T
Compactifying Royden 207.C
Compactifying Stone — Cech 207.C425.T
Compactifying Wiener 207.C
Compactifying, resolutive 207.B
Compactness theorem (in model theory) 276.E
Compactum, dyadic 79.D
Companion matrix 301.I
Comparability theorem for cardinal numbers 49.B
Comparison test (for convergence) 379.B
Comparison theorem (in the theory of differential equations) 316.E
Comparison theorem metric 178.A
Comparison theorem triangle 178.A
Comparison, paired 346.C
compass 179.A
Compatible with -structure 114.B
Compatible with a triangulation (a -structure) 114.C
Compatible with composition 409.C
Compatible with operation (of an operator domain) 277.C
Compatible with operations in a linear space 256.F
Compatible with the multiplication of a group 190.C
Compatible with topology 436.H
Compiler 75.C
Complement (in lattice theory) 42.A 243.E
Complement (in set theory) 381.B
Complement (of a decision problem) 71.B
Complement conjecture, knot 235.B
Complement orthogonal (of a subset of a Hilbert space) 197.E
Complement relative (of two sets) 381.B
Complement theorem 382.B
Complement theorem Chapman’s 382.B
Complementary analytic set 22.A
Complementary degenerate series 437.W
Complementary degree 200.J
Complementary event 342.B
Complementary law of reciprocity 14.O
Complementary law of the Jacobi symbol 297.I
Complementary law of the Legendre symbol, first 297.I
Complementary law of the Legendre symbol, second 297.I
Complementary modulus (in Jacobi elliptic functions) 134.J App. Table
Complementary series 437.W
Complementary set 381.B
Complementary slackness, Tucker theorem on 255.B
Complementary submodule 277.H
Complementary subspace (of a linear subspace) 256.F
Complementation, law of (in a Boolean algebra) 42.A
Complemented (Banach space) 37.N
Complemented lattice 243.E
Completable topological group 423.H
Complete - (vector lattice) 310.C
Complete -field 396.E
Complete -field boundedly 396.E
Complete (Abelian p-group) 2.D
Complete (algebraic variety) 16.D
Complete (increasing family of -algebras) 407.B
Complete (logical system) 276.D
Complete (metric space) 273.J
Complete (ordinary differential equation) 126.C
Complete (predicate) 356.H
Complete (recursively enumerable set) 356.D
Complete (set of closed formulas) 276.F
Complete (statistics) 396.E
Complete (system of axioms) 35.B
Complete (system of orthogonal functions) 317.A
Complete (topological group) 423.H
Complete (uniform space) 436.G
Complete (valuation) 439.D
Complete (vector lattice) 310.C
Complete (wave operator) 375.B
Complete (Zariski ring) 284.C
Complete accumulation point 425.O
Complete additive group 2.E
Complete additivity (of a measure) 270.D
Complete additivity (of the Lebesgue integral) 221.C
Complete additivity theorem, Pettis 443.G
Complete analytic space, K- 23.F
Complete at o (in the theory of deformation) 72.G
Complete B-(locally convex space) 424.X
Complete bipartite graph 186.C
Complete blocks 102.B
Complete capture 420.D
Complete class 398.B
Complete class essentially 398.B
Complete class minimal 398.B
Complete class theorems 398.D
Complete cohomology theory 200.N
Complete distributive law (in a lattice-ordered group) 243.G
Complete elliptic integral App. A Table
Complete elliptic integral of the first kind 134.B
Complete elliptic integral of the second kind 134.C
| Complete form, theorem on 356.H
Complete free resolution (of  ) 200.N
Complete fully (locally convex space) 424.X
Complete graph 186.C
Complete holomorphically (domain) 21.F
Complete hyperbolic manifolds 21.O
Complete induction 294.B
Complete integrability condition 428.C
Complete intersection 16.A
Complete lattice 243.D
Complete lattice - 243.D
Complete lattice conditionally 243.D
Complete linear system defined by a divisor 16.N
Complete linear system on an algebraic curve 9.C
Complete linear system on an algebraic variety 16.N
Complete local ring 284.D
Complete local ring, structure theorem of 284.D
Complete manifold, weakly 1- 21.L
Complete mapping 241.B
Complete maximum principle 338.M
Complete measure 270.D
Complete measure space 270.D
Complete metric space 273.J
Complete NP- 71.E
Complete observation 405.C.D
Complete orthogonal system 217.G
Complete orthonormal set (Hilbert space) 197.C
Complete orthonormal system 217.G
Complete orthonormal system of fundamental functions 217.G
Complete pivoting 302.B
Complete predicate 356.H
Complete product measure space 270.H
Complete quadrangle 343.C
Complete quasi- (locally convex space) 424.F
Complete reducibility theorem, Poincare 3.C
Complete Reinhardt domain 21.B
Complete residue system modulo m 297.G
Complete ring (with respect to an ideal I) 16.X
Complete scheme, k- 16.E
Complete set 241.B
Complete solution (of partial differential equations) 320.C
Complete space 436.G
Complete space Cech 425.T 436.I
Complete space Dieudonne 436.I
Complete space holomorphically 23.F
Complete space topologically 436.I
Complete system of axioms 35.B
Complete system of independent linear partial differential equations 324.C
Complete system of inhomogeneous partial differential equations 428.C
Complete system of nonlinear partial differential equations 428.C
Complete valuation 439.D
Complete vector lattice 310.C
Complete vector lattice - 310.C
Complete weakly 1-, manifold 21.L
Complete Zariski ring 284.C
Completely additive (arithmetic function) 295.B
Completely additive (measure) 270.D 270.E
Completely additive (vector measure) 443.G
Completely additive class 270.B
Completely additive set function 380.C
Completely continuous operator 68.B
Completely integrable 154.B
Completely integrable (system of indepsndent 1- forms) 428.D
Completely integrally closed (ring) 67.I
Completely monotonic function 240.E 240.K
Completely multiplicative number-theoretic function 295.B
Completely nonunitary 251.M
Completely normal space 425.Q
Completely passive 402.G
Completely positive 36.H
Completely positive entropy 136.E
Completely primary ring 368.H
Completely randomized design 102.A
Completely reducible A-module 277.H
Completely reducible group 190.L
Completely reducible linear representation 362.C
Completely regular space 425.Q
Completely unstable flow 126.E
Completeness (for a Cartan connection) 80.N
Completeness (of a logical system) 276.D
Completeness (of the predicate calculus) 411.J
Completeness asymptotic 150.D
Completeness NP- 71.E
Completeness of real numbers 294.E 355.B
Completeness of scattering states 150.D 386.B
Completeness theorem Goedel 411.J
Completeness, theorem of (in geometry) 155.B
Completion 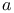 -adic (of an R-module) 284.B
Completion  - 270.D
Completion of a  -topological group 423.H
Completion of a field (with respect to a valuation) 439.D
Completion of a measure space 270.D
Completion of a metric space 273.J
Completion of a ring along an ideal 16.X
Completion of a uniform space 436.G
Completion of a valuation 439.D
Completion of a valuation ring (of a valuation) 439.D
Completion of an ordered set 243.D
Completion of Spec(A) along V(I) 16.X
COMPLEX 362.F
Complex algebraic variety 16.T
Complex analytic fiber bundle 147.O
Complex analytic function 198.H
Complex analytic manifold 72.A
Complex analytic structure (in a complex manifold) 72.A
Complex analytic submanifold 72.A
Complex cobordism group 114.H
Complex cobordism ring 114.H
Complex conjugate bundle 147.F
Complex conjugate representation 362.F
Complex dimension (of a complex manifold) 72.A
Complex form (of a real Lie algebra) 248.P
Complex form (on a Fourier series) 159.A
Complex function 165.B
Complex Gaussian 176.B
Complex Gaussian process 176.C
Complex Gaussian random variable 176.B
Complex Gaussian system 176.B
Complex Grassmann manifold 199.B
Complex group (over a field) 60.L
Complex Hermitian homogeneous space 199.A
Complex Hilbert space 197.B
Complex interpolation space 224.C
Complex Lie algebra 248.A
Complex Lie algebra of a complex Lie group 249.M
Complex Lie group 249.A
Complex line bundle 72.F
Complex line bundle determined by a divisor 72.F
Complex linear space 256.A
Complex manifold(s) 72
Complex manifold(s) almost 72.B
Complex manifold(s) compact, family of 72.G
Complex manifold(s) isomorphic 72.A
Complex manifold(s) stably almost 114.H
Complex manifold(s) weakly almost 114.H
Complex multiplication 73
Complex number plane 74.C
complex numbers 74.A 294.F
Complex numbersconjugate 74.A
Complex of lines 110.B
Complex orthogonal group 60.I
Complex orthogonal matrix 269.J
Complex plane 74.C
Complex projective space 343.E
Complex projective space infinite-dimensional 56
Complex quadratic form 348.A 348.B
Complex representation (of a Lie group) 249.O
Complex simple Lie algebra classical 248.S
Complex simple Lie algebra exceptional 248.S
Complex simple Lie group classical 249.M
|
|
|
| Реклама |
|
|
|
|
|
О проекте