|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Conductor (of Hecke L-functions) 450.E
Conductor p-(of norm-residue) 14.P
Conductor with a group character 450.G
Conductor-ramification theorem (in class field theory) 59.C
Cone (in a projective space) 343. E
Cone (of a PL embedding) 65.D
Cone (of a simplicial complex) 70.C
Cone (over a space) 202.E
Cone asymptotic 350.B
Cone circular 78.A 111.I
Cone conjugate convex 89.F
Cone convex 89.F
Cone convex polyhedral 89.F
Cone dual convex 89.F
Cone extension (of a PL embedding) 65.D
Cone future 258.A
Cone light 258.A
Cone Mach 205.B
Cone mapping 202.E
Cone natural positive 308.K.
Cone oblique circular 350.B
Cone past 258.A
Cone quadric 350.B
Cone reduced (of a topological space) 202.F
Cone reduced mapping 202.F
Cone regular 384.A
Cone right circular 350.B
Cone self-dual regular 384.E
Cone side 258.A
Confidence coefficient 399.Q
Confidence interval 399.Q
Confidence level 399.Q
Confidence limits 399.Q
Confidence region 399.Q
Confidence region invariance of 399.Q
Confidence region unbiased 399.Q
Confidence region uniformly most powerful 399.Q
Confidence region uniformly most powerful unbiased 399.Q
Configuration central 420.B
Configuration Pascal 78.K
Configuration space 126.L 402.G
Confluent differential equation 167.A
Confluent hypergeometric differential equation 167.A App. Table
Confluent type, function of 167.A
Confluent type, hypergeometric function of 167.A App. Table
Confocal central conies, family of 78.H
Confocal parabolas, family of 78.H
Confocal quadrics, family of 350.E
conformal 77.A
Conformal arc element 110.D
Conformal connection 80.P
Conformal correspondence (between surfaces) 111.I
Conformal curvature 110.D
Conformal curvature tensor, Weyl 80.P App. Table
Conformal differential geometry 110.D
Conformal function,  - 352.B - 352.B
Conformal geometry 76.A
Conformal invariant 77.E
Conformal mapping 198.A App. Table
Conformal mapping extremal quasi- 352.C
Conformal mapping generalized 246.I
Conformal mapping quasi- 352
Conformal space 76.A
Conformal structure 191.B
Conformal structure (on a Riemann surface) 367.A
Conformal torsion 110.D
Conformal transformation 80.P 364.F
Conformalalmost 275.C
Conformally equivalent 77.A 367.A 191.B
Conformally fiat 191.B
Conformally flat space App. A Table
Conforto, Fabio(1909-1954) 3.r
Confounded partially (with blocks) 102.J
Confounded with blocks 102.J
Congruence (in geometry) 155.B
Congruence (in number theory) 297.G
Congruence axiom (of geometry) 155.B
Congruence classes modulo m*, group of 14.H
Congruence linear (in projective geometry) 343.E
Congruence multiplicative 14.H
Congruence of lines 110.B
Congruence subgroup (of a modular group) 122.D
Congruence subgroup principal, of level N 122.D
Congruence zeta function 450.P
Congruent (figures) 139.C
Congruent (segment) 155.B
Congruent affinely 7.E
Congruent in the Erlangen program 137
Congruent modulo m 297.G
Congruent transformation(s) 139.B
Congruent transformation(s), group of 285.C
Conic Lagrange manifold 274.C 345.B
Conic section(s) 78.A
Conic section(s), canonical form of the equation of 78.C
Conic section(s), equation of 78.C
Conic(s) 78.A
Conic(s) central 78.C
Conic(s) focal (of a quadric) 350.E
Conic(s), pencil of 343.E
Conical function App. A Table
Conical hypersurface, quadric 350.G
Conical surface 111.I
Conical surface quadric 350.B
Conjecture 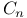 (on Kodaira dimension) 72.H (on Kodaira dimension) 72.H
Conjecture Adams (on J-homomorphisms) 237.I
Conjecture annulus (on combinatorial manifolds) 65.C
Conjecture Artin (on Artin L-functions) 450.G
Conjecture Bieberbach (on univalent functions) 438.C
Conjecture Birch — Swinnerton — Dyer (on L-functions of elliptic curves) 118.D 450.S
Conjecture Burnside (on finite groups) 151 .D
Conjecture entropy 126.K
Conjecture four color 186.T
Conjecture fundamental (in topology) 70.C
Conjecture general knot 235.B
Conjecture generalized Poincare 65.C
Conjecture Hasse (on Hasse zeta function) 450.S
Conjecture Hodge (on cycles on algebraic varieties) 450.S
Conjecture Iwasawa main (on p-adic L-functions) 450.J
Conjecture knot complement 235.B
Conjecture Leopoldt (on p-adic L-functions) 450.J
Conjecture Mordell (on Diophantine equations) 118.E
Conjecture Poincare (on a characterization of spheres) 65.C
Conjecture property P- (on knot groups) 235.B
Conjecture Ramanujan (on automorphic functions) 32.D
Conjecture Ramanujan — Petersson (on Hecke operators) 32.D
Conjecture Sato (on Hasse zeta functions) 450.S
Conjecture Schreier (on simple groups) 151.I
Conjecture Seifert (on vector fields) 126.K 154.D
Conjecture Smith (on knot theory) 235.E
Conjecture stability 126.J
Conjecture Taniyama — Weil (on L-functions of elliptic curves) 450.S
Conjecture Tate (on Hasse  -functions) 450.S -functions) 450.S
Conjecture topological 126.B
Conjecture unknotting 235.E
Conjecture Vandiver (on the class number of cyclotomic fields) 14.L
Conjecture Weil (on congruence zeta functions) 450.Q
Conjugacy  - 126.B - 126.B
Conjugacy class (of an element of a group) 190.C
Conjugate  - 126.B - 126.B
Conjugate  - 126.H - 126.H
Conjugate (CG method) 302.D
Conjugate (diameter) 78.G
Conjugate (element) 149.J
Conjugate (point in a geodesic) 178.A
Conjugate (point in a projective space) 343.E
Conjugate (quaternion) 29.D
Conjugate (subset) 190.C
Conjugate (with respect to a quadric surface) 350.C
Conjugate axis (of a hyperbola) 78.C
Conjugate complex number 74.A
| Conjugate convex cone 89.F
Conjugate differential (on Riemann surface) 367.H
Conjugate exponent 168.C
Conjugate field 149.J 377.C
Conjugate Fourier integral 160.D
Conjugate function 159.E 160.D
Conjugate gradient (CG) method 302.D
Conjugate harmonic (in projective geometry) 343.D
Conjugate harmonic function 193.C
Conjugate hyperbola 78.E
Conjugate ideal (of a fractional ideal) 14.I
Conjugate operator (in Banach spaces) 37.D
Conjugate operator (of a differential operator) 125.F
Conjugate operator (of a linear operator) 251.D
Conjugate planes (with respect to a quadric surface) 350.C
Conjugate point(s) (in a Riemannian manifold) 364.C
Conjugate point(s) (in the calculus of variations) 46.C
Conjugate pole 350.C
Conjugate Radon transform 218.F
Conjugate representation 362.F
Conjugate series (of a trigonometric series) 159.A
Conjugate space (of a linear topological space) 424.D
Conjugate space (of a normed linear space) 37.D
Conjugate topological 126.B
Conjugation mapping (of a Hopf algebra) 203.E
Conjugation operator 164.K
Conjunction (of propositions) 411.B
Conley, Charles Cameron(1933-1984) 126.E
Conlon, Laurence William(1933-) 154.H
Connected  - (space) 79.C - (space) 79.C
Connected (affine algebraic group) 13.A
Connected (design) 102.K
Connected (graded module) 203.B
Connected (graph) 186.F
Connected (topological space) 79.A
Connected (treatment) 102.B
Connected arcwise (space) 79.B
Connected component 79.A 186.F
Connected component arcwise- 79.B
Connected component strongly 186.F
Connected K- 186.F
Connected Lie subgroup 249.D
Connected locally  - (space) 79.C - (space) 79.C
Connected locally (at a point) 79.B
Connected locally (space) 79.A
Connected locally arcwise (at a point) 79.B
Connected locally arcwise (space) 79. B
Connected locally n- (at a point) 79.C
Connected locally n- (space) 79.C
Connected multiply (plane domain or space) 333.A
Connected n- (pair of topological spaces) 202.L
Connected n- (space) 79.C 202.L
Connected n-ply (plane domain) 333.A
Connected part 150.D
Connected path- (space) 79.B
Connected sequences of functors 200.I
Connected set 79.A
Connected simply (covering Lie group) 249.C
Connected simply (space) 79.C 170
Connected simply, group 13.N
Connected space 79.A
Connected strongly (components) 186.F
Connected sum (of 3-manifolds) 65.E
Connected sum (of oriented compact  -manifolds) 114.F -manifolds) 114.F
Connectedness 79 186.F
Connectedness of real numbers 294.E
Connectedness theorem general, due to W. Fulton and J. Hansen 16.I
Connectedness theorem Zariski 16.X
Connecting homomorphism in cohomology 200.F
Connecting homomorphism in homology 200.C
Connecting homomorphism on homology groups 201.C 201.L
Connecting morphism 200.H 200.I
Connection form 80.E 417.B
Connection formula for the solutions of a differential equation 253.A
Connection of spin and statistics 132.A 150.D
Connection problem 253.A
Connection(s) 80
Connection(s) affine 80.H 286.L
Connection(s) affine, coefficients of 80.L
Connection(s) Cartan 80.M
Connection(s) conformal 80.P
Connection(s) Euclidean 364.B
Connection(s) Euclidean, manifold with 109
Connection(s) flat 80.E
Connection(s) Gauss — Manin (of a variety) 16.V
Connection(s) Levi—Civita 364.B
Connection(s) linear 80.H
Connection(s) locally flat 80.E
Connection(s) metric 80.K
Connection(s) normal 365.C
Connection(s) projective 80.O
Connection(s) Riemannian 80.K 364.B
Connection(s) Riemannian, coefficients of 80.L
Connection(s), canonical affine (on 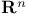 ) 80.J ) 80.J
Connective fiber space, n- 148.D
Connectives, propositional 411.E
Connectivity (of a space) 201.A
Conner, Pierre Euclide, Jr.(1932-) 237.r 431.E 431.r
Connes, Alain(1947-) 136.F 308.H 308.I 308.r 351.L
Conoid, right 111.I
Conoidal neighborhood 274.E
Conormal 323.F
Conormal bundle 274.E
Conormal sphere bundle 274.E
Conservation laws, even-oddness 150.D
Conservative (measurable transformation) 136.C
Conservative chain 260.A
Conservative process 261.B
Conserved axial-vector currents, partially 132.C
Consistency (condition in the multistep method) 303.E
Consistency (of a logical system) 276.D
Consistency (of an estimator) 399.K
Consistency condition 341.I
Consistency of analysis 156.E
Consistency of the axiom of choice and the continuum hypothesis 33.D
Consistency proof 156.D
Consistency proof of pure number theory 156.E
Consistency relative 156.D
Consistency { }- 399.K }- 399.K
Consistent  - 156.E - 156.E
Consistent (finite difference scheme) 304.F
Consistent (formal system) 411.I
Consistent (system of axioms) 35.B
Consistent a.s. 399.K
Consistent and asymptotically normal (CAN) estimator 399.K
Consistent estimator 399.K
Consistent Fisher 399.K
Consistent kernel (in potential theory) 338.E
Consistent test 400.K
Consistent test uniformly 400.K
Consistent { }- 399.K }- 399.K
Consistent-mass scheme 304.D
Constant breadth, curve of 89.C
Constant curvature, space of 364.D App. Table
Constant curvature, surface of 111.I
Constant function 381.C
Constant inclination, curve of 111.F
Constant mapping 381.C
Constant pressure, specific heat at 419.B
Constant sheaf 383.D
Constant sheaf locally constructible 16. A A
Constant stratum,  - 418.E - 418.E
Constant term of a formal power series 376.A
Constant term of a polynomial 337.B
Constant term unfolding 51.D
Constant variational formula 163.E
Constant volume, specific heat at 419.B
Constant width, curve of 111.E
Constant(s) 165.C
Constant(s) arbitrary (in a general solution of a differential equation) 313.A
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -
- 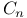 (on Kodaira dimension)
(on Kodaira dimension)  -functions)
-functions)  -
-  -
-  - (space)
- (space) -manifolds)
-manifolds) 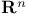 )
)  }-
}-