|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Class 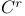 , regular mapping of 208.B , regular mapping of 208.B
Class 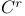 , vector field of 105.M , vector field of 105.M
Class 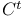 , tensor field of 108.O , tensor field of 108.O
Class 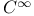 , function of 106.K , function of 106.K
Class 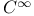 , function of (of many variables) 58.B , function of (of many variables) 58.B
Class 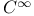 , mapping of 286.E , mapping of 286.E
Class 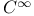 , oriented singular r-simplex of 108.T , oriented singular r-simplex of 108.T
Class 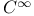 , partition of unity of 108.S , partition of unity of 108.S
Class 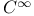 , singular r-chain of 108.T , singular r-chain of 108.T
Class 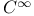 , singular r-cochain of 108.T , singular r-cochain of 108.T
Class 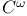 , function of 106.K , function of 106.K
Class  , curve of 364.A , curve of 364.A
Class 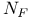 , null set of 169.E , null set of 169.E
Class 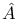 -characteristic (of a real oriented vector Bundle) 237.F -characteristic (of a real oriented vector Bundle) 237.F
Class 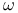 , function of 84.D , function of 84.D
Class 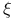 , function of 84.D , function of 84.D
Class (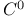 ), semigroup of 378.B ), semigroup of 378.B
Class (in axiomatic set theory) 33.C 381.G
Class (of a lattice group) 13.P
Class (of a nilpotent group) 190.J
Class (of a plane algebraic curve) 9.B
Class (of a quadratic form) 348.H 348.I
Class 0, function of 84.D
Class 1, function of 84.D
Class 1, function of at most 84.D
Class algebra (of central simple algebras) 29.E
Class ambig (of a quadratic field) 347. F
Class Bravais 92.B
Class canonical (of an algebraic curve) 9.C
Class canonical cohomology 59.H
Class canonical divisor 11.D
Class characteristic (of a fiber bundle) 147.K
Class characteristic (of a vector bundle) 56
Class characteristic (of an extension of module) 200.K
Class characteristic (of foliations) 154.G
Class characteristic, of a manifold 56.F
Class characteristic, of codimension q 154.G
Class Chern (of a 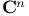 -bundle) 56.C -bundle) 56.C
Class Chern (of a manifold) 56.F
Class Chern (of a real 2n-dimensional almost complex manifold) 147.N
Class Chern (of a U(n)-bundle) 147.N
Class cohomology 200.H
Class combinational Pontryagin 56.H
Class complete 398.B
Class completely additive 270.B
Class conjugacy (of an element of a group) 190.C
Class countably additive 270.B
Class crystal 92.B
Class curve of the second 78.K
Class differential divisor (of a Riemann surface) 11.D
Class divisor (on a Riemann surface) 11.D
Class Dynkin 270.B
Class equivalence 135.B
Class ergodic 260.B
Class essentially complete 398.B
Class Euler — Poincare (of a manifold) 56.F
Class Euler — Poincare (of an oriented 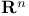 -bundle) 56.B -bundle) 56.B
Class field 59.B
Class field theory 59
Class field theory, local 59.G
Class field tower problem 59.F
Class field, absolute 59.A
Class finitely additive 270.B
Class formation 59.H
Class function (on a compact group) 69.B
Class fundamental (of a Poincare pair) 114.J
Class fundamental (of an Eilenberg — MacLane space) 70.F
Class fundamental (of the Thom complex  ) 114.G ) 114.G
Class fundamental, with coefficient 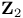 65.B 65.B
Class generalized Hardy 164.G
Class Gevrey 58.G 125.U
Class group divisor 11 .D
Class group of congruence 14.H
Class Hardy 43.F 159.G
Class Hilbert — Schmidt 68.I
Class holosymmetri 92.B
Class homology 200.H 201.B
Class homotopy 202.B
Class ideal (of a Dedekind domain) 67.K
Class ideal (of an algebraic number field) 14.E
Class ideal, in the narrow sense 14.G 343.F
Class idele 6.D
Class idele, group 6.D
Class linear equivalence (of divisors) 16.M
Class main 241.A
Class mapping 202.B
Class minimal complete 398.B
Class monotone 270.B
Class multiplicative 270.B
Class n, function of 84.D
Class n, projective set of 22.D
Class nuclear 68.I
Class number (of a Dedekind domain) 67.K
Class number (of a simple algebra) 27.D
Class number (of an algebraic number field) 14.E
Class of a quadratic form over an algebraic number field 348.H
Class of Abelian groups 202.N
Class oriented cobordism 114.H
Class Pontryagin (of a manifold) 56.F
Class Pontryagin (of an 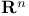 -bundle) 56.D -bundle) 56.D
Class proper 381.G
Class q-dimensional homology 201.B
Class residue (modulo an ideal in a ring) 368.F
Class Steifel — Whitney (of a differentiable manifold) 147.M
Class Stiefel — Whitney (of a manifold) 56.F
Class Stiefel — Whitney (of a topological manifold) 56.F
Class Stiefel — Whitney (of an 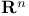 -bundle) 56.B -bundle) 56.B
Class Stiefel — Whitney (of an O(n)-bundle) 147.M
Class surface of the second 350.D
Class the Dynkin, theorem 270.B
Class the monotone, theorem 270.B
Class theorems, complete 398.D
Class Todd 237.F
Class total Chern 56.C
Class total Pontryagin 56.D
Class total Stiefel — Whitney 56.B
Class trace 68.I
Class universal Chern 56.C
Class universal Euler — Poincare 56.B
Class universal Stiefel — Whitney 56.B
Class unoriented cobordism 114.H
Class Wu (of a topological manifold) 56.F
Class Zygmund 159.E
Classical (potential) 402.G
Classical (state) 402.G
Classical compact real simple Lie algebra 248.T
Classical compact simple Lie group 249.L
Classical complex simple Lie algebra 248.S
Classical complex simple Lie group 249.M
Classical descriptive set theory 356.H
Classical dynamical system 126.L 136.G
Classical group(s) 60.A
Classical group(s), infinite 147.I 202.V
Classical logic 411.L
Classical mechanics 271.A
Classical risk theory 214.C
Classical solution (to Plateau’s problem) 275.C
Classical statistical mechanics 402.A
Classical theory of the calculus of variations 46.C
Classification (with respect to an equivalence relation) 135.B
Classification theorem classification theory of Riemann surfaces 367.E
Classification theorem first (in the theory of obstructions) 305.B
Classification theorem Hopf 202.I
Classification theorem on a fiber bundle 147.G
Classification theorem second (in the theory of obstructions) 305.C
Classification theorem third (in the theory of obstructions) 305.C
Classificatory procedure 280.I
Classifying mapping (map) (in the classification theorem of fiber bundles) 147.G
Classifying space (of a topological group) 174.G 174.H
Classifying space for 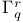 -structures 154.E -structures 154.E
| Classifying space n- (of a topological group) 147.G
Classifying space, cohomology rings of App. A Table
Clatworthy, Willard H. STR
Clausius, Rudolf Julius Emmanuel(1822-1888) 419.A
Clebsch — Gordan coefficient 258.B 353.B
Clebsch, Rudolf Friedrich Alfred(1833-1872) 11.B 226.G 353.B
Clemence, Gerald Maurice(1908-) 55.r 392.r
Clemens, Charles Herbert(1939-) 16.J
Clenshaw — Curtis formulas 299.A
Clenshaw, Charles William(1926-) 299.A
Clifford algebras 61
Clifford group 61.D
Clifford group, reduced 61.D
Clifford group, special 61.D
Clifford number 61.A
Clifford torus 275.F
Clifford torus, generalized 275.F
Clifford, Alfred H.(1908-) 190.r 243.G
Clifford, William Kingdon(1845-1879) 9.C 61.A 61.D 275.F
Clinical trials 40. F
Closable operator 251.D
Closed absolutely (space) 425.U
Closed algebraically (field) 149.I
Closed algebraically (in a field) 149.I
Closed arc 93.B
Closed boundary 164.C
Closed braid 235.F
Closed convex curve 111.E
Closed convex hull 424.H
Closed convex surface 111.I
Closed covering 425.R
Closed curve, simple 93.B
Closed differential 367.H
Closed differential form 105.Q
Closed formula 276.A 299.A
Closed formula in predicate logic 411.J
Closed geodesic 178.G
Closed graph theorem 37.I 251.D 424.X
Closed group 362.J
Closed H- (space) 425.U
Closed half-line (in affine geometry) 7.D
Closed half-space (of an affine space) 7.D
Closed hyperbolic, orbit 126.G
Closed ideals in 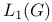 192.M 192.M
Closed image (of a variety) 16.I
Closed integrally (ring) 67.I
Closed interval 140
Closed interval in 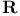 355.C 355.C
Closed k- (algebraic set) 13.A
Closed linear subspace (of a Hilbert space) 197.E
Closed manifold 105.B
Closed mapping 425.G
Closed multiplicatively, subset (of a ring) 67.I
Closed operator (on a Banach space) 251.D
Closed orbit 126.D 126.G
Closed orbit hyperbolic 126.G
Closed path (in a graph) 186.F
Closed path (in a topological space) 170
Closed path direct 186.F
Closed path, space of 202.C
Closed plane domain 333.A
Closed quasi-algebraically (field) 118.F
Closed r- (space) 425. U
Closed range theorem 37.J
Closed real, field 149.N
Closed Riemann surface 367.A
Closed set 425.B
Closed set locally 425.J
Closed set relative 425.J
Closed set Zariski 16.A
Closed set, system of 425.B
Closed subalgebra 36.B
Closed subgroup (of a topological group) 423.D
Closed submanifold (of a 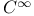 -manifold) 105.L -manifold) 105.L
Closed subsystem (of a root system) 13.L
Closed surface 410.B
Closed surface in a 3-dimensional Euclidean space 111.I
Closed system 419.A
Closed system entropy 402.G
Closed term (of a language) 276.A
Closed Zariski 16.A
Closure 425.B
Closure (in a matroid) 66.G
Closure (of an operator) 251.D
Closure convex (in an affine space) 7.D
Closure finite (cell complex) 70.D
Closure integral (of a ring) 67.I
Closure operator 425.B
Closure Pythagorean (of a field) 155.C
Closure, algebraic (of a field) 149.I
Closure-preserving covering 425.X
Clothoid 93.H
Clough, Ray William, Jr.(1920-) 304.r
Cloverleaf knot 235.C
Cluster 375.F
Cluster decomposition Hamiltonian 375.F
Cluster point 425.O
Cluster set(s) 62.A
Cluster set(s) boundary 62.A
Cluster set(s) curvilinear 62.C
Cluster set(s) interior 62.A
Cluster value 62.A
Cluster value theorem 43.G
Clustering property 402.G
CN App. A Table
Co-echelon space 168.B
Co-NP 71.E
Coalgebra 203.F
Coalgebra cocommutative 203. F
Coalgebra dual 203.F
Coalgebra graded 203.B
Coalgebra homomorphism 203.F
Coalgebra quotient 203.F
Coanalytic set 22.A
Coarse moduli scheme 16.W
Coarse moduli space of curves of genus g 9.J
Coarser relation 135.C
Coarser topology 425.H
Coates, John H.(1945-) 118.D 182.r 450.J 450.r
Cobordant 114.H
Cobordant foliated 154.H
Cobordant h- 114.I
Cobordant mod 2 114.H
Cobordant normally 114.J
Cobordism class 114.H
Cobordism class oriented 114.H
Cobordism class unoriented 114.H
Cobordism group complex 114.H
Cobordism group of homotopy n-spheres, h- 114.I
Cobordism group oriented 114.H
Cobordism group unoriented 114.H
Cobordism ring 114.H
Cobordism ring complex 114.H
Cobordism theorem, h- 114.F
Cobordism, knot 235.G
Coboundary (coboundaries) 200.H
Coboundary (in a cochain complex) 201.H
Coboundary (in the theory of generalized analytic functions) 164.H
Coboundary homomorphism (on cohomology groups) 201.L
Coboundary module of 200.F
Coboundary operator 200.F
Cobounded 201.P
Cochain complex 200.F 201.H
Cochain complex singular 201.H
Cochain equivalence 200.F
Cochain homotopy 200.F
Cochain mapping 200.F 201.H
Cochain subcomplex 200.F
Cochain(s) 200.H 201.H
Cochain(s) (products of) 201.K
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



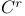 , regular mapping of
, regular mapping of 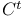 , tensor field of
, tensor field of 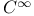 , function of
, function of 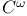 , function of
, function of  , curve of
, curve of 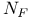 , null set of
, null set of 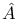 -characteristic (of a real oriented vector Bundle)
-characteristic (of a real oriented vector Bundle) 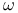 , function of
, function of 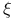 , function of
, function of 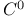 ), semigroup of
), semigroup of 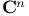 -bundle)
-bundle) 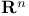 -bundle)
-bundle)  )
) 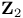
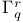 -structures
-structures