|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Additivity countable 270.D
Additivity for the contours (in the curvilinear integral) 94.D
Additivity of probability 342.B
Address 75.B
Address, single-, instructions 75.C
Adele 6.C
Adele and idele 6
Adele group of a linear algebraic group 6.C
Adele group of an algebraic group 13.P
Adele ring (of an algebraic number field) 6.C
Adele, principal 6.C
Adeles and ideles 6
Adem formula App. A Table
Adem relation 64.B
Adem, Jose(1921 -) 64.B 64.C 305.A App.A Table
Adequacy 396.J
Adherent point 425.B
ADI (alternating direction implicit) method 304.F
Adiabatic law 205.B
Adiabatic process, quasistatic 419.B
Adiabatic wall 419.A
Adjacement matrix 186.G
Adjacent (chamber) 13.R
Adjacent (edges) 186.B
Adjacent (germ) 418.E
Adjacent (vertices) 186.B
Adjoin, a set to a field 149.D
Adjoin, a variable to a commutative ring 337.A
Adjoint boundary condition 315.B
Adjoint boundary value problem 315.B
Adjoint differential equations 252.K
Adjoint differential expression 252.K
Adjoint functor 52.K
Adjoint group of a Lie algebra 248.H
Adjoint group of a Lie group 249. P
Adjoint group, isogenous to an algebraic group 13.N
Adjoint Hilbert space 251.E
Adjoint kernel (of a kernel of a potential) 338.B
Adjoint Lie algebra 248.B
Adjoint matrix 269.I
Adjoint operator (of a linear partial differential operator) 322.E
Adjoint operator (of a microdifferential operator) 274.F
Adjoint operator (of a microlocal operator) 274.F
Adjoint operator (on Banach spaces) 37.D 251.D
Adjoint operator (on Hilbert spaces) 251.E
Adjoint representation of a Lie algebra 248.B
Adjoint representation of a Lie group 249.P
Adjoint representation of a linear representation 362.E
Adjoint space (of a linear topological space) 424.D
Adjoint system (of a complete linear system on an algebraic surface) 15.D
Adjoint system of differential equations 252.K
Adjoint, left (linear mapping) 52.K 256.Q
Adjoint, right (linear mapping) 52.K 256.Q
Adjoint, self- see Self-adjoint
Adjunction formula 15.D
Adjustment, sampling inspection with 404.C
Adjustment, seasonal 397.N
Adler — Weisberger sum rule 132.C
Adler, Mark 387.C
Adler, Roy L.(1931-) 126.K 136.E 136.H
Adler, Stephen L.(1939-) 132.C 132.r
Admissible (decision function) 398.B
Admissible (estimator) 399.G
Admissible (extremal length) 143.A
Admissible automorphic representations 450.N
Admissible control 405.A
Admissible function 46.A 304.B
Admissible homomorphism (between  -groups) 190.E -groups) 190.E
Admissible isomorphism (between  -groups) 190.E -groups) 190.E
Admissible lattice (in 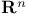 ), S- 182.B ), S- 182.B
Admissible monomial (in Steenrod algebra) 64.B
Admissible normal subgroup 190.E
Admissible ordinal 356.G
Admissible sequence (in Steenrod algebra) 64.B App. Table
Admissible subgroup (of an  -group) 190.E -group) 190.E
Ado theorem 248.F
Ado, Igor Dmitrievich 248.F 248.r
Adriaan, Anthonisz(c.1543-1620) 332
Advanced type (of functional differential equation) 163.A
AF-algebra 36.H
Affect (of an algebraic equation) 172.G
Affectless algebraic equation 172.G
Affine (morphism) 16.D
Affine algebraic group 13.A
Affine algebraic variety 16.A
Affine algebraic variety, quasi- 16.C
Affine arc element 110.C
Affine arc length 110.C
Affine binormal 110.C
Affine connection 80.H 286.L
Affine connection, canonical (on 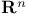 ) 80.J ) 80.J
Affine connection, coefficients of 80.L
Affine coordinates 7.C
Affine curvature 110.C
Affine differential geometry 110.C
Affine frame (of an affine space) 7.C
Affine geometry 7
Affine geometry in the narrower sense 7.E
Affine length 110.C
Affine locally symmetric space 80.J
Affine mapping 7.E
Affine minimal surface 110.C
Affine normal 110.C
Affine principal normal 110.C
Affine ring 16.A
Affine scheme 16.D
Affine space 7.A
Affine symmetric space 80.J
Affine torsion 110.C
Affine transformation(s) 7.E 364.F
Affine transformation(s), group of 7.E
Affine transformation(s), of a manifold with an affine connection 80.J
Affine transformation(s), proper 7.E
Affine transformation(s), regular 7.E
Affine variety 16.A
Affine Weyl group (of a symmetric Riemann space) 413.G
Affinely congruent 7.E
Affinity 7.E
Affinity equivalent 7.E
Age-dependent branching process 44.E
Agmon, Shmuel(1922-) 112.F 112.H 112.Q 323.H 323.r 375.B 375.C
Agnesi, Maria Gaetana(1718-1799) 93.H
Agnesi, witch of 93.H
Aguilar, Joseph 331.F
Ahern, Patrick Robert(1936-) 164.K
Ahlberg, John Harold(1927-) 223.r
Ahlfors finiteness theorem 234.D
Ahlfors five-disk theorem 272.J
Ahlfors function 43.G 77.E
Ahlfors principal theorem 367.B
Ahlfors theory of covering surfaces 367.B
Ahlfors, Lars Valerian(1907-) 17.D 21.N 43.G 43.K 74.r 77.E 77.F.r 122.I 124.B 124.r 143.A 169.E 198.r 234.D 234.E 234.r 272.I 272.J 272.L 352.A 352.B 352.C 352.F 367.B 367.G 367.I 367.r 416 429.D 438.r
Aho, Alfred V 31.r 71.r 75.r 186.r
Aida, Yasuaki(1747-1817) 230
Airy integral App. A Table
Airy, Sir George Biddell(1801-1892) 325.L App.A Table
Aitken interpolation scheme 223.B App. Table
Aitken, Alexander Craig(1895-1967) 223.B App.A Table
Aizawa, Sadakazu(1934-) 286.X
Aizenman, Michael(1945-) 136.G 340.r 402.G
Akahira, Masafumi(1945-) 128.r 399.K 399.O 400.r
Akahori, Takao(1949-) 72.r
Akaike, Hirotugu(1927-) 421.D
Akaza, Tohru(1927-1983) 234.r
Akbar—Zadeh, Hassan(1927-) 152.C
Akcoglu, Mustafa A.(1934-) 136.B
Akemann, Charles A.(1941-) 36.K
Akhiezer, Naum Ilich(1901-1980) 197.r 251.r 336.r 390.r
Akizuki theorem, Krull — 284.F
Akizuki, Yasuo(1902-1984) 8 59.H 284.F 284.G 368.F
| al-Battani, Mohamed ibn Gabis ibn Sinan, Abu Abdallah(858-929) 26 432.C
al-Khwarizmi(Alkwarizmi), Mohammed ibn Musa(c.780-c.850) 26
Alaoglu theorem, Banach- (in a Banach space) 37.E
Alaoglu theorem, Banach- (in a topological linear space) 424.H
Alaoglu, Leonidas(1914-) 37.E 424.H
Albanese variety 16.P
Albanese variety of a compact Kaehler manifold 232.C
Albanese variety strict 16.P
Albanese, Giacomo(1890-1947) 16.P 232.C
Albert, Abraham Adrian(1905-72) 29.F 29.r 149.r 231.r
Albertus Magnus(1193-1280) 372
Alcuin(735-804) 372
Aleksandrov (Alexandroff), Pavel Sergeevich(1896-1982) 22.I 65.r 93.r 99.r 117.A 117.E 117.F 117.r 201.A 201.r 207.C 273.K 425.S—V 425.r 426.* 426.r
Aleksandrov compactification 207.B
Aleksandrov, Aleksandr Danilovich(1912—) 111.r 178.A 255.D 365.H 425.r
Alekseev, Vladimir Mikhailovich(1932-1980) 420.r
Alekseevskii, Dmitril Vladimirovich(1940-) 364.r
Aleph 49.E
Aleph, alpha ( ) 312.D ) 312.D
Aleph, zero (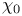 ) 49.E ) 49.E
Alexander cohomology group 201.M
Alexander duality theorem 210.O
Alexander horned sphere 65.G
Alexander ideal (of a knot) 235.C
Alexander matrix (of a knot) 235.C
Alexander polynomial (of a knot) 235.C
Alexander polynomial (of a link) 235.D
Alexander trick 65.D
Alexander — Kolmogorov — Spanier cohomology theory 201.M
Alexander — Whitney mapping (map) 201.J
Alexander, Herbert James(1940-) 344.F
Alexander, James Waddell(1888-1971) 65.G 201.A 201.J 201.M 201.O 201.P 235.A 235.C 235.D 235.E 426
Alexits, Gyoergy(1899-1978) 317.r
Alfsen, Erik Magnus(1930-) 351.L
Alfven wave 259
Alfven, Hannes(1908-) 259.* 259.r
Algebra 8
Algebra  - (of a locally compact Hausdorff group) 36.L - (of a locally compact Hausdorff group) 36.L
Algebra (of sets) 270.B
Algebra (over a field) 203.F
Algebra (semi)simple 29.A
Algebra class (of central simple algebras) 29.E
Algebra class group 29.E
Algebra composition 231.B
Algebra Dirichlet 164.B
Algebra disk 164.B
Algebra division 29.A
Algebra Douglas 164.I
Algebra enveloping 200.L 231.A
Algebra enveloping von Neumann 36.G
Algebra enveloping, universal (of a Lie algebra) 248.J
Algebra extension 29.D 200.L
Algebra exterior (of a linear space) 256.O
Algebra Frobenius 29.H
Algebra full matrix 269.B
Algebra function 164. A
Algebra graded 203.B
Algebra Grassmann (of a linear space) 256.O
Algebra Hecke 29.C 32.D
Algebra homomorphism 29.A
Algebra Hopf 203.H
Algebra Hopf, dual 203.C
Algebra Hopf, elementary 203.D
Algebra Hopf, graded 203.C
Algebra isomorphism 29.A
Algebra j- 384.C
Algebra Jordan 231
Algebra Lie 248.A
Algebra liminal C*- 36.H
Algebra normal j- 384.C
Algebra normal simple 29.E
Algebra of logic 411.A
Algebra operator 308.A
Algebra optional  - 407.B - 407.B
Algebra over a commutative ring 29.A
Algebra PI- 29.J
Algebra quaternion 29.D
Algebra quaternion, generalized 29.D
Algebra quaternion, Hamilton 29.B
Algebra quaternion, totally definite 27.D
Algebra quotient 29.A
Algebra Racah 353.A
Algebra relationship 102.J
Algebra residue class 29.A
Algebra semigroup 29.C
Algebra semigroup, large 29.C
Algebra Staudt 343.C
Algebra Steenrod 64.B
Algebra tensor (on a linear space) 256.K
Algebra Thorn 114.H
Algebra total matrix 269.B
Algebra von Neumann 308.C
Algebra von Neumann, induced 308.C
Algebra von Neumann, reduced 308.C
Algebra zero 29.A
Algebra,  , tail 342.G , tail 342.G
Algebra,  - 270.B - 270.B
Algebra,  -, topological 270.C -, topological 270.C
Algebra,  -, well-measurable 407.B -, well-measurable 407.B
Algebra, AF- 36.H
Algebra, algebraic 29.J
Algebra, alternative 231.A
Algebra, approximately finite 36.H
Algebra, association 102.J
Algebra, associative 29 231.A
Algebra, augmented 200.L
Algebra, AW*- 36.H
Algebra, Azumaya 29.K
Algebra, Banach 36.A
Algebra, Banach *- 36.F
Algebra, boolean 42.A 243.A
Algebra, Boolean, generalized 42.B
Algebra, C*- 36.G
Algebra, C*-, of type I 430.J
Algebra, C*-group (of a locally compact Hausdorff group) 36.L
Algebra, Calkin 36.J 390.I
Algebra, Cayley 54
Algebra, Cayley, general 54
Algebra, central separable 29.K
Algebra, central simple 29.E
Algebra, Clifford 61.A
Algebra, current 132.C
Algebra, cyclic 29.G
Algebra, derived (of a Lie algebra) 248.C
Algebra, distributive 231.A
Algebra, dual 203.F
Algebra, group 29.C 38.L 192.H
Algebra, homological 200.A
Algebra, increasing family of  - 407.B - 407.B
Algebra, linear 8
Algebra, logmodular 164.B
Algebra, multiplier 36.K
Algebra, nonassociative 231.A
Algebra, postliminal C*- 36.H
Algebra, power associative 231.A
Algebra, predictable  - 407.B - 407.B
Algebra, quasi-Frobenius 29.H
Algebra, reduced 23 LB
Algebra, separable 29.F 29.K 200.L
Algebra, simple 29.A
Algebra, solvable 231. A
Algebra, supplemented 200.L
Algebra, symmetric 29.H
Algebra, uniform 164.A
Algebra, uniserial 29.I
Algebra, uniserial, absolutely 29.I
Algebra, uniserial, generalized 29.I
Algebra, unitary 29.A
Algebra, universal enveloping (of a Lie algebra) 248.J
Algebra, vector App. A Table
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -groups)
-groups)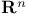 ), S-
), S-  )
) 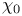 )
)  - (of a locally compact Hausdorff group)
- (of a locally compact Hausdorff group)  -
-