|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics |
|
|
 |
| Предметный указатель |
Casimir 248.J
Casimir element (of a Lie algebra) 248.J
Casorati determinant 104.D
Casorati — Weierstrass theorem (on essential singularities) 198.D
Casorati, Felice(1835-90) 104.D 198.D
Cassandro, M. 402.G
Casselman, William Allen(1941-) 450.r
Cassels, John William Scott(1922-) 14.r 59.r 118.r 182.r 257.r
Cassini oval 93.H
Cassini, Jean Dominique(1625-1712) 93.H
Casson handle 114.M
Casson, Andrew J. 114.K
Cassou—Nogues, Pierrette(1945-) 450.J
Castaing, Charles(1932-) 443.A
Castelnuovo criterion 15.E
Castelnuovo lemma 3.E 9.H
Castelnuovo, Guido(1865-1952) 3.E 9.H 9.r 12.B 12.r 15.B 15.E 15.G 15.H
Castillon, Giovanni Francesco Mauro Melchior Salveminide(1708-1791) 179.A
Casus irreducibilis 10.D App. Table
Catalan constant App. A Table
Catalan, Eugene Charles(1814-1894) App.A Table
Catastrophe point 51.F
Catastrophe set 51.F
Catastrophe theory 51
Catastrophe, elementary 51.E
Categorical (data) 397.B
Categorical (set of closed formulas) 276.F
Categorical system (of axioms) 35.B
Categoricity in powers 276.F
Categories and functors 52
Category 52.A
Category exact 237.J
Category Grothendieck 200.I
Category homotopy of topological spaces 52.B
Category of Abelian groups 52.B
Category of analytic manifolds 52.B
Category of commutative rings 52.B
Category of differentiable manifolds 52.B
Category of groups 52.B
Category of left (right) R-modules 52.B
Category of linear spaces over R 52.B
Category of pointed topological spaces 202.B
Category of rings 52.B
Category of S-objects 52.G
Category of sets 52.B
Category of topological spaces 52.B
Category PL 65.A
Category product 52.A
Category quotient 52.N
Category set of the first 425.N
Category set of the second 425.N
Category shape 382.A
Category, abelian 52.N
Category, additive 52.N
Category, cohomology theory on the 261.Q
Category, diagram in the 52.C
Category, dual 52.F
Catenary 93.H
Catenoid 111.I
Cauchy condensation test 379.B
Cauchy condition (on D-integral and D(*)-integral) 100.E
Cauchy criterion (on the convergence of a sequence of real numbers) 87.C App. Table
Cauchy data 321.A
Cauchy distribution 341.D App. Table
Cauchy existence theorem (for partial differential equations) 320.B
Cauchy filter (on a uniform space) 436.G
Cauchy inequality 211.C App. Table
Cauchy integral formula 198.B
Cauchy integral representation 21.C
Cauchy integral test (for convergence) 379.B
Cauchy integral theorem 198.A
Cauchy integral theorem, stronger form of 198.B
Cauchy net (in a uniform space) 436.G
Cauchy polygon 316.C
Cauchy principal value of an improper integral 216.D
Cauchy principal value of the integral on infinite intervals 216.E
Cauchy problem (for partial differential equations) 315.A 320.B 321.A 325.B
Cauchy problem (of ordinary differential equations) 316.A
Cauchy problem abstract 286.X
Cauchy process 5.F
Cauchy process, asymmetric 5.F
Cauchy process, symmetric 5.F
Cauchy product (of two series) 379.F
Cauchy remainder App.A Table
Cauchy sequence (in a metric space) 273.J
Cauchy sequence (in a uniform space) 436.G
Cauchy sequence (in an 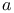 -adic topology) 284.B -adic topology) 284.B
Cauchy sequence (of rational numbers) 294.E
Cauchy sequence (of real numbers) 355.B
Cauchy sum (of a series) 379.A
Cauchy theorem 379.F
Cauchy transform 164.J
Cauchy — Hadamard formula 339.A
Cauchy — Kovalevskaya existence theorem 321.A
Cauchy — Kovalevskaya theorem, abstract 286.Z
Cauchy — Riemann (differential) equation 198.A 274.G
Cauchy — Riemann equation (for a holomorphic function of several complex variables) 21.C
Cauchy — Riemann equation (for a holomorphic function of two complex variables) 320.F
Cauchy — Riemann structure 344.A
Cauchy — Schwarz inequality 211.C App. Table
Cauchy, A.L. 53
Cauchy, Augustin Louis(1789-1857) 4.D 5.F 20 21.C 53 87.C 100.E 107.A 107.B 164.J 165.A 165.r 190.Q 198.A 198.B 198.E 198.F 198.Q 211.C 216.D 216.E 267 273.J 274.G 284.B 286.X 286.Z 294.E 296 301.G 316.A 316.C 316.G 320.B 320.D 320.I 321.A 321.B 339.A 341.D 344.A 379.A 379.B 379.F 379.K 388.B 436.G App.A Tables 9 10.II
Cauer, D.(1889-1918) 179.B
Cauer, Wilhelm(1900-1945) 282.r
Causality, macroscopic 386.C
Cause, most probable 401.E
Caustic 325.L
Cavalieri,(Francesco) Bonaventura(1598-1647) 20 265
Cayley algebras 54
Cayley algebras, general 54
Cayley number 54
Cayley projective plane 54
Cayley theorem (in group theory) 151.H
Cayley theorem, Hamilton — 269.F
Cayley transform (of a closed symmetric operator in a Hilbert space) 251.I
Cayley transformation 269.J
Cayley, Arthur(1821-95) 12.B 54 105.A 137 151.H 157.A 190.Q 226.G 251.I 267 269.F 269.J 285.A
Cazenave, Thierry 286.Y
CCP (chance-constrained programming) 408.B
CCR 377.A
CCR algebra 36.H
CE mapping 382.D
Cebysev see Chebyshev
Cech cohomology group (for topological spaces) 201.L 201.P
Cech cohomology group relative 201.M
Cech cohomology group with coefficient sheaf 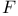 383.F 383.F
Cech compactification, Stone — 207.C
Cech complete space 425.T 436.I
Cech homology group (for topological spaces) 201.M
Cech homology group, relative 201.M
Cech, Edouard(1893-1960) 110.B 110.r 117.E 201.A 201.M 201.P 207.C 383.F 425.T 425.r 426 436.I
Ceder, Jack G(1933-) 425.Y
Ceiling function 136.D
Ceiling states 402.G
Celestial mechanics 55
cell 70.D
Cell (n — q)-dual 65.B
Cell complex 70.D
Cell complex closure finite 70.D
Cell complex countable 70.D
Cell complex Euclidean 70.B
Cell complex finite 70.D
Cell complex locally countable 70.D
Cell complex locally finite 70.D
Cell complex regular 70.D
Cell convex (in an affine space) 7.D
Cell fundamental (of a symmetric Riemann space) 413.F
Cell n- (in a Hausdorff space) 70.D
Cell topological n- 140
Cell unit 140
| Cell-like(CE) 382.D
Cellular approximation theorem 70.D
Cellular cohomology group 201.H
Cellular decomposition (of a Hausdorff space) 70.D
Cellular homology group 201.F 201.G
Cellular mapping (between cell complexes) 70.D
Center (of a central symmetry) 139.B
Center (of a continuous geometry) 85.A
Center (of a group) 190.C
Center (of a hyperbola or ellipse) 78.C
Center (of a lattice) 243.E
Center (of a Lie algebra) 248.C
Center (of a nonassociative algebra) 231.A
Center (of a pencil of hyperplanes) 343.B
Center (of a quadric hypersurface) 7.G
Center (of a quadric surface) 350.A
Center (of a regular polygon) 357.A
Center (of a regular polyhedron) 357.B
Center (of a ring) 368.F
Center (of a solid sphere) 140
Center (of a sphere) 139.I
Center (of a von Neumann algebra) 308.C
Center (of gravity) 271.E
Center (of mass) 271.E
Center manifold theorem 286.V
Center of curvature 111.E
Center of projection 343.B
Center surface 111.I
Centered process 5.B
Centering 5.B
Central composite design 102.M
Central configuration 420.B
Central conic(s) 78.C
Central difference 223.C 304.E App. Table
Central element (in a lattice) 243.E
Central extension (of a group) 190.N
Central figure 420.B
Central limit theorem 250.B
Central moment 397.C
Central motion 126.E
Central potential 315.E
Central processor 75.B
Central quadric hypersurface 7.F 350.G
Central quadric surface 350.B
Central series ascending (of a Lie algebra) 248.C
Central series descending (of a Lie algebra) 248.C
Central series lower (of a group) 190.J
Central series upper (of a group) 190.J
Central simple algebra 29.E
Central simple algebra, similar 29.E
Central symmetry (of an affine space) 139.B
Centralizer (of a subset of a group) 190.C
Centralizer (of a subset of a ring) 368.F
Centrifugal force 271.D
Cerf, Jean(1928-) 114.I
Certainly, almost 342.B 342.D
Certainty equivalent 408.B
Cesari, Lamberto(1910-) 246.r 290.r 314.D 314.r 394.r
Cesaro method of summation of order  379.M 379.M
Cesaro method of summation of order  , summable by 379.M , summable by 379.M
Cesaro, Ernesto(1859-1906) 297.D 379.K 379.M
Ceva theorem 7.A
Ceva, Giovanni(1647?-1734?) 7.A
CFL condition 304.F
CG method 302.D
Chaber, Jozef 273.K
Chacon, Rafael Van Severen(1931-) 136.B 136.H 162
Chadan, Khosrow(1930-) 375.r
Chaikin, S.E. see Khalkin S.E.
Chain 200.H
Chain ascending (in an ordered set) 311.C
Chain ascending (of normal subgroups of a group) 190.F
Chain complex(es) 200.C 200.H 201.B
Chain complex(es) augmented 200.C
Chain complex(es) double 200.E
Chain complex(es) in an Abelian category 201.B
Chain complex(es) of A-modules 200.C
Chain complex(es) oriented simplicial 201.C
Chain complex(es) positive 200.H
Chain complex(es) product double 200.E
Chain complex(es) quotient 200.C
Chain complex(es) relative 200.C
Chain complex(es) singular (of a topological space) 201.E
Chain condition (in an ordered set) 311.C
Chain condition ascending (in an ordered set) 311.C
Chain condition descending (in an ordered set) 311.C
Chain conservative 260.A
Chain descending (in a lattice) 243.F
Chain descending (in an ordered set) 311.C
Chain descending (of (normal) subgroups of a group) 190.F
Chain equivalence 200.C 200.H
Chain general Markov 260.J
Chain homotopy 200.C 200.H
Chain irreducible (a Markov chain) 260.B
Chain mapping 200.C 201.B
Chain mapping over an A-homomorphism 200.C
Chain Markov 260.A
Chain minimal 260.F
Chain normal (in a group) 190.G
Chain normal (in Markov chains) 260.D
Chain q- (of a chain complex) 201.B
Chain recurrent 126.E
Chain recurrent set 126.E 260.B
Chain regular (of integral elements) 428.E
Chain rule 106.C
Chain subcomplex 200.C
Chain theorem 14.J
Chain transformation (between complexes) 200.H
Chain u- 260.I
Chained metric space, well- 79.D
Chaitin complexity, Kolmogorov — 354.D
Chaitin, Gregory J. 71.r 354.D
Chakravarti, Indra-Mohan(1928-) 102.I
Chamber complex 13.R
Chamber positive Weyl 248.R
Chamber Weyl 13.J 248.R
Chance constraint 408.A
Chance move 173.B
Chance-constrained programming 408.A
Chandler, Colston 274.D 274.I 386.C
Chandrasekhar, S. 433.r
Chandrasekharan, Komaravolu(1920-) 121.r 123.r 160.r 379.r 450.r
Chang Chen-Chung(1927-) 276.r 293.r
Chang Sun-Yang(1948-) 164.I
Chang, J.J. 346.E 346.r
Change of variables (in integral calculus) 216.C
Change scalar (of a B-module) 277.L
Change time 261.F 406.B
Channel 375.F
Channel almost finite memory 213.F
Channel coding theory 213.A
Channel d-continuous 213.F
Channel discrete memoryless 213.F
Channel finite memory 213.F
Channel Hilbert space 375.F
Channel noisy 213.A
Channel test 213.E
Channel wave operators 375.F
Chaos 126.N 303.G 433.B
Chaos, propagation of 340.F
Chaplygin, Sergei Alekseevich(1869-1942) 326.B
Chaplygin’s differential equation 326.B
Chapman complement theorem 382.B
Chapman theorem (on 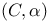 -summation) 379.M -summation) 379.M
Chapman — Kolmogorov equality 261.A
Chapman — Kolmogorov equation 260.A
Chapman — Robbins — Kiefer inequality 399.D
Chapman, D.G.(1920-) 399.D
Chapman, Sydney(1888-1970) 41.E 260.A 261.A 379.M 402.H 402.r
Chapman, Thomas A.(1940-) 65.C 382.B 382.D
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



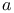 -adic topology)
-adic topology) 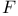

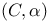 -summation)
-summation)