|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
Spherical (space form) 412.H
Spherical astronomy 392
Spherical Bessel function 39.B
Spherical coordinates 90.C App. Table
Spherical derivative (for an analytic or meromorphic function) 435.E
Spherical excess 432.B
Spherical Fourier transform 437.Z
Spherical function (on a homogeneous space) 437.X
Spherical function Laplace 393.A
Spherical function zonal (on a homogeneous space) 437.Y
Spherical function(s) 393
Spherical G-fiber homotopy type 431.F
Spherical geometry 285.D
Spherical harmonic function 193.C
Spherical harmonics, biaxial 393.D
Spherical indicatrix (of a space curve) 111.F
Spherical modification 114.F
Spherical representation of a differentiable manifold 111.G
Spherical representation of a space curve 111.F
Spherical representation of a unimodular locally compact group 437.Z
Spherical space 285.D
Spherical triangle 432.B App. Table
Spherical trigonometry 432.B
Spherical type 13.R
Spherical wave 446
Spheroidal coordinates 133.D App. Table
Spheroidal wave function 133.E
Spin 132.A 258.A 415.G
Spin and statistics, connection of 132.A 150.D
Spin ball 351.L
Spin bundle 237.F
Spin continuous 258.A
Spin mapping (map) 237.G
Spin matrix, Pauli 258.A 415.G
Spin representation (of SO(n)) 60.J
Spin representation (of Spin(n, C)) 61.E
Spin representation even half- 61.E
Spin representation half- 61.E
Spin representation odd half- 61.E
Spin systems, lattice 402.G
Spin-flip model 340.C
Spin-structure 237.F 431.D
Spinc bundle 237.F
Spindler, Heinz 16.r
Spinor contravariant 258.A
Spinor covariant 258.A
Spinor dotted 258.B
Spinor even half- 61.E
Spinor group 60.I61.D
Spinor group complex 61.E
Spinor mixed, of rank (k, n) 258.A
Spinor odd half- 61.E
Spinor representation (of rank k) 258.A
Spinor undotted 258.B
Spinor(s) 61.E
Spinorial norm 61.D
Spiral 93.H
Spiral Archimedes 93.H
Spiral Bernoulli 93.H
Spiral Cornu 93.H
Spiral equiangular 93.H
Spiral hyperbolic 93.H
Spiral logarithmic 93.H
Spiral reciprocal 93.H
Spitzer, Frank Ludwig 44.C 250.r 260.E J
Spivak normal fiber space 114.J
Spivak, Michael D. 114.J 191.r 365.r
SPLINE 223.F
Spline interpolation 223.F
Spline natural 223.F
Split ((B,N)-pair) 151.J
Split (cocycle in an extension) 257.E
Split (exact sequence) 277.K
Split extension (of a group) 190.N
Split k- (algebraic group) 13.N
Split K- (algebraic torus) 13.D
Split k-quasi-(algebraic group) 13.O
Split maximal k, torus 13.Q
Split torus, maximal k- 13.Q
Splitting field for an algebra 362.F
Splitting field for an algebraic torus 13.D
Splitting field minimal (of a polynomial) 149.G
Splitting field of a polynomial 149.G
Splitting ring 29.K
Splitting, Heegaard 65.C
Spot prime 439.H
Sprindzhuk, Vladimir Gennadievich 118.D 430.C
Springer, George 367.r
Springer, Tonny Albert 13.A I O P r
Spur 269.F
Square integrable 168.B
Square integrable unitary representation 437.M
Square latin 241
Square least, approximation 336.D
Square matrix 269.A
Square matrix of the sum of, between classes 280.B
Square matrix of the sum of, within classes 280.B
Square method of least 303.I
Square middle-, method 354.B
Square net 304.E
Square numbers 4.D
Square Room 241.D
Square Shrikhande 102.K
Square Youden 102.K
Square Youden, design 102.K
Square(s) Euler 241.B
Square-free integer 347.H
Srinivasan, B. App. B Table
Srinivasan, T.P. 164.G
Srivastava, Muni Shanker 280.r
Stability 286.S 303.E 394
Stability 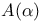 - 303.G - 303.G
Stability 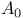 - 303.G - 303.G
Stability A- 303.G
Stability absolute 303.G
Stability conjecture 126J
Stability exchange of 286.T
Stability group 362.B
Stability interval of absolute 303.G
Stability interval of relative 303.G
Stability orbital (of a solution of a differential equation) 394.D
Stability principle oflinearized 286.S
Stability region of absolute (of the Runge-Kutta (P, p) method) 303.G
Stability region of relative 303.G
Stability relative 303.G
Stability stiff- 303.G
Stability structural 290.A
Stability structural, theorem 126.J
Stability subgroup (of a topological group) 431.A
Stability theorem  - 126.J - 126.J
Stability theorem structural 126.J
Stabilizer (in a permutation group) 151.H
Stabilizer (in a topological transformation group) 431.A
Stabilizer (in an operation of a group) 362.B
Stabilizer reductive 199.A
Stable 394.A
Stable  -structurally 126.H -structurally 126.H
Stable  126.H 126.H
Stable (coherent sheaf on a projective variety) 241.Y
Stable (compact leaf) 154.D
Stable (discretization, initial value problems) 304.D
Stable (equilibrium solution) 286.S
Stable (initial value problem) 304.F
Stable (invariant set) 126.F
Stable (linear function) 163.H
Stable (manifold) 126.G
Stable (minimal submanifold) 275.B
Stable (static model in catastrophe theory) 51.E
Stable absolutely 303.G
Stable asymptotically 126.F 286.S 394.B
| Stable cohomology operation 64.B
Stable conditionally 394.D
Stable curve 9.K
Stable distribution 341.G
Stable distribution (of Thom spectrum) 114.G
Stable distribution of classical groups 202.V
Stable distribution of k-stem 202.U
Stable distribution quasi- 341.G
Stable distribution semi- 341.G
Stable distribution stable homotopy group 202.T App. Table
Stable exponentially 163.G 394.B
Stable externally, set 186.I
Stable globally asymptotically 126.F
Stable in both directions (Lyapunov stable) 394.A
Stable internally, set 186.I
Stable Lagrange 126.E
Stable Lyapunov 126.F
Stable Lyapunov, in the positive or negative direction 394.A
Stable manifold 126.G J
Stable negatively Lagrange 126.E
Stable negatively Poisson 126.E
Stable one-side, for exponent  App. A Table App. A Table
Stable orbitally 126.F
Stable point 16.W
Stable Poisson 126.E
Stable positively Lagrange 126.E
Stable positively Poisson 126.E
Stable primary cohomology operation 64.C
Stable process 5.F
Stable process exponent of 5.F
Stable process one-sided, of the exponent a 5.F
Stable process strictly 5.F
Stable process symmetric 5.F
Stable range (of embeddings) 114.D
Stable reduction (of a curve) 9.K
Stable reduction (of an Abelian variety) 3.N
Stable reduction potential (of an Abelian variety) 3.N
Stable reduction theorem 3.N 9.K
Stable relatively 303.G
Stable secondary cohomology operation 64.C
Stable set 173.D
Stable set externally 186.I
Stable set internally 186.I
Stable solution (of the Hill equation) 268.E
Stable state 260.F 394.A 404.A
Stable uniformly 394.B
Stable uniformly asymptotically 163.G 394.B
Stable uniformly Lyapunov 126.F
Stable vector bundle (algebraic) 16.Y
Stable vector bundle (topological) 237.B
Stably almost complex manifold 114.H
Stably equivalent (vector bundles) 237.B
Stably fiber homotopy equivalent 237.I
Stably parallelizable (manifold) 114.I
STACK 96.E
Stage method, (P+ 1)- 303.D
Stalk (of a sheaf over a point) 16.AA 383.B
Stallings, John Robert, Jr. 65.A C E F
Stampacchia, Guido 440.r
Stanasila, Octavian 23.r
Stancu-Minasian, I.M. 408.r
Standard (in nonstandard analysis) 293.B
Standard (transition probability) 260.F
Standard Borel space 270.C
Standard complex (of a Lie algebra) 200.O
Standard defining function 125.Z
Standard deviation (characteristics of the distribution) 397.C
Standard deviation (of a probability distribution) 341.B
Standard deviation (of a random variable) 342.C
Standard deviation population 396.C
Standard deviation sample 396.C
Standard form 241.A
Standard form (of a difference equation) 104.C
Standard form Legendre — Jacobi (of an elliptic integral) 134.A App.A Table
Standard form of the equation (of a conic section) 78.C
Standard Gaussian distribution 176.A
Standard Kahler metric (of a complex projective space) 232.D
Standard measurable space 270.D
Standard normal distribution 341.D
Standard parabolic/c-subgroup 13.Q
Standard part (in nonstandard analysis) 293.D
Standard q-simpiex 201.E
Standard random walk 260.A
Standard resolution (of Z) 200.M
Standard sequence 400.K
Standard set 22.I
Standard vector space (in a complex) 13.R
Standard vector space (in a Euclidean complex) 70.B
Standard vector space (in a projective space) 343.B
Standard vector space (in a simplicial complex) 70.C
Standard vector space (of a subset defined by a covering) 425.R
Standard vector space (of an affine space) 7.A
Standard vector space open 70.B C
Stanley, Harry Eugene 402.r
Stanley, Richard Peter 16.Z
Stapp, Henry Pierce 146.C 274.D I
Star body, bounded 182.C
Star convergence 87.K
Star convergence (o)- 87.L
Star convergence relative uniform 310.F
Star refinement (of a covering) 425.R
Star region 339.D
Star topology, weak (of a normed linear space) 37.E 424.H
Star-finite (covering of a set) 425.R
Star-finite property 425.S
Stark, Harold Mead 83.r 118.D 182.G 347.E 450.E
Starmer inequality, Powers- 212.B
Start node 281.D
Starting values (in a multistep method) 303.E
Stasheff, James Dillon 56.r 201.r
State (in Ising model) 340.B
State (in quantum mechanics) 351.B
State bound 351.D
State ceiling 402.G
State completeness of the scattering 150.D
State equation of 419.A
State equilibrium 136.H 340.B 419.A
State estimator 86.E
State even 415.H
State fictitious 260.F
State final 31.B
State Gibbs 340.B
State ground 402.G
State in- 150.D 386.A
State initial 31.B
State instantaneous 260.F 261.B
State internal 31.B
State odd 415.H
State of statistical control 404.A
State out- 150.D 386.A
State scattering 395.B
State space 126.B
State space (in catastrophe theory) 51.B
State space (of a dynamical system) 126.B
State space (of a Markov process) 261.B
State space (of a stochastic process) 407.B
State stable 260.F 394.A 404.A
State stationary 340.C 351.D
State sum over 402.D
State unstable 394.A
State variable 127.A
State(s) (of a C*-algebra) 308.D
State-space approach 86.A
static 51.B
Static model (in catastrophe theory) 51.B
Stationary capacity 213.F
Stationary curve (of a variation problem) 46.B
Stationary curve (of the Euler — Lagrange differential equation) 324.E
Stationary function 46.B
Stationary iterative process, linear 302.C
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



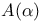 -
- 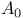 -
-  -
-  -structurally
-structurally 
