|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
Space path (of a Markov process) 261.B
Space path-connected 79.B
Space pathological 65.F
Space Peirce 231.B
Space perfectly normal 425.Q
Space perfectly separable 425.P
Space phase 126.B 163.C 402.C
Space physical Hilbert 150.G
Space pinching a set to a point 202.E
Space polar 191.I
Space Polish 22.I 273.J
Space pre-Hilbert 197.B
Space precompact metric 273.B
Space precompact uniform 436.H
Space principal (of a flag) 139.B
Space principal half- 139.B
Space probability 342.B
Space product 425.K
Space product measure 270.H
Space product metric 273.B
Space product topological 425.K
Space product uniform 436.E
Space projective limit 210.C
Space projective, over  147.E 147.E
Space projectively flat App. A Table
Space pseudocompact 425.S
Space pseudometric 273.B
Space pseudometrizable uniform 436.F
Space Q- 425.BB
Space quasi-Banach 37.O
Space quasicompact 408.S
Space quasidual (of a locally compact group) 437.I
Space quasinormed linear 37.0
Space quaternion hyperbolic 412.G
Space quotient 425.L
Space quotient (by a discrete transformation group) 122.A
Space quotient (by a transformation group) 122.A
Space quotient (of a linear space with respect to an equivalence relation) 256.F
Space quotient topological 425.L
Space r-closed 425.U
Space ramified covering 23.B
Space real Hilbert 197.B
Space real hyperbolic 412.G
Space real interpolation 224.C
Space real linear 256.A
Space real projective 343.D
Space real-compact 425.BB
Space reduced product 202.Q
Space reflection 359.B
Space reflexive Banach 37.G
Space regular 425.Q
Space regular Banach 37.G
Space representation (for a Banach algebra) 36.D
Space representation (of a representation of a Lie algebra) 248.B
Space representation (of a representation of a Lie group) 249.O
Space representation (of a unitary representation) 437.A
Space Riemannian 364.A
Space Riesz 310.B
Space right coset (of a topological group) 423.E
Space right projective 343.H
Space right quotient (of a topological group) 423.E
Space ringed 383.H
Space sample 342.B 396.B 398.A
Space scale of Banach 286.Z
Space Schwartz 424.S
Space separable 425.P
Space separable metric 273.E
Space separated 425.Q
Space separated uniform 436.C
Space sequential 425.CC
Space sequentially compact 425.S
Space sheaf 383.C
Space shrinking, to a point 202.E
Space Siegel upper half-, of degree n 32.F
Space Siegel, of degree n 32.F
Space simply connected 79.C 170
Space smashing, to a point 202.E
Space Sobolev 168.B
Space Spanier cohomology theory, Alexander — Kolmogorov- 201.M
Space spherical 285.D
Space Spivak normal fiber 114.J
Space standard Borel 270.C
Space standard measurable 270.C
Space standard vector (of an affine space) 7.A
Space state (in static model in catastrophe theory) 51.B
Space state (of a dynamical system) 126.B
Space state (of a Markov process) 261 B
Space state (of a stochastic proccess) 407.B
Space Stein 23.F
Space stratifiable 425.Y
Space strongly paracompact 425.S
Space structure (of a Banach algebra) 36.D
Space subbase for 425.F
Space Suslin 22.I 425.CC
Space symmetric Hermitian 412.E
Space symmetric homogeneous 412.B
Space symmetric Riemannian 412
Space symmetric Riemannian homogeneous 412.B
Space tangent 105.H
Space tangent vector 105.H
Space Teichmiiller 416
Space tensor, of degree k 256.J
Space tensor, of type (p, q) 256.J
Space test function 125.S
Space Thorn 114.G
Space Tikhonov 425.Q
Space time parameter 260.A
Space topological complete 436.I
Space topological linear 424.A
Space topological vector 424.A
Space total (of a fiber bundle) 147.B
Space total (of a fiber space) 148.B
Space totally bounded metric 273.B
Space totally bounded uniform 436.H
Space totally disconnected 79.D
Space transformation (of an algebraic group) 13.G
Space underlying topological (of a complex manifold) 72.A
Space underlying topological (of a topological group) 423.A
Space uniform topological 436.C
Space uniformizable topological 436.H
Space uniformly locally compact 425.V
Space unisolvent 142.B
Space universal covering 91.B
Space universal Teichmueller 416
Space vector, over K 256.A
Space velocity phase 126.L
Space weakly symmetric Riemannian 412.J
Space well-chained metric 79.D
Space wild 65.F
Space(s) 381.B
Space-time Brownian motion 45.F
Space-time inversion 258.A
Space-time manifold 359.D
Space-time, Minkowski 359.B
Spacelike 258.A 359.B
Span (a linear subspace by a set) 256.F
Span (of a domain) 77.E
Span (of a Riemann surface) 367.G
Spanier, Edwin Henry 64.r 70.r 148.r 170.r 201.M.r 202.I r305.r
Spanning tree 186.G
sparse 302.C
Spath type division theorem (for microdifferential operators) 274.F
Spath, R. A. 274.F314.A
Spatial (*-isomorphism on von Neumann algebras) 308.C
Spatial tensor product 36.H
Spatially homogeneous (process) 261.A
Spatially isomorphic (automorphisms on a measure space) 136.E
Spearman rank correlation 371.K
Spearman, Charles 346.F r
Spec (spectrum) 16.D
| Specht, Wilhelm 110.r 151.r 190.r
Special Clifford group 61.D
Special divisor 9.C
Special flow 136.D
Special function of confluent type 389.A
Special function of ellipsoidal type 389.A
Special function of hypergeometric type 389.A
Special function(s) 389 App. Table
Special functional equations 388
Special isoperimetric problem 228.A
Special Jordan algebra 231.A
Special linear group 60.B
Special linear group (over a noncommutative field) 60.O
Special linear group of degree n over K 60.B
Special linear group projective 60.B
Special linear group projective (over a noncommutative field) 60.O
Special orthogonal group 60.I
Special orthogonal group complex 60.I
Special orthogonal group over Kwith respect to 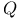 60.K 60.K
Special principle of relativity 359.B
Special relativity 359.B
Special representation (of a Jordan algebra) 231.C
Special surface 110.A
Special theory of perturbations 420.E
Special theory of relativity 359.A
Special unitary group 60.F
Special unitary group (relative to an  -Hermitian form) 60.O -Hermitian form) 60.O
Special unitary group over K 60.H
Special unitary group projective, over K 60.H
Special universal enveloping algebra (of a Jordan algebra) 231.C
Special valuation 439.B
Speciality index  - (of a divisor of an algebraic curve) 9.F - (of a divisor of an algebraic curve) 9.F
Speciality index (of a divisor of an algebraic curve) 9.C
Speciality index (of a divisor on an algebraic surface) 15.D
Specialization 16.A
Specialization (in etale topology) 16.AA
Species ellipsoidal harmonics of the first, second, third or fourth 133.C
Species Lame functions of the first, second, third or fourth 133.C
Species singular projective transformation of the hth 343.D
Species singular quadric hypersurface of the hth (in a projective space) 343.E
Specific heat at constant pressure 419.B
Specific heat at constant volume 419.B
Specific resistance 130.B
Specification 401.A
Specification problem of 397.P
Specificity 346.F
Specker, W.H. 142.C
Spector, Clifford 81.r 156.E r r
Spectral analysis 390.A
Spectral concentration 331.F
Spectral decomposition 126.J 395.B
Spectral density, quadrature 397.N
Spectral functor 200.J
Spectral geometry 391.A
Spectral integral 390.D
Spectral invariant 136.E
Spectral mapping theorem 251.G
Spectral measure 390.B K C
Spectral measure complex 390.D
Spectral measure maximum 390.G
Spectral measure real 390.D
Spectral method 304.B
Spectral operator 390.K
Spectral property 136.E
Spectral radius 126.K 251.F 390.A
Spectral representation 390.E
Spectral representation complex 390.E
Spectral resolution 390.E
Spectral resolution complex 390.E
Spectral sequence 200.J
Spectral sequence (of a fiber space) 148.E
Spectral sequence cohomology 200.J
Spectral sequence Hodge 16.U
Spectral synthesis 36.L
Spectral theorem 390.E
Spectrally isomorphic (automorphisms on a measure space) 136.E
Spectrum 390.A
Spectrum (in homotopy theory) 202.T
Spectrum (of a commutative ring) 16.D
Spectrum (of a domain in a Riemannian manifold) 391.A
Spectrum (of a hyperfunction) 274.E
Spectrum (of a linear operator) 251.F 390.A
Spectrum (of a spectral measure) 390.C
Spectrum (of an element of a Banach algebra) 36.C
Spectrum (of an integral equation) 217.J
Spectrum absolutely continuous 390.E
Spectrum condition 150.D
Spectrum continuous (of a linear operator) 390.A
Spectrum continuous (of an integral equation) 217.J
Spectrum countable Lebesgue 136.E
Spectrum discrete 136.E 390.E
Spectrum Eilenberg — MacLane 202.T
Spectrum essential 390.E I
Spectrum formal (of a Noetherian ring) 16.X
Spectrum forp-forms 391.B
Spectrum intermittent 433.C
Spectrum joint 36.M
Spectrum Kolmogorov 433.C
Spectrum point 390.A
Spectrum pure point 136.E
Spectrum quasidiscrete 136.E
Spectrum residual 390.A
Spectrum simple 390.G
Spectrum singular 125.CC 345.A 390.A
Spectrum singular (of a hyperfunction) 274.E
Spectrum singularity (of a hyperfunction) 125.CC 274.E
Spectrum sphere 202.T
Spectrum stable homotopy group of the Thorn 114.G
Spectrum Thorn 114.G 202.T
Speed measure 115.B
Speer, Eugene Richard 146.A
Speiser theorem, Hilbert- 172.J
Speiser, Andreas 151.r 172.J 190.r
Spencer mapping (map), Kodaira- 72.G
Spencer, Domina Eberle 130.r
Spencer, Donald Clayton 12.B 15.F 72.G r r C
Spencer, Thomas 402.G
Sperner, Emanuel 7.r 256.r 343.r 350.r
Sphere  -(of a point) 273.C -(of a point) 273.C
Sphere bundle n- 147.K
Sphere bundle n- cotangential 274.E
Sphere bundle n- normal 274.E
Sphere bundle n- tangential 274.E
Sphere bundle n- unit tangent 126.L
Sphere circumscribing (of a simplex) 139.I
Sphere combinatorial, group of oriented differentiable structures on the 114.I
Sphere complex 74.D
Sphere exotic 114.B
Sphere geometry 76.C
Sphere homotopy n- 65.C
Sphere homotopy n-, h-cobordism group of 114.I
Sphere horned, Alexander’s 65.G
Sphere open 140
Sphere open n- 140
Sphere pair 235.G 65.D
Sphere PL (k-1)- 65.C
Sphere pseudo- 111.I
Sphere Riemann 74.D
Sphere solid 140
Sphere solid n- 140
Sphere spectrum 202.T
Sphere theorem (characterization of a sphere) 178.C
Sphere theorem (embedding in a 3-manifold) 65.E
Sphere topological 140
Sphere topological solid 140
Sphere unit 140
Sphere w- 74.D
Sphere z- 74.D
Sphere(s) 139.I 150
Spherical (real hypersurface) 344.C
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




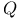
 -Hermitian form)
-Hermitian form)  - (of a divisor of an algebraic curve)
- (of a divisor of an algebraic curve)