|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
Set infinite 49.F 381.A
Set information 173.B
Set initial (of a correspondence) 358.B
Set initial (of a linear operator) 251.E
Set interior cluster 62.A
Set internally stable 186.I
Set interpolating (for a function algebra) 164.D
Set Kronecker 192.R
Set lattice of 243.E
Set lattice-ordered 243.A
Set Lebesgue measurable 270.G
Set Lebesgue measurable (of 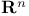 ) 270.G ) 270.G
Set level 279.D
Set limit 234.A
Set locally closed 425.J
Set M- 159.J
Set meager 425.N
Set minimal 126.E
Set n-cylinder 270.H
Set nilpotent (of a ring) 368.B
Set nodal 391.H
Set nonmeager 425.N
Set nonsaddle 120.E
Set nonwandering 126.E
Set nowhere dense 425.N
Set null 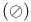 381.A 381.A
Set null (in a measure space) 270.D 310.I
Set null, of class JVS 169.E
Set of analyticity 192.N
Set of antisymmetry 164.E
Set of degeneracy (of a holomorphic mapping between analytic spaces) 23.C
Set of multiplicity 159.J
Set of points of indeterminacy (of a proper meromorphic mapping) 23.D
Set of quasi-analytic functions 58.F
Set of the first category 425.N
Set of the first kind 319.B
Set of the second category 425.N
Set of the second kind 319.B
Set of uniqueness 159.J
Set open 425.B
Set ordinate 221.E
Set orthogonal (of a Hilbert space) 197.C
Set orthogonal (of a ring) 368.B
Set orthogonal (of functions) 317.A
Set orthonormal (of a Hilbert space) 197.C
Set orthonormal (of functions) 317.A
Set P-convex (for a differential operator) 112.C
Set peak 164.D
Set perfect 425.O
Set point 381.B
Set polar (in potential theory) 261.D 338.H
Set power 381.B
Set precompact (in a metric space) 273.B
Set principal analytic 23.B
Set projective, of class n 22.D
Set purely d-dimensional analytic 23.B
Set quotient (with respect to an equivalence relation) 135.B
Set ratio 136.F
Set recurrent 260.E
Set recursive 356.D
Set recursively enumerable 356.D
Set regularly convex 89.G
Set relative closed 425.J
Set relatively compact 425.S
Set relatively compact (in a metric space) 273.F
Set relatively open 425.J
Set removable (for a family of functions) 169.C
Set residual 126.H 425.N
Set resolvent (of a closed operator) 251.F
Set resolvent (of a linear operator) 390.A
Set S- 308.I
Set saddle 126.E
Set scattered 425.O
Set semipolar 261.D
Set Sidon 192.R 194.R
Set sieved 22.B
Set singularity (of a proper meromorphic mapping) 23.D
Set stable 173.D
Set stable, externally 186.I
Set stable, internally 186.I
Set standard 22.I
Set strongly F-convex 112.C
Set strongly separated convex 89.A
Set system of closed 425.B
Set system of open 425.B
Set ternary 79.D
Set theory 381.F
Set theory axiomatic 33156.E
Set theory Bernays — Godel 33.A C
Set theory Boolean-valued 33.E
Set theory classical descriptive 356.H
Set theory effective descriptive 356.H
Set theory general 33.B
Set theory Godel 33.C
Set theory Zermelo 33.B
Set theory Zermelo — Fraenkel 33.A B
Set thin (in potential theory) 261.D
Set totally bounded (in a metric space) 273.B
Set totally bounded (in a uniform space) 436.H
Set U- 159.J
Set universal (for the projective sets of class n) 22.E
Set universal (of set theory) 381.B
Set wandering (under a measurable transformation) 136.C
Set wave front 274.B 345.A
Set wave front, analytic 274.D
Set weakly wandering 136.C
Set weakly wandering (under a group) 136.F
Set well-ordered 311.C
Set Z- 382.B
Set Zariski closed 16.A
Set Zariski dense 16.A
Set Zariski open 16.A
Set(s) 381
Set-theoretic formula 33.B
Set-theoretic topology 426
Sevast’yanov, Boris Aleksandrovich 44.r
Severi group, Neron- (of a variety) 16.P
Severi group, Neron-(of a surface) 15.D
Severi, Francesco 9.F r D F
Sewell inequality, Roepstorff — Araki- 402.G
Sewell, Geoffrey Leon 402.G
Sewell, Walter Edwin 336.H
Sgarro, Andrea 213.r
sgn P(sign) 103.A
Shabat, Aleksei Borisovich 387.F
Shadow costs 292.C
Shadow price 255.B
Shafarevich group, Tate- 118.D
Shafarevich reciprocity law 257.H
Shafarevich, Igor’ Rostislavovich 14.r 15.r 16.r 59.F H E S
Shallow water wave 205.F
Shampine, Lawrence Fred 303.r
Shaneson, Julius L. 65.D 114.J K r
Shanks, Daniel 332.r
Shanks, E. B. 109.r
Shanks, William 332
Shannon, Claude Elwood 31.C 136.E 213.A D-F403.r
Shannon, Robert E. 385.r
Shape category 382.A
Shape dominate 382.A
Shape function 223.G
Shape group 382.C
Shape invariant(s) 382.C
Shape morphism 382.A
Shape pointed 382.A
Shape same 382.A
Shape theory 382
Shapiro — Lopatinskii condition 323.H
Shapiro, Harold N. 123.D
Shapiro, Harold S. 43.r
| Shapiro, Harvey L. 425.r
Shapiro, Jeremy F. 215.r 264.r
Shapiro, Zoya Yakovlevna 258.r 323.H
Shapley value 173.D
Shapley, Lloyd Stowell 173.D E
Sharkovskii, Aleksandr Nikolaevich 126.N
Sharpe, Michael J. 262.r
Shaw H. 75.r
Shaw, B. 251.K
Shchegol’kov (Stschegolkow), Evgenii Alekseevich 22.r
Sheaf (sheaves) 383
Sheaf (sheaves) (in etale (Grothendieck) topology) 16.AA
Sheaf (sheaves) analytic 72.E
Sheaf (sheaves) associated with a presheaf 383.C
Sheaf (sheaves) Cech cohomology group with coefficient 383.F
Sheaf (sheaves) coherent algebraic 16.E 72.F
Sheaf (sheaves) coherent analytic 72.E
Sheaf (sheaves) coherent, of rings 16.E
Sheaf (sheaves) cohomology group with coefficient 383.E
Sheaf (sheaves) constant 383.D
Sheaf (sheaves) constructible 16.AA
Sheaf (sheaves) derived 125.W
Sheaf (sheaves) flabby 383.E
Sheaf (sheaves) invertible 16.E
Sheaf (sheaves) locally constructible (constant) 16.AA
Sheaf (sheaves) of 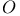 -modules 383.I -modules 383.I
Sheaf (sheaves) of Abelian groups 383.B
Sheaf (sheaves) of germs of analytic functions 383.D
Sheaf (sheaves) of germs of analytic mapping 383.D
Sheaf (sheaves) of germs of continuous functions 383.D
Sheaf (sheaves) of germs of differentiable sections of a vector bundle 383.D
Sheaf (sheaves) of germs of differential forms of degree of r 383.D
Sheaf (sheaves) of germs of functions of class  383.D 383.D
Sheaf (sheaves) of germs of holomorphic functions (on an analytic manifold) 383.D
Sheaf (sheaves) of germs of holomorphic functions (on an analytic set) 23.C
Sheaf (sheaves) of germs of holomorphic functions (on an analytic space) 23.C
Sheaf (sheaves) of germs of regular functions 16.B
Sheaf (sheaves) of germs of sections of a vector bundle 383.D
Sheaf (sheaves) of groups 383.C
Sheaf (sheaves) of ideals of a divisor (of a complex manifold) 72.F
Sheaf (sheaves) of rings 383.C
Sheaf (sheaves) orientation 201.R
Sheaf (sheaves) pre- 383.A
Sheaf (sheaves) pre-, on a site 16.AA
Sheaf (sheaves) scattered 383.E
Sheaf (sheaves) structure (of a prealgebraic variety) 16.C
Sheaf (sheaves) structure (of a ringed space) 383.H
Sheaf (sheaves) structure (of a variety) 16.B
Sheaf (sheaves) trivial 383.D
Sheaf space 383.C
Shear viscosity, coefficient of 205.C
Shear, modules of elasticity in 271.G
Shearing strain 271.G
Shearing stress 271.G
Sheet hyperboloid of revolution of one 350.B
Sheet hyperboloid of revolution of two 350.B
Sheet hyperboloid of two 350.B
Sheet mean number of (of a covering surface of a Riemann sphere) 272.J
Sheet number of (of a covering surface) 367.B
Sheet number of (of an analytic covering space) 23.E
Sheet(s) hyperboloid of one 350.B
Sheeted, n- 367.B
Shelah isomorphism theorem, Keisler- 276.E
Shelah, Saharon 33.r 276.E F r
Shelly, Maynard Wolfe 227.r
Shelukhin, V.V. 204.F
Shen Chao-Liang 36.H
Shenk, Norman A.,H. 112.P
Shepard, Roger Newland 346.E r
Sher, Richard B. 382.D
Sherman, Seymour 212.A r
Shewhart, Walter Andrew 401.G 404.A B
Shiba, Masakazu 367.I
Shibagaki, Wasao 174.r App. A Table
Shidlovskii, Andrei Borisovich 430.D r
Shields — Zeller theorem, Brown- 43.C
Shields, Allen Lowell 43.G r
Shields, Paul C. 136.E r
Shift 251.O
Shift associated with the stationary process 136.D
Shift automorphism 126.J
Shift Bernoulli 136.D
Shift generalized Bernoulli 136.D
Shift Markov 136.D
Shift operator 223.C 251.O 306.C
Shift operator unilateral 390.I
Shift phase 375.E 386.B
Shift transformation 136.D
Shiga, Kiyoshi 195.r
Shiga, Koji 72.r 147.O
Shige-eda, Shinsei 96.r
Shikata, Yoshihiro 178.r
Shilov boundary (for a function algebra) 164.C
Shilov boundary (of a domain) 21.D
Shilov boundary (of a Siegel domain) 384.D
Shilov generalized function, Gel’fand- 125.S
Shilov, Georgii Evgen’evich 21.D 36.M 125.A Q S
Shimada, Nobuo 114.B 202.S
Shimakura, Norio 323.H N
Shimidt (Schmidt), Otto Yul’evich 190.L 277.I
Shimizu, Hideo 32.H 450.L r
Shimizu, Ryoichi 374.H
Shimizu, Tatsujiro 124.B 272.J
Shimodaira, Kazuo 230.r
Shimura, Goro 3.M r F H r r r L M S U r
Shintani, Hisayoshi 303.r
Shintani, Takuro 450.A E G V r
Shioda, Tetsuji 450.Q S
Shiohama, Katsuhiro 178.r
Shiraiwa, Kenichi 126.J
Shirkov, Dmitril Vasil’evich 150.r 361.r
Shiryaev, Al’bert Nikolaevich 86.E 395.r 405.r
Shisha, Oved 211.r
Shizuta, Yasushi 41.D 112.P
Shmul’yan theorem 424.V
Shmul’yan theorem Eberlein- 37.G
Shmul’yan theorem Krein- 37.E 424.O
Shmul’yan, Yu.V. 37.E G V
Shnider, Steven David 344.C-E
Shnirel’man theory, Lyusternik- 286.Q
Shnirel’man, Lev Genrikhovich 4.A 279.G 286.Q r
Shock wave 205.B 446
Shoda, Kenjiro 8 29.F
Shoenfield, Joseph Robert 22. F H r
Shohat, James Alexander 240.r 341.r
Short exact sequence 200.I
Short international notation 92.E
Short range 375.B
Shortening 186.E
Shortest representation (of an ideal) 67.F
Shortest-path problem 281.C
Shortley, George H. 353.r
Shrelder, Yulii Anatol’evich 192.r
Shrikhande square 102.K
Shrikhande, S.S. 102.K 241.B STR
Shrinking (a space to a point) 202.E
Shub, Michael 126.J K r
Shubik, Martin 173.r
Shubnikov, Aleksei Vasil’evich 92.F r
Shult, Ernest E. 151.J
Shultz, Frederic W. 351.L
Shunt left 115.B
Shunt right 115.B
Shvarts (Schwarz, Svarc), Al’bert Solomonovich 56.H 80.r 286.D
SI(international system of units) 414.A
Sibuya, Yasutaka 289.D E r
Sidak, Zbynek 371.r
Side 155.B F
Side (of a complete quadrangle) 343.C
Side (of a point with respect to a hyperplane) 7.D
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



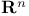 )
) 
 -modules
-modules 