|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
Projective curvature tensor App. A Table
Projective deformation (between surfaces) 110.B
Projective determinacy 22.H
Projective differential geometry 110.B
Projective dimension (of a module) 200.K
Projective frame (in projective geometry) 343.C
Projective general linear group 60.B
Projective general linear group of degree n over K 60.B
Projective geometry 343
Projective geometry finite-dimensional 343.B
Projective geometry fundamental theorem of 343.D
Projective geometry general 343.B
Projective geometry of paths 109
Projective limit (in a category) 210.D
Projective limit (of a projective system of sets) 210.B
Projective limit (of a projective system of topological groups) 423.K
Projective limit group 210.C
Projective limit space 210.C
Projective line 343.B
Projective line element 110.B
Projective mapping (in projective geometry) 343.B
Projective module, (R, S)- 200.K
Projective morphism 16.E
Projective morphism quasi- 16.E
Projective plane 343.B
Projective plane Cayley 54
Projective plane finite 241.B
Projective representation (of a group) 362.J
Projective representation irreducible 362.J
Projective representation similar 362.J
Projective resolution 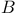 - 200.Q - 200.Q
Projective resolution (in an Abelian category) 200.I
Projective resolution left (ofanzl-module) 200.C
Projective scheme 16.E
Projective scheme quasi- 16.E
Projective set of class n 22.D
Projective space 343.B
Projective space complex 343.D
Projective space infinite-dimensional complex 56.C
Projective space infinite-dimensional real 56.B
Projective space left 343.F
Projective space over A 147.E
Projective space real 343.D
Projective space right 343.F
Projective special linear group 60.B
Projective special linear group (over a noncommutative field) 60.0
Projective special unitary group over K 60.H
Projective symplectic group over K 60.L
Projective system (in a category) 210.D
Projective system (of groups) 210.C
Projective system (of sets) 210.B
Projective system (of toplogical spaces) 210.C
Projective system (of topological groups) 423.K
Projective topology 424.R
Projective transformation 343.D 364.F
Projective transformation group 343.D
Projective transformation group of 343.D
Projective transformation regular 343.D
Projective transformation singular 343.D
Projective transformation singular, of the kth species 343.D
Projective unitary group 60.F
Projective variety 16.A
Projectively flat space App. A Table
Projectively related (fundamental figures) 343.B
Prokhorov, Yurii Vasil’evich 115.D 250.E r341.F r374.r
Prolate App. A Table
Proliferation (of errors) 138.D
Prolongable (Riemann surface) 367.F
Prolongation (along a curve in a covering surface) 367.B
Prolongation (of a Riemann surface) 367.F
Prolongation (of a solution of an ordinary differential equation) 316.C
Prolongation (of a system of partial differential equations) 428.B F
Prolongation (of a valuation) 439.B
Prolongation analytic 198.G
Prolongation fcth (of G) 191.D
Prolongation first (of P) 191.E
Prolongation kth (of a Lie subalgebra) 191.D
Prolongation kth (of P) 191.E
Prolongational limit set first negative 126.D
Prolongational limit set first positive 126.D
Proof theory 156.D
Proof, consistency 156.D
Proof, consistency for pure number theory 156.E
Propagation equation of sound 325.A
Propagation of chaos 340.F
Propagation of errors 138.C
Propagation of singularities 325.M
Propagation wave 446
Proper (continuous mapping) 425.W
Proper (equivalence relation in an analytic space) 23.E
Proper (leaf) 154.D
Proper (Lorentz group) 258.A
Proper (morphism of scheme) 16.D
Proper (PL embedding) 65.D
Proper affine transformation 7.E
Proper class (in set theory) 381.G
Proper complex Lorentz group 258.A
Proper component (of an intersection of subvarieties) 16.G
Proper convex function 88.D
Proper factor (of an element of a ring) 67.H
Proper flag manifold 199.B
Proper function (of a boundary value problem) 315.B
Proper hypersphere (in hyperbolic geometry) 285.C
Proper Lorentz group 60.J
Proper mapping fundamental theorem of 16.X
Proper mapping(s) 425.W
Proper meromorphic mapping (between analytic spaces) 23.D
Proper modification (of an analytic space) 23.D
Proper motion in Euclidean geometry 139.B
Proper motion of a star 392
Proper orthogonal group 60.I258.A
Proper orthogonal matrix 269.J
Proper product (of two normal 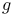 -lattices) 27.A -lattices) 27.A
Proper quadric surface 350.B
Proper rotation group 258.A
Proper subset 381.A
Proper time 258.A
Proper transform (of a subvariety) 16.I
Proper value (of a boundary value problem) 315.B
Proper value (of a linear mapping) 269.L
Proper value (of a linear operator) 390.A
Proper value (of a matrix) 269.F
Proper variation 279.F
Proper vector (belonging to an eigenvalue) 269.F
Proper vector (of a linear operator) 390.A
Proper vector (of a linear transformation) 269.L
Properly (n — l)-dimensional quadric hypersurface 350.G
Properly convex (subset of a sphere) 274.E
Properly discontinuous transformation group 122.A
Properly divergent 379.A
Properly equivalent (binary quadratic forms) 348.M
Properly infinite 308.E
Properly intersect (on a variety) 16.G
Properly posed (initial value problem) 321.E
Properly posed (problems for partial differential equations) 322.A
Property (properties) 411.G
Property (properties) approximation 37.L
Property (properties) asymptotic (of solutions of a system of linear ordinary differential equations) 314.A
Property (properties) Baire 425.N
Property (properties) basic (of a structure) 409.B
Property (properties) bounded approximation 37.L
Property (properties) clustering 402.G
Property (properties) combinatorial 65.A
Property (properties) continuity, for Cech theory 201.M
Property (properties) countably productive 425.Y
Property (properties) covering homotopy 148.B
Property (properties) duality (of linear spaces) 256.G
Property (properties) equivalence 135.A
Property (properties) finite intersection 425.S
Property (properties) finite subset 396.F
| Property (properties) global (in differential geometry) 109
Property (properties) homotopy extension 202.E
Property (properties) in the large (in differential geometry) 109
Property (properties) in the small (in differential geometry) 109
Property (properties) local (in differential geometry) 109
Property (properties) local (of a pseudodifferential operator) 345.A
Property (properties) Markov 261.B
Property (properties) micro-pseudolocal (of a pseudodifferential operator) 345.A
Property (properties) minimum curvature 223.F
Property (properties) minimum norm 223.F
Property (properties) of continuity (in a continuous geometry) 85.A
Property (properties) P conjecture 235.B
Property (properties) pseudo-orbit tracing 126.J
Property (properties) pseudolocal (of a pseudodifferential operator) 345.A
Property (properties) reproducing (of a probability distribution) 341.E App. Table
Property (properties) spectral 136.E
Property (properties) star-finite 425.S
Property (properties) strong Markov 261.B
Property (properties) topological 425.G
Property (properties) uniformity 399.N
Property (properties) universal mapping 52.L
Proposition modal 411.L
Proposition universal 411.B
Proposition variables 411.E
Proposition(s) existential 411.B
Propositional calculus 411.F
Propositional connectives 411.E
Propositional function 411.C
Propositional logic 411.E
Protter, Murray H. 78.r 110.r 216.r 323.r 327.r 350.r
Provable (formula) 411.I
Proximity function (of a meromorphic function) 272.B
Prufer ring 200.K
Prugovecki, Eduard 375.r
Przymusinski, TeodorC. 117.E
Przytycki, Feliks 126.K
Pseudo — Runge — Kutta method 303.D
Pseudo-arc 79.D
Pseudo-Hermitian manifold 344.F
Pseudo-isotopic 65.D
Pseudo-isotopy 65.D
Pseudo-orbit 126.J
Pseudo-orbit  - 126.J - 126.J
Pseudo-orbit tracing property 126.J
Pseudo-ordering 311.H
Pseudo-Riemannian metric 105.P
Pseudoanalytic function, K- 352.B
Pseudocompact (space) 425.S
Pseudoconformal geometry 344.A
Pseudoconformal transformation 344.A
Pseudoconformally equivalent 344.A
Pseudoconvex (domain) 21.G
Pseudoconvex (domain) Cartan 21.I
Pseudoconvex (domain) d- 21.G
Pseudoconvex (domain) Levi 21.I
Pseudoconvex (domain) locally Cartan 21.I
Pseudoconvex (domain) locally Levi 21.I
Pseudoconvex (domain) strictly 344.A
Pseudoconvex (domain) strongly 21.G
Pseudodifferential operator 251.O 274.F 345
Pseudodistance Caratheodory 21.O
Pseudodistance function 273.B
Pseudodistance Kobayashi 21.O
Pseudofunction 125.C
Pseudogeometric ring 284.F
Pseudogroup (of topological transformations) 105.Y
Pseudogroup (of topological transformations) of transformations (on a topological space) 90.D
Pseudogroup structure 105.Y
Pseudointerior 382.B
Pseudolocal property (of a pseudodifferential operator) 345.A
Pseudolocal property (of a pseudodifferential operator) micro- 345.A
Pseudomanifold 65.B
Pseudometric 273.B
Pseudometric space 273.B
Pseudometric space indiscrete 273.B
Pseudometric uniformity 436.F
Pseudometrizable 436.F
Pseudonorm (on a topological linear space) 37.O 424.F
Pseudopolynomial, distinguished 21.E
Pseudorandom numbers 354.B
Pseudosphere 111.I285.E
Pseudotensorial form 80.G
Pseudovaluation 439.K
Pseudovaluation  -collective 354.E -collective 354.E
Psi function 174.B
PSL(n, k) (projective special linear group) 60.B
Psychometrics 346
Ptak, Vlastimil 424.X
pth power operation Pontryagin 64.B
pth power operation Steenrod 64.B
pth power, operator of summable 68.K
Ptolemy 187 432.C
PU(n) (projective unitary group) 60.F
Pugh, Charles C 126.J-L r
Puiseux series 339.A
Puiseux, Victor Alexandre 339.A
Pukanszky, Lajos 437.K U
Pullback (of a differential form) 105.Q
Pullback (of a distribution) 125.Q
Pullback (of a divisor) 16.M
Puppe exact sequence 202.G
Puppe, Dieter 200.r 202.G
Pure 136.E
Pure (continued fraction) 83.C
Pure (differential form) 367.H
Pure (state) 351.B
Pure geometry 181
Pure ideal 284.D
Pure integer programming problem 215.A
Pure number theory 156.E
Pure periodic continued fraction 83.C
Pure phase 402.G
Pure point spectrum 136.E
Pure strategy 173.B
Purely contractive 251.N
Purely contractive part 251.N
Purely d-dimensional analytic set 23.B
Purely d-dimensional analytic set (at a point) 23.B
Purely discontinuous distribution 341.D
Purely imaginary number 74.A
Purely infinite (von Neumann algebra) 308.E
Purely inseparable (extension of a field) 149.H
Purely inseparable (rational mapping) 16.I
Purely inseparable element (of a field) 149.H
Purely n-codimensional 125.W
Purely nondeterministic 395.D
Purely transcendental extension 149.K
Puri, MadanLai 280.r 371.r
Pursuit, curve of 93.H
Push-down automaton 31.D
Push-down storage 96.E
Pustyl’nik, Evgenii Izievich 251.r
Pusz, Wieslaw 402.G
Putnam, Calvin Richard 251.K
Putnam, Hilary Whitehall 81.D r r
Putnam’s theorem 251.K
Pyatetskii — Shapiro reciprocity law, Gel’fand 437.DD
Pyatetskii-Shapiro, Il’ya losifovich 32.H 122.G 125.r 159.J 384.A C r S
Pythagoras 60.O 118 A 139.B D
Pythagorean closure (of a field) 155.C
Pythagorean extension (of a field) 155.C
Pythagorean field 139.B 155.C
Pythagorean number 145
Pythagorean ordered field 60.O
Pythagorean Theorem 139.D
Q (rational numbers) 294.A D
q-block bundle 147.Q
q-block structure 147.Q
q-boundary 201.B
q-chains 201.B
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -
-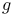 -lattices)
-lattices)  -
-  -collective
-collective