|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
Third fundamental form App. A Table
Third homotopy theorem (in the theory of obstructions) 305.C
Third isomorphism theorem (on topological groups) 423.J
Third kind Abelian differential of 11.C
Third kind Abelian integral of 11.C
Third law of thermodynamics 419.A
Third quartiles 396.C
Third separation axiom 425.Q
Third-order predicate logic 411.K
Thirring, Walter Eduard 212.B
Thom complex 114.G
Thom complex associated with (G, n) 114.G
Thom first isotropy theorem 418.G
Thom fundamental theorem 114.H
Thom space 114.G
Thom spectrum, stable homotopy group of 114.G 202.T
Thom — Gysin isomorphism 114.G
Thom — Gysin isomorphism (on a fiber space) 148.E
Thoma, Elmar Herbert 437.E
Thomas Aquinas 372
Thomas, J. 206.C
Thomas, Lawrence E. 375.F
Thomas, Paul Emery 64.r
Thomas, Richard Kenneth 136.E
Thomas, Tracy Yerkes 152.C
Thomason, Steven Karl 22.F
Thompson inequality, Golden- 212.B
Thompson theorem, Feit- (on finite groups) 151.D
Thompson, Colin John 212.B
Thompson, John Griggs 151.D H-J
Thompson.J.F. 304.E
Thomsen, Gerhard 155.H
Thorin theorem, Riesz- 224.A
Thorin, G.O. 88.r 224.A
Thorn (of a convergence domain) 21.B
Thorn algebra 114.H
Thorn, Rene F. 12.B 51.A B E F r F-H H M r
Thorne, Kip S. 359.r
Thorpe, J.A. 91.r
Thrall, Robert McDowell 29.r 173.D 368.r
Three big problems 187
Three laws of motion, Newton’s 271.A
Three principles, Fisher’s 102.A
Three-body problem 420.A
Three-body problem restricted 420.F
Three-circle theorem, Hadamard 43.E
Three-line theorem, Doetsch 43.E
Three-series theorem 342.D
Three-stage least squares method 128.C
Three-valued logic 411.L
Threlfall, William 65.r 91.r 99.r 170.r 201.r 235.r 410.r
Threshold Jacobi method 298.B
Thue problem 31.B
Thue theorem 118.D
Thue, Axel 31.B 118.D 182.G
Thullen theorem, Cartan- 21.H
Thullen, Peter 20 21.H M Q
Thurston, William P. 65.E 126.J N D-H r E
Thurstone — Mosteller model 346.C
Thurstone, Louis Leon 346.C F
Tierney, Myles 200.r
Tieset 186.G
Tieset matrix, fundamental 186.G
Tietavainen, Aimo A. 63.r
Tietze extension theorem 425.Q
Tietze first axiom 425.Q
Tietze second axiom 425.Q
Tietze, Heinrich 425.Q
Tight family (of probability measures) 341.F
Tight immersion 365.O
Tightness 399.M
Tikhonov embedding theorem 425.T
Tikhonov fixed-point theorem 153.D
Tikhonov product theorem 425.S
Tikhonov separation axiom 425.Q
Tikhonov space 425.Q
Tikhonov theorem 425.Q
Tikhonov theorem Uryson- (on metrizability) 273.K
Tikhonov — Uryson theorem 425.Q
Tikhonov, Andrei Nikolaevich 153.D 273.K 425.Q S T
Time change (of a Markov process) 261.B
Time change (of a semimartingale) 406.B
Time change (of a submartingale) 262.C
Time complexity 71.A
Time exit 261.B
Time explosion 406.D
Time first splitting 44.E
Time hitting 260.B 261.B 407.B
Time killing 260.A
Time life 260.A 261.B
Time local 45.G
Time Markov 261.B 407.B
Time NP- 71.E
Time optimal control problem 86.F
Time ordered function 150.D
Time parameter (of a stochastic process) 407.A
Time parameter space 260.A
Time polynomial 71.E
Time proper 258.A
Time real- 19.E
Time recurrence 260.C
Time reversal 258.A 359.B
Time series 397.A 421.A
Time series analysis 421
Time series data 397.N
Time sojourn, density 45.G
Time stopping 261.B 407.B
Time terminal 261.B
Time waiting 260.H
Time waiting, distribution 307.C
Time-dependent Schrodinger equation 351.D
Time-homogeneous Markovian type 406.D
Time-independent Markovian type 406.D
Time-independent Schrodinger equation 351.D
Time-invariant network 282.C
Time-invariant, linear (dynamical systems) 86.B
Time-one mapping (map) 126.C
Time-varying system, linear 86.B
Timelike (curve) 325.A
Timelike (vector of a Minkowski space) 258.A 359.B
Timmesfeld, Franz-Georg 151.J
Timoshenko, Stephen P. 271.r
Tisserand, Francois Felix 55.r
Tissot — Pochhammer differential equation 206.C
Tissot, Nicolas Auguste 206.C
Titchmarsh theorem 306.B
Titchmarsh theorem Brun- 123.D
Titchmarsh — Kodaira theory, Weyl- Stone- 112.O
Titchmarsh, Edward Charles 112.O 123.B D r r r
Tits simple group 151.I
Tits system 13.R 151.J 343.I
Tits, Jacques Leon 13.O Q R r J
TM waves 130.B
Toda bracket 202.R
Toda lattice 287.A 387.A
Toda, Hirosi 202.P R U
Toda, Morikazu 287.A r
Toda, Nobushige 17.C
Todd characteristic 366.B
Todd class (of a complex vector bundle) 237.F
Todd, John Arthur 237.F 366.B r
Todhunter, Isaac 342.r
Todorov, Andrei Nikolov 232.C
Todorov, Ivan T. 146.r 150.r
Toeplitz operator 251.O
Toeplitz theorem 379.L
Toeplitz, Otto 197.r 217.r 251.O 379.L
Toki, Yukinari 62.D 352.A 367.E
Tolerance interval 399.R
Tolerance limits 399.R
| Tolerance percent defective, lot 404.C
Tolerance region 399.R
Tollmien, Walter 433.A
Tolman, Richard Chace 402.r
Tolstoy, I. 446.r
Tomi, Friedrich 275.C
Tomita — Takesaki theory 308.H
Tomita, Minoru 308.H
Tomiyama, Jun 36.K 164.E
Tomonaga, Sin-itiro 132.C 146.A 150.A 359.C 361.A
Tomotika, Susumu 134.r
Tompkins, Charles Brown 275.B 365.B
Tondeur, Philippe Maurice 154.G H r
Tonelli absolutely continuous in the sense of 246.C
Tonelli bounded variation in the sense of 246.C
Tonelli, Leonida 107.A246.C
Tonnelat-Baudot, Marie-Antoinette 434.r
Topological  -algebra 270.C -algebra 270.C
Topological Abelian group dual 422.C
Topological Abelian group elementary 422.E
Topological Abelian group(s) 422
Topological conjugacy 126.B
Topological entropy 126.K 136.H
Topological equivalence 126.B
Topological field 423.P
Topological generator (of a compact Abelian group) 136.D
Topological group 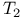 - 423.B - 423.B
Topological group completable 423.H
Topological group complete 423.H
Topological group Hausdorff 423.B
Topological group homomorphic 423.J
Topological group isomorphic 423.A
Topological group locally isomorphic 423.0
Topological group metrizable 423.I
Topological group separated 423.B
Topological group(s) 423
Topological groupoid 154.C
Topological index (of an elliptic complex) 237.H
Topological invariance (of homology groups) 201.A
Topological invariant 425.G
Topological linear spaces 424
Topological manifold 105.B
Topological manifold with boundary 105.B
Topological manifold without boundary 105.B
Topological mapping 425.G
Topological n-cell 140
Topological pair 201.L
Topological polyhedron 65.A
Topological pressure 136.H
Topological property 425.G
Topological ring 423.P
Topological solid sphere 140
Topological space category of 52.B
Topological space category of pointed 202.B
Topological space complex linear 424.A
Topological space discrete 425.C
Topological space generalized 425.D
Topological space homotopy category of 52.B
Topological space inductive system of 210.C
Topological space linear 424.A
Topological space metrizable 273.K
Topological space product 425.K
Topological space projective system of 210.C
Topological space quotient 425.L
Topological space real linear 424.A
Topological space underlying (of a complex manifold) 72.A
Topological space underlying (of a differentiable manifold) 105.D
Topological space underlying (of a topological group) 423.A
Topological space uniform 436.C
Topological space uniformizable 436.H
Topological space(s) 425
Topological sphere 140
Topological structure 425.A B
Topological sum 425.M
Topological transformation group 431.A
Topological vector space 424.A
Topologically complete space 436.I
Topologically conjugate 126.B
Topologically equivalent 126.B H
topology 425.B 426
Topology  -adic (of an R-module) 284.B -adic (of an R-module) 284.B
Topology  (on the tensor product of locally convex spaces) 424.R (on the tensor product of locally convex spaces) 424.R
Topology  -weak 308.B -weak 308.B
Topology  (on the tensor product of locally convex spaces) 424.R (on the tensor product of locally convex spaces) 424.R
Topology algebraic 426
Topology base for a 425.F
Topology box 425.K
Topology coarser 425.H
Topology combinatorial 426
Topology compact-open 279.C 435.D
Topology compact-open  279.C 279.C
Topology differential 114
Topology discrete 425.C
Topology etale 16.AA
Topology fine (on a class of measures) 261.D 338.E
Topology finer 425.H
Topology Gel’fand 36.E
Topology general 426
Topology hereditarily weak 425.M
Topology hull-kernel 36.D
Topology I-adic (of a ring) 16.X
Topology indiscrete 425.C
Topology induced 425.I
Topology induced by a mapping 425.I
Topology inner (of a Lie subgroup) 249.E
Topology Jacobson 36.D
Topology Krull (for an infinite Galois group) 172.I
Topology larger 425.H
Topology leaf 154.D
Topology linear 422.L
Topology Mackey 424.N
Topology metric 425.C
Topology of biequicontinuous convergence 424.R
Topology of Lie groups and homogeneous spaces 427
Topology of surfaces, fundamental theorem of 410.B
Topology of the uniformity 436.C
Topology of uniform convergence 424.K
Topology order 425.C
Topology PL 65.A
Topology product 425.K
Topology projective 424.R
Topology quotient 425.L
Topology relative 425.J
Topology S- (on a linear space) 424.K
Topology Sazonov 341.J
Topology set-theoretic 426
Topology smaller 425.H
Topology strong (on a class of measures) 338.E
Topology strong (on a direct product space) 425.K
Topology strong (on a normed space) 37.E
Topology strong (on a topological linear space) 424.K
Topology strong operator 251.C
Topology stronger 425.H
Topology subbase for a 425.F
Topology trivial 425.C
Topology uniform 436.C
Topology uniform operator 251.C
Topology uniformizable 436.H
Topology vague (on a class of measures) 338.E
Topology weak  279.C 279.C
Topology weak (in a cell complex) 70.D
Topology weak (on a class of measures) 338.E
Topology weak (on a direct product space) 425.K
Topology weak (on a direct sum) 425.M
Topology weak (on a locally convex space) 424.H
Topology weak (on a normed linear space) 37.E
Topology weak operator 251.C
Topology weak* (on a locally convex space) 424.H
Topology weak* (on a normed space) 37.E
Topology weak, relative to the pairing <E, F> 424.H
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -algebra
-algebra 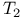 -
-  -adic (of an R-module)
-adic (of an R-module)  (on the tensor product of locally convex spaces)
(on the tensor product of locally convex spaces)  (on the tensor product of locally convex spaces)
(on the tensor product of locally convex spaces) 