|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
Vector lattice complete 310.C
Vector lattice normed 310.F
Vector line (of a vector field) 442.D
Vector mean 341.B
Vector mean curvature 365.D
Vector measure 443.G
Vector measure absolutely continuous 443.G
Vector measure bounded 443.G
Vector measure completely additive 443.G
Vector measure finitely additive 443.G
Vector normal 105.L. 111.H 364.A
Vector normalized 409.G
Vector observation 102.A
Vector orthogonal 139.G
Vector p- 256.O
Vector p-, bundle of 147.F
Vector positive 7.A 442.A
Vector potential 130.A 442.D
Vector Poynting 130.A
Vector product 442.C App. Table
Vector proper (of a linear mapping) 269.L
Vector proper (of a linear operator) 390.A
Vector proper (of a matrix) 269.F
Vector representation (of a Clifford group) 61.D
Vector root 390.B
Vector row 269.A
Vector space 442.A
Vector space metric 256.H
Vector space over a field 256.H
Vector space prehomogeneous 450.V
Vector space standard (of an affine space) 7.A
Vector space tangent 105.H
Vector space topological 424.A
Vector tangent 105.H
Vector tangent, holomorphic 72.A
Vector tangent, of type (0, 1) 72.C
Vector tangent, of type (1, 0) 72.C
Vector triple product 442.C App. Table
Vector tube 442.D
Vector unit 442.B
Vector unit (of an affine frame) 7.C
Vector vacuum 377.A
Vector valuation 6.C
Vector valuation, ring of 6.C
Vector vertical 80.B
Vector wave number (of a sine wave) 446
Vector Witt 449
Vector Witt, of length n 449.B
Vector zero 442.A
Vector(s) (in a Euclidean space) 442
Vector-valued integral 443
Vectorial form, canonical 417.C
Vectorial p-form 417.C
Vedesinov, N. 425.Q
Veech, William Austin 136.H
Vekua, Il’ya Nestorovich 217.J 323.r
Veldkamp, Ferdinando D. 13.R
Velo, Giorgio 150.r
Velocity group 446
Velocity phase (of a sine wave) 446
Velocity phase space 126.L
Velocity potential 205.B
Veneziano model 132.C 386.C
Veneziano, Gabriele 132.C 386.C
Venkov, Boris Borisovich 200.M
Venttsel’, Aleksandr Dmitrievich 115.C 261.r 406.F
Ver Eecke, Paul 187.r
Verbeure inequality, Roepstorff — Fannes- 402.G
Verbeure, Andre 402.G
Verbiest, Ferdinand 57.C
Verdier, Jean-Louis 16.r 450.Q r
Vergne, Michele 384.r
Verhulst, Pierre Francois 263.A
Verner, James Hamilton 303.r
Veronese surface 275.F
Veronese, Giuseppe 275.F
Versal (unfolding) 51.D
Vershik, Anatolil Moiseevich 136.D r
Version (of a stochastic process) 407.A
Vertex (in a cell complex) 70.D
Vertex (in a Euclidean (simplicial) complex) 70.B
Vertex (in a simplicial complex) 70.C
Vertex (in the polyhedron of a simplicial complex) 70.C
Vertex (of a circular cone) 78.A
Vertex (of a complete quadrangle) 343.C
Vertex (of a convex cell in an affine space) 7.D
Vertex (of a convex polyhedron) 89.A
Vertex (of a geodesic triangle) 178.A
Vertex (of a graph) 186.B
Vertex (of a linear graph) 282.A
Vertex (of a parabola) 78.C
Vertex (of a polygon) 155.F
Vertex (of a simplex in an affine space) 7.D
Vertex (of a spherical triangle) 432.B
Vertex (of a star region) 339.D
Vertex (vertices) (of an angle) 139.D 155.B
Vertex adjacent 186.B
Vertex end 186.B
Vertex initial 186.B
Vertex isolated 186.B
Vertex terminal 186.B
Vertical angles 139.D
Vertical component (of a vector field) 80.C
Vertical slit mapping, extremal 367.G
Vertical vector 80.B
Very ample (divisor) 16.N
Very ample (linear system) 16.N
Very ample (sheaf) 16.E
Very weak Bernoulli process 136.E
Vesentini, Edoarc 122.F
Vessiot extension field, Picard- 113
Vessiot theory, Picard- 113
Vessiot, Ernest 107.A 113 249.V
Vey classes, Godbillon- 154.G
Vey, Jacques 151.G r
Vibrating membrane, equation of a 325.A
Vibrating string, equation of a 325.A
Vibration 318
Vibration normal 318.B
Vibration parametrically sustained 318.B
Vibration self-excited 318.B
Vick, James 201.r
Viehweg, Eckart 72.I r r
Viete, F. 444
Viete, Francois 8 20 332 360 444
Vietoris axiom 425.Q
Vietoris exact sequence, Mayer- (for a proper triple) 201.C
Vietoris, Leopold 201.A C E L
Vigneras, Marie-France 391.C
Vigue, Jean-Pierre 384.r
Vilenkin, Naum Yakovlevich 112.r 125.r 162.r 218.r 341.r 389.r 395.r 407.C 437.AA
Villat integration formula App. A Table
Villat, Henri Rene Pierre App. A Table
Ville, Jean A. 262.A
Vinberg, Ernest Borisovich 122.G 351.I 384.C r
Vinogr Mov, Ivan M. 4.C E E
Vinogradov mean value theorem 4.E
Vinter, Richard B. 127.G
Virtanen, Kaarlo T. 62.C 352.A C I
Virtual arithmetic genus (of a divisor) 16.E
viscosity 205.B
Viscosity coefficient of 205.C
Viscosity coefficient of bulk 205.C
Viscosity coefficient of shear 205.C
Viscosity magnetic 259
Vishik, Mark Iosifovich 112.E 323.N
Visibility manifold 178.F
Vitali covering theorem 380.D
Vitali, Giuseppe 270.G 380.D
Viterbi, Andrew J. 213.E
| Vitt, Aleksandr Adol’fovich 290.r
Vitushkin, Anatolil Georgievich 164.J 169.E
Vivanti theorem 339.A
Vivanti, Giulio 217.r 339.A
Vladimirova, S.M. 365.J
Vogan, David Alexander, Jr. 437.r
Vogel, Kurt 24.r
Vogel, William R. 200.r
Vogt, Dietmar 168.B
Voichick, Michael 164.K
Voiculescu, Dan Virgil 36.J 331.E
Voider, J.E. 142.C
Voigt, Jurgen 331.E
Volk, Isai Mikhallovich 289.E
Volkov, Yurii Aleksandrovich 365.J
Volkovyskil, L. 198.r
Volterra integral equation 217.A
Volterra operator 68.J
Volterra theorem, Poincare- 198.J
Volterra type integral equation of 217.A
Volterra type integrodifferential equation of 222.A
Volterra, Vito 20 68.J 162 163.B 198.J 217.A 222.A 263.B
Voltyanskii, V.G. 155.r
Volume (of a lattice in a Euclidean space) 92.D
Volume (of a polyhedron) 139.F
Volume (of a simplex in an affine space) 7.E
Volume (ofanidele) 6.D
Volume element (of an oriented  -manifold) 105.W -manifold) 105.W
Volume element associated with a Riemannian metric 105.W
Volume element integral of a function with respect to a (on a  -manifold) 105.W -manifold) 105.W
Volume inner 270.G
Volume outer 270.G
von Eotvos, Roland 359.D
von Helmholtz, Hermann 139.A 188.D 205.B 419.C 442.D App. A Tables 15.VI
von Karman transonic similarity 205.D
von Karman, Theodore 205.E 433.C
von Koch, Helge 246.K 450.I
von Mises theorem 399.K
von Mises, Richard 298.r 342.A 354.E 399.K r
von Neumann algebra 308.C
von Neumann algebra discrete 308.E
von Neumann algebra finite 308.E
von Neumann algebra induced 308.C
von Neumann algebra of type I 308.E
von Neumann algebra of type II 308.E
von Neumann algebra of type III 308.E
von Neumann algebra oftype 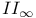 308.E 308.E
von Neumann algebra purely infinite 308.E
von Neumann algebra reduced 308.C
von Neumann algebra semifmite 308.E
von Neumann algebra structure theorem for, of type III 308.I
von Neumann condition 304.F
von Neumann density theorem 308.C
von Neumann inequality 251.M
von Neumann reduction theory 308.G
von Neumann selection theorem 22.F
von Neumann theorem, Weyl- 390.I
von Neumann uniqueness theorem 351.C
von Neumann — Halmos theorem 136.E
von Neumann — Morgenstern solution 173.D
von Neumann, J. 445
von Neumann, John 18.A E r r C B E F r C D r r F G I r L r
von Seidel, Philipp Ludwig 302.C
von Struve, Friedrich George Wilhelm 39.G App. A Table
Vopenka, Petr 33.r
Voronoi, Georgil Fedoseevich 242.A
Vortex line 205.B
Vortex, vector field without 442.D
Vorticity 205.B
Vorticity theorem, Helmholtz 205.B
Voss, Heinz-Jiirgen 186.r
Vossen theorem, Cohn- 111.I
Vranceanu, Gheorghe 434.C
VSVO algorithm 303.E
Vulikh, Boris Zakharovich 310.A
W*-algebra 308.C
W-construction (of an Eilenberg — MacLane complex) 70.F
w-plane 74.D
w-point (of an entire function) 429.B
w-sphere 74.D
W-surface 111.I
W.B.process 136.E
Wada, Junzo 164.C
Wada, Yasusi 230
Waelbroeck, Lucien 36.M
Wage, M.L. 117.E
Wagner function 39.F
Wagner, Harvey Maurice 307.r 408.r
Wagner, Herbert 39.F
Wagner, S.W. 95.r
Wagschal, Claude 321.G
Wagstaff, Samuel S. 14.L 145
Wahl, Jonathan Michael 9.r
Wahlin, G.E. 145.r *
Wait, R. 223.r 301.r 304.r
Waiting time 260.H
Waiting time distribution 307.C
Wakakuwa, Hidekiyo 13.F
Wald theorem 399.H M
Wald, Abraham 399.H M r r
Waldhausen, Friedhelm 65.E 235.B
Waldschmidt, Michel 430.D r
Wales, David B. 151.I App. B Table
Walfisz, Arnold Z. 4.D 123.D 220.B 242.r 295.D
Walker equation, Yule- 421.D
Walker metrics, Robertson- 359.E
Walker, Arthur G. 359.E
Walker, G. 421.D*
Walker, M.R. 376.r
Walker, R.C. 425.r
Walker, Robert John 9.r 15.B
Wall adiabatic 419.A
Wall diathermal 419.A
Wall group 114.J
Wall, Charles Terens Clegg 114.H J K r
Wallace, Andrew Hugh 114.F L
Wallach, Nolan R. 178.r 199.r 249.r 275.A F
Wallis formula App. A Table
Wallis test, Kruskal- 371.D
Wallis, Jennifer Seberry 241.r
Wallis, John 20 265 332 App. A Table
Wallis, Walter Denis 241.r
Wallis, Wilson Allen 371.D
Wallman, Henry 117.r
Walsh system of orthogonal functions 317.C
Walsh, John Joseph 117.I
Walsh, Joseph Leonard 223.r 317.C 336.F I
Walter, J.S. 142.C
Walter, John H. 151.J
Walter, Wolfgang 211.r
Walters, Peter 136.H
Walther, Hansjoachim 186.r
Wandering 126.E
Wandering point 126.E
Wandering set 136.C
Wang exact sequence (of a fiber space) 148.E
Wang Hsien-Chung 81 110.E 148.E 152.r 199.r 413.r
Wang Xiaotong 57.A
Wang, Ju-Kwei 164.G
Wantzel, Pierre-Laurent 179.A
Ward, Harold Nathaniel App. B Table R.I6.r
Waring problem 4.E
Waring, Edward 4.E
Warner, Frank Wilson 364.H
Warner, Garth William, Jr. 249.r 437.r
Warning second theorem 118.B
Warning theorem 118.B
Warning, E. 118.B
Warschawski, Stefan Emanuel 77.C
Wasan 230
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -manifold)
-manifold)