Àâòîðèçàöèÿ
Ïîèñê ïî óêàçàòåëÿì
Graham R.L., Grotschel M., Lovasz L. — Handbook of combinatorics (vol. 1)
Îáñóäèòå êíèãó íà íàó÷íîì ôîðóìå Íàøëè îïå÷àòêó?
Íàçâàíèå: Handbook of combinatorics (vol. 1)Àâòîðû: Graham R.L., Grotschel M., Lovasz L.Àííîòàöèÿ: Combinatorics research, the branch of mathematics that deals with the study of discrete, usually finite, structures, covers a wide range of problems not only in mathematics but also in the biological sciences, engineering, and computer science. The Handbook of Combinatorics brings together almost every aspect of this enormous field and is destined to become a classic. Ronald L. Graham, Martin Grotschel, and Laszlo Lovasz, three of the world's leading combinatorialists, have compiled a selection of articles that cover combinatorics in graph theory, theoretical computer science, optimization, and convexity theory, plus applications in operations research, electrical engineering, statistical mechanics, chemistry, molecular biology, pure mathematics, and computer science.
ßçûê: Ðóáðèêà: Ìàòåìàòèêà /Àëãåáðà /Êîìáèíàòîðèêà /Ñòàòóñ ïðåäìåòíîãî óêàçàòåëÿ: Ãîòîâ óêàçàòåëü ñ íîìåðàìè ñòðàíèö ed2k: ed2k stats Ãîä èçäàíèÿ: 1995Êîëè÷åñòâî ñòðàíèö: 1120Äîáàâëåíà â êàòàëîã: 10.03.2005Îïåðàöèè: Ïîëîæèòü íà ïîëêó |
Ñêîïèðîâàòü ññûëêó äëÿ ôîðóìà | Ñêîïèðîâàòü ID
Ïðåäìåòíûé óêàçàòåëü
Framework 1914 Francis, R.L. 1898; see “Mirchandani P.B.” Frank, A. 49 120 138 150 154 160 163 164 167 170 218 564 570 572 574 576 577 581 955 1583 1663 1682 Frank, A.A. 578; see “Cunningham W.H.” Frank, A.B. 91; see “Fleischner H.” Frankl theorem 1274 Frankl, P. 376 410—412 418 842 860 1236 1248 1274 1275 1296 1297 1299 1303—1305 1307—1313 1316—1318 1321 1322 1324 1341 1351 1371 1372 1381 1383 1393 1522 1719 1721 1722 1725 1761 1796 Frankl, P.A. 423 1765 1766 1827; N.” Frankl, P.B. 1522 2007 2010; L.” Frankl, P.C. 628 631 635 1303; P.J.” Frankl, P.D. 1325; see “Chung F.R.K.” Frankl, P.E. 1306—1308; see “Deza M.” Frankl, P.F. 1252 1323 1345; P.” Franklin, F. 2173 Franklin, P. 261 2179 Fredman, M. 448 Fredman, M.L. 1144 2020 Free arrangement 2071 2073 Free group 1479 Free matroid 486 494 497 504 Free monoid 1027 1029 Free product 1467 1481 Free subgroup 1753 Freiman, G.A. 986 Freiman’s (doubling) theorem 986 Freivalds, R. 2007 Freud, R. 1013; see “Erdos P.” Freudenthal, H. 1480 Freund, R.M. 1864 Fried, D. 943 Fried, E. 1498 Friedland, S. 17 1209 Friedland, S.A. 1770 1771; N.” Friedman, J. 453 Frieze patterns 2140 Frieze, A. 371 372 1155 Frieze, A.A. 957 1442 1558 1741; M.” Frieze, A.B. 371; see “Fenner T.I.” Frieze, A.M. 72 Frieze, A.M.A. 371; see “Bollobas B.” Fristedt, B. 1123 Frobenius, G. 185 2174 2186 Frucht, R. 1469 1497 Frumkin, M.A. 952 Ftirstenberg, H. 1110 1340 1366 1369 1371 1438—1440 Fuchs. L. 1775 Fueredi, Z. 76 383 387 404 408 409 411 412 416 427 456 457 459 465 818 821 823 1242 1275 1297 1300 1308 1314 1315 1324 Fueredi, Z.A. 862 865 957 1442; I.” Fueredi, Z.B. 829 1314; E.” Fueredi, Z.C. 409; see “Chung F.R.K.” Fueredi, Z.D. 862 1323; P.” Fueredi, Z.E. 1456; see “Erdos Peter Fueredi, Z.G. 412 1297 1309 1310 1321 1322 1324; P.” Fuerer, M. 1513; see “Cai J.” Fuji-Hara, R. 712 Fujishige, S. 572 575 576 578 Fujishige, S.A. 1913; see “Iri M.” Fuju, Y. 763; see “Yamamoto S.” Fulkerson, D.R. 94 141 267 397 401—403 1672 1674 1682 1686 1687 1695 1696 Fulkerson, D.R.A. 1659 1696 1902 2188; G.B.” Fulkerson, D.R.B. 406; see “Edmonds J.” Fulkerson, D.R.C. 185 500 561 1897 2178; J.R.” Fulkerson, D.R.D. 114 125—127 129 133 136 2186 2188; L.R.” Fulkerson, D.R.E. 1545 1661 1903; Jr. Fulkersonian hypergraph 395 402 Fulkerson’s optimum arborescence theorem 1674 Full Ramsey-type theorems 1357 Full time-constructibility 1628 Fully polynomial approximation scheme 1584 1633 Fully space-constructible 1611 Fully submodular function 572 Fully time-constructible function 1609 Fulton, W. 958 1841 Functional digraph 1024 Functional equations 929 1195 1206 Functional gate 2012 Fundamental circuit 554 Fundamental group 1495 1846 2069 Fundamental parallelepiped 923 Fundamental parameters 799 Fundamental theorem of extremal graph theory 1243 Fundamental theorem of projective geometry 655 Furedi theorem 1242 1275 Furrer, F.J. 806 Furst, M. 1625 2013 Furst, M.L. 1486; see “Driscoll J.R.” Furst, M.L.A. 323 1517 Fusion principle 2138 G-set 614 G-space 614 GAB 681; see “Tits geometry” Gabber, O. 1754 1755 Gabow, H. 560 561 566 579 Galambos, J. 1090 Gale diagram 882 893 894 Gale transform 882 Gale, D. 391 894 901 1825 1836 Galil, Z.A. 128 193 1990 1991 Galil, Z.B. 1756; see “Alon N.” Galil, Z.C. 1754 1755; O.” Galiulin, R.V. 923; see “Delone B.N.” Gallai hyperplane 814 Gallai identities 182 Gallai line 812 814 818 Gallai plane 814 815 Gallai theorem 250 254 255 1799 Gallai — Aschbacher decomposition 1476 Gallai — Edmonds structure theorem 202 1471 Gallai — Milgram theorem 44 Gallai — Roy theorem 48 Gallai, T. 43—45 48 82 167 182 199 240 242 250 254—256 263 269 468 1319 1476 Gallai, T.A. 26 39 1263 1274; P.” Gallian, J.A. 65 1473; D.” Galois fields 2181 Galois geometry 657 Galois group 954 Galois theorem 649 Galvin, F. 2113 Gamble, A.B. 215 Game 419 Game theory 628 Gamma function 925 1068 1076 Gammoid 500 Ganelius, T.H. 1125 1126 Gangolli, A. 2136 2158 Gao, Z. 1191 Gao, Z.-C. 1212; see “Bender E.A.” Gao, Z.A. 1202 1203; P.” Gao, Z.C. 59 Garcia-Diaz, A. 125; see “Phillips D.T.” Garcy, M.R. 14 246 247 315 326 910 953 956 1511 1551 1601 1632 1634 1998 1999 Gardiner, A. 1504 1506 1507 Gardner, M. 275 Gardner, M.L. 392 Gardy, D. 1124 1183 1184 Garey, M.R. 1552; see “Cofftnan Jr. Garsia, A.-M. 1856 1858 2059 2060; K.” Garsia, A.M. 1038 1107 2061 Garsia, A.M.A. 1856 2060; A.” Gauss, C.F. 2167 2184 Gaussian coefficient 650 1365 Gehrlein, W.G. 448; see “Fishburn P.C.” Gelatl, C.D. 1559; see “Kirckpatrick S.” Gelatt, C.-D. 1950; see “Kirkpatrick S.” Geller, D.P. 276; see “Chartrand G.” Gelling, E.N. 711 Gel’fand, I.M. 1501 Geman, D. 1997; see “Geman S.” Geman, S. 1997 General linear group 655 Generalized arithmetic progression 986 Generalized assignment problem 1578 1579 1884 Generalized ball 1297 Generalized coloring problem 1624 1625 Generalized Kempe chain 256 Generalized line graph 1734 Generalized m-gon 761 Generalized polygon 674 Generalized polymatroid 581 Generalized quadrangle (GQ) 665 684 Generalized Ramsey number 1347 Generating functions 900 1025 1027 1095 1962 Generator matrix 777 Generator polynomial 784 Generic arrangement 2067 Genericity assumption 1919 Generously transitive 766 Genetics 1985 Genome 1985 Genus of a graph 320 Genus of a group 1493 Genus of a surface 1487 Geometric graph 684 Geometric lattice 496—498 516 1055 1713 1857 Geometric lattice of flats 830 Geometric realization 1843 Geometric simplicial complex 1843 1859 Geometrical dual 2178 Geometry 2180 Geometry of numbers 921—923 929 956 Geramita, A.V. 730 Gerards, A.M.H. 217 1694 Gerards, A.M.H.A. 1692; see “Cook W.” Gerards, B. 531 546 Germa, A. 25 1263; D.” Germa, A.A. 710; see “Bermond J.-C.” Gerver, J.L.; see Ramsey, L.T. 1006 Gessel, I.M. 1110 1155 1209 Getu, S. 1184 1211 Gewirtz graph 701 Ghinelli, D.. see Del Fra, A. 683 Ghouila-Houri, A. 1409 1665 Giancarlo, R. 1990 1991; Z.” Giant component 357 Gielen, M. 1966; see “Brocas J.” Gilbert — Varshamov bound 781 Giles, F.R. 1673 1676 1678 Giles, R. 323 1676 1694 Giles, R.A. 573 574 1672—1674 1678; J.” Gill, J. 1621; see “Baker T.” Gillenson, M.L. 215; see “White L.J.” Gilmore, P.C. 267 Ginibre, J. 447; see “Fortum C.M.” Ginzburg, A. 1769; see “Erdos P.” girth 10 842 1264 1503 1752—1754 1757 1810 Glaisher, J.W.L. 2173 Glas, R. 36; see “Egawa Y.” Glcbskii, YV. 1337 Gleason, A.M. 671 Glover, F. 566; see “Brezovec C.” Glover, H.H. 334 342 2178 Gluing lemma 1848 Go 2119 2129 Goddyn, L.A. 92 296; B.” Goddyn, LA. 92 Godel, K. 1605 Godel’s compactness theorem 2092 Godsil, C.D.A. 1209 1455 1460 1468 1470 1474 1477 1496 1500 1502 1507 1522 1523 1713 1715—1718 1724 1726 1727 1729 1731 1732 Godsil, C.D.B. 73; see “Alspach B.” Godsil, C.D.C. 1460 1500; L.” Goemans, M.X. 1592 Goethals, J.-M. 701 767 768 1507 1734; R.J.” Goethals, J.-M.A. 717 718 752 753 1715 1716 1718; Ph.” Goethals, J.M. 701 716 730 750 753 802 Goidschmidt, D. 1504; see “Delgado A.” Golay codes 716 791 794 Goldbach’s conjecture 971 982 Goldberg conjecture 275 Goldberg, A.V. 114 125 128 135 Goldberg, M.K. 275 Goldberg, M.V. 1582 Golden identity 248 Golden ratio 248 Golden, B. 1885; see “Bodin L.” Goldfarb, D. 1667 Goldman, W.M. 943; see “Fried D.” Goldreich, O. 1511 1515 2028 2032 2035 Goldreich, O.A. 2007; see “Chor B.” Goldreich, O.B. 1486; see “Even S.” Goldschmidt, D.M. 1504 Goldstein, L. 1996 1997 Goldstein, L.A. 1090; see “Arratia R.” Goldwasser, S. 1630 2028 2031 2034 Golender, V.E. 1960 Goljan, M. 313; see “Kratochvil J.” Golumbic, M. 399 Golumbic, M.C. 236 1994 1995 Gomory, R. 130 Gomory, R.E. 207 1672 1691 2188 Gomory-Hu tree 130 Gondran, M. 1545 Gonnet, G.H. 1205 1213 2018 Good, I.J. 1107 Goodey, P.R. 910 Goodman, A. 1520; see “Babai L.” Goodman, A.A. 87 1238; P.” Goodman, A.J. 1501 Goodman, A.J.A. 1449 1501 1519; L.” Goodman, A.W. 1349 Goodman, J.E. 818 830 832 834 857 865 894 1764 1765 Goppa, YD. 667 Gordon, B. 729 1123 Gordon, C.McA. 304; see “Conway J.H.” Gordon, L. 1090 1103 1134; R.” Gordon, M. 1975 Gorenstein complex 1856 Gorenstein, D. 619 1504 Gosper, Jr. R.W. 1075 1210 Gosper’s algorithm 1075 Gosper’s indefinite hypergeometric summation algorithm 1210 Gottlieb, D.H. 1710 Gough, A. 1970; see “Wang T.” Gould, H.W. 1075 Gould, R.J. 28 Goulden, IP. 1023 1088 1098 1107 1213 GQ 665; see “Generalized quadrangle” GR 592; see “Graph realization” Grabner, P. 1194; see “Flajolct P.” Gradient method 1660 Gradshtcyn, I.S. 1075 Graham, R. 1710 1737 1805 Graham, R.A. 1367; see “Erdos P.” Graham, R.L. 72 139 377 662 848 860 999 1004 1006 1071 1073 1090 1131 1132 1212 1333 1338 1344 1346 1349 1359 1361 1364—1366 1369—1371 1373 1389 1464 1546 1633 1759 2093 2185 Graham, R.L., see “Brown, T.C.” 1368 Graham, R.L.A. 376 377 409 1206 1351; F.R.K.” Graham, R.L.B. 970 998 999 1006 1013 1371; P.” Graham, R.L.C. 1341 1372 1381 1383 1393; P.” Graham, R.L.D. 1551; see “Garey M.R.” Graham-Newman problem 820 Graham-Rothschild theorem 1335 Graham’s conjecture 1007 Gram matrix 767 Granas, A. 1862; see “Dugundji J.” Grant, D.D. 1470; see “Little C.H.C.” Granville, A. 1015; see “Alford W.R.” Graovac, A. 1973 Graph 5 500 2177 Graph 751 Graph 269 Graph 263 264
Ðåêëàìà
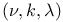
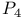isomorphic 
-critical 
|
|
Î ïðîåêòå