Àâòîðèçàöèÿ
Ïîèñê ïî óêàçàòåëÿì
Graham R.L., Grotschel M., Lovasz L. — Handbook of combinatorics (vol. 1)
Îáñóäèòå êíèãó íà íàó÷íîì ôîðóìå Íàøëè îïå÷àòêó?
Íàçâàíèå: Handbook of combinatorics (vol. 1)Àâòîðû: Graham R.L., Grotschel M., Lovasz L.Àííîòàöèÿ: Combinatorics research, the branch of mathematics that deals with the study of discrete, usually finite, structures, covers a wide range of problems not only in mathematics but also in the biological sciences, engineering, and computer science. The Handbook of Combinatorics brings together almost every aspect of this enormous field and is destined to become a classic. Ronald L. Graham, Martin Grotschel, and Laszlo Lovasz, three of the world's leading combinatorialists, have compiled a selection of articles that cover combinatorics in graph theory, theoretical computer science, optimization, and convexity theory, plus applications in operations research, electrical engineering, statistical mechanics, chemistry, molecular biology, pure mathematics, and computer science.
ßçûê: Ðóáðèêà: Ìàòåìàòèêà /Àëãåáðà /Êîìáèíàòîðèêà /Ñòàòóñ ïðåäìåòíîãî óêàçàòåëÿ: Ãîòîâ óêàçàòåëü ñ íîìåðàìè ñòðàíèö ed2k: ed2k stats Ãîä èçäàíèÿ: 1995Êîëè÷åñòâî ñòðàíèö: 1120Äîáàâëåíà â êàòàëîã: 10.03.2005Îïåðàöèè: Ïîëîæèòü íà ïîëêó |
Ñêîïèðîâàòü ññûëêó äëÿ ôîðóìà | Ñêîïèðîâàòü ID
Ïðåäìåòíûé óêàçàòåëü
Spencer, J.H.B. 1210 1212; N.” Spencer, J.H.C. 1347; see “Burr S.A.” Spencer, J.H.D. 72 999 1004 1006 1333 1344 1359 1389 1759 2093 2185; R.L.” Spencer, J.H.F. 410 425; N.” Spencer, J.I. 373 375; E.” Spencer, J.J. 364; see “Shelah S.” Spencer, J.K. 1276 1277 1279; N.” Spencer, J.L. 377; see “Graham R.L.” Sperner family 2186 Sperner poset 444 Sperner theorem 1296 Sperner, E. 444 1270 1296 1862 2186 Sperner’s lemma 444 1862 2186 Sphere 778 880 883 1836 1846 Spherical building 679 Spherical GAB 681 Spieker, B. 2007 Spin glass 1946 1947 1950 Spinster 2139 Spitzer, F. 1744 Split graphs 266 Split off 154 Splitting of vertex 241 Sporadic group 622 Sprague, A. 666 683 Sprague, R.P. 2133 2139 Sprague-Grundy theory 2134 SPREAD 669 Spreads on quadrics 796 Spriggs, J.R. 1913 Sprinrad, J. 590 Sprott, D.A. 730; see “Stanton R.G.” Sprouts 2160 Square design 650 695 Square lattice graph 684 Square of a graph 52 Squashing of a tree 2100 Sreedharan, V. 885 893; B.” Stabiliser 615 Stability molecules 1973 1974 Stability number 40 387 406 422 1591 Stable property 1257 Stable set 40 43 181 225 243 262 387 405 1299 1591 1641 Stable-set polytope 219 269 1591 1667 1687 1693 Stable-set problem 1592 1617 Stacked polytope 899 902 Stahl, S. 321 326 Stallingl, J. 1480 Stallmann, M. 560 561 579; H.” Standard example 456 Standard monomials 2059 Standard normal distribution 366 Standard tableaux 635 2064 Stankevich, I.V. 1975; see “Stankevich M.I.” Stankevich, M.I. 1975 Stanley — Reisner ring 1855 2059 Stanley, R.P. 435 450 895—898 900—902 947 949 1023 1039 1055 1058 1088 1089 1098 1104 1109 1111 1114 1213 1708 1710 1711 1723 1751 1779 1780 1839—1842 1854 1856—1858 1944 2061 2067 2072 Stanley, R.P.A. 1856 2060; A.” Stanton — Cowan numbers 1988 Stanton, D. 765 1023 1048 1053 Stanton, D.A. 839; see “Barniai E.” Stanton, R.G. 715 730 Stanton, R.G.A. 714; see “Billington E.J.” Star 6 386 387 1280 1845 2123 Star body 924 929 934 Star system 1518 Star-shaped 850 Star-triangle transformation 1946 Star-two 2126 Stationary 2114 Stationary distribution 1558 Stationary phase method 1094 Statistical mechanics 1210 Steams, R.E.B. 1549; see “Rosenkrantz D. Stearns, R.E.A. 1628; see “Hartmanis J.” Steckin, B.S. 1275; see Frankl P. Steele, J.M. 1762 Steger, A. 1255; see “Promel H.J.” Steiger, W. 865; see “Pach J.” Steiger, W.L. 991; see “Pinlz J.” Steiglilz, K. 183 1659; C.H.” Stein, P.R. 1992 Stein, S. 864 Stein, S.K. 409 418 1548 Steinberg, L. 893; see “Altshuler A.” Steinberg, R. 236 260 620 Steiner quadruple system 703 1498 Steiner system 499 500 696 751 Steiner triple system (STS) 654 708 1456 1498 1501 1511 2181 Steiner, J. 2181 Steinertree 1563 1564 1571 1573 Steinhaus, H. 2145 Steinitz problem 878 885 Steinitz theorem 310 Steinitz, E. 878 882 885 899 1655 Steinitz-Maclane axiom 485 Steinlein, H. 1864 Steinparz, E. 220; see “Muhlbacher J.” Stellar subdivisions 902 Stellmacher, B. 1504; see “Delgado A.” Stembridge, J.R. 1732 Stepanov, V.E. 354 361 Sterboul, E 220 Stereoisomers 1960 1965 1970 Stevens, W.L. 2182 Stewart, B.M. 1238; see “Nordhaus E.A.” Stewart, C.L. 991; see “GyBry K.” Stewart, C.L.A. 991 Stewart, C.L.B. 991; see “Erdos P.” Stiebitz, M. 242 254 Stiebitz, M.A. 277; see “Fleischner H.” Stiebitz, M.B. 236 255 2167; H.” Stiegler, G J. 2189 Stinson, D.R.A. 711 730 Stinson, D.R.B. 714; see “Billington E.J.” Stinsor, D.R.C. 712; see “Seah E.” Stinton, D.R.D. 711; see “Rees R.” Stirling numbers 1095 1182 Stirling of the first kind 1025 1027 1041 Stirling of the second kind 1041 Stirling’s formula 1067 1076 1091 1173 1179 Stoane, N.J.A.G. 797; see “Hammons Jr.A.R.” Stockmeycr, L.J. 1629 Stockmeyer, L. 246; see “Garey M.R.” Stockmeyer, L.J.A. 1623; see “Chandra A.K.” Stockmeyer, L.J.B. 1625; see “Meyer A.R.” Stockmeyer, P.K. 1521 Stoer, J. 1654 Stoer, M. 1573; see “Grotschel M.” Stohr, A. 987 Stolarsky, KB. 1194 1437 Stone, A.H.; see Erdos, P. 239 836 1243 1244 Stong, R. 89 Stong, R.E. 1844 1854 1857 Straight line program 1519 Straight, H.J. 1281 Straightening syzygies 2062 Strambach, K. 639; see “Barlotti A.” Strange, K.E. 166 Strassen, V. 2016 Strassen, V.A. 1612; see “Solovay R.” Straus, E.G. 705; see “Chowla S.” Straus, E.G.A. 862 865 1371; P.” Straus, E.G.B. 848; see “Graham R.L.” Straus, E.G.C. 863; see “Hales A.W.” Street, A.P. 2182 Street, A.P.A. 712 730 752; W.D.” Street, D.J. 2182; see “Street A.P.” Stresses 900 Strict complete digraph 15 Strict digraph 15 Strict xyz-conjecture 446 String graph 314 Strommer, T.O. 821 822 Stromquist, W.R. 262; see “Alberlson M.O.” Strong (strongly connected) digraph 16 Strong Chvatal rank 1692 Strong circuit axiom 489 493 Strong component 115 Strong component of a digraph 16 Strong connectivity 34 Strong edge connectivity 34 Strong generating set 637 Strong generating set (SGS) 1517 Strong irregularity 1440 Strong map 509 510 Strong perfect graph conjecture 268 Strong product 1464 1466 1736 Strongly 1268 Strongly 1619 Strongly compact 2092 Strongly connected 115 119 Strongly connected complex 1856 Strongly Hamilton-connected digraph 68 Strongly Hamiltonian 80 Strongly inaccessible cardinal 2112 Strongly k-connected 34 Strongly k-edge-connected 34 Strongly polynomial algorithm 135 1583 1584 1663 Strongly reconstructible 1465 Strongly regular graph 684 750 1462 1501 1513 Strongly stable set 387 417 Stroock, D. 1742; see “Diaconis P.” Stroock, D.A. 1559; see “Holley R.” Structural formula 1959 Structural Ramsey theorem 1337 1377 1378 Structure of type 1377 STS see “Steiner triple system” Sturmfels, B. 882 887 890 2059 2063 Sturmfels, B.B. 888 889 894 1822 1843; J.” Sturmftls, B.A. 520 603 1835 1837 1861 2066; A.” Sturtevant, D. 1285 1286 1823 1853; J.” Subadditive ergodic theorem 1997 Subadditive function 1937 Subadditive stochastic processes 1937 Subcartesian product 615 Subcritical phases 360 Subdirect product 1460 Subdivision 17 256 1859 Subgraph bipartite 1696 Subgraph bridge of 40 Subgraph chord of 40 Subgraph color-critical 254 Subgraph Eulcrian 1581 Subgraph excluded 1475 Subgraph forbidden 1268 2178 Subgraph induced 8 Subgraph induced forbidden 1254 Subgraph spanning 7 Subgraph unicychc 1550 Subgroup 1966 Subgroup lattice 1857 Subhypergraph 386 397 Sublattice 924 954 Submatroid 494 Submoduiar flow algorithm 575 577 Submodular Amction 485 501 502 510 521 566 1676 Submodular flows 573 Submodular junction minimization 568 Submodular polyhedra 571 Submodularity 497 Subscheme 766 Subset sums 991 Subset-sum problem 954 1562 1585 1618 1633 2030 Subsets ordered by inclusion 459 subspace 484 696 Subspace lattice 1501 Substituents 1965 Substituttonal isomers 1964 Subsynthons 1969 Subtraction 1043 1049 Subtraction games 2135 Subtraction of singularities 1153 Subtree disjointness problem 2011 Successive minimum 925 926 Successive with respect to 925 Successor cardinal 2112 Successor ordinal 2110 Succinct certificate 14 Sudan, M. 1592; see “Karger D.” Sugihara, K. 1913 1919—1922 Sum of games 2124 Sum sets 983 991 Summation by parts 1078 Summation function 2014 Sumner, D.P. 1280 Sumner, D.P.A. 66; see “Oberly D.J.” Sumner. D. 62 66; M.” Sums of circuits 92 547 Sunflower 1296 1456 Sunflower theorem 2016 Sup-norm short vector problem 953 Superconcentrators 1754 1755 1758 Supercritical phases 360 Supermatroid 520 521 Supermodular function 570 Supersolvable 2067 Suppes, P. 460; see “Scott D.” Support of a vector 603 Supporting hyperplane 1655 Suranyi, J. 266; see “Hajnal A.” surface 1487—1489 1491 1493 Suspense 2149 2151 Suspension 1844 Sutherland, J.W. 836 Sutyok, M. 1418; see “Komlos J.” Suzuki — Tits ovoid 659 661 Svenonius, L. 640 Svrakic, N.M. 1105 1160; V.” Swart, G. 881 Swart, H. 80; see “Entringer R.C.” Swiercz, S. 672 673 683; C.W.” Swiercz, S.A. 701 2183; C.W.H.” Swierczkowski, S. 1440 Swift, J.D. 704; see “Hall Jr.M. Swinnerton-Dyer, H.P.F. 933 958 Switching class 1499 Sykes, M.F. 1936 Sylow subgroup 639 Sylvcster-Gallai theorem 812 813 1837 Sylvester, JJ. 812 823 1959 2173 2177 Sylvester’s problem 812 817 Symmetric convex body 924 926 930 931 935 937 Symmetric design (SBIBD) 695 698 1511 Symmetric exchange axiom 579 Symmetric function 1056 2168 Symmetric greedy algorithm 580 Symmetric group 2053 Symmetry codes 794 Symmetry permutations 1966 Symmetry point group 1965 Symplectic group 620 Symplectic polar space 663 SYNCHEM 1969 1970 Syndrome 777 SYNLMA 1970 Synthon 1969 Synthon stability 1969 System of distinct representatives (SDR) 185 System of imprimitivity 616
Ðåêëàìà
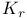-saturaled 
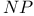-complete 
|
|
Î ïðîåêòå