Expansion of 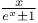 , , 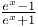 1539 1543—1544 1539 1543—1544
Expansion of 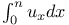 in terms of in terms of  3778 3778
Expansion of 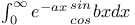 and summation of the series J.41 and summation of the series J.41
Expansion of 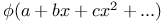 (Arbogast) 1536 CD.1 6 (Arbogast) 1536 CD.1 6
Expansion of 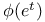 (Herschel) 3757 (Herschel) 3757
Expansion of  2931—2932 2945 2960—2962 Me.78 2931—2932 2945 2960—2962 Me.78
Expansion of  , powers of , powers of  Me.78 Me.78
Expansion of  , powers of , powers of 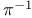 Me.83 Me.83
Expansion of  , powers of , powers of 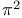 858 858
Expansion of 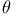 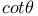 in powers of in powers of 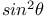 Q.6 Q.6
Expansion of 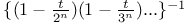 J.40 J.40
Expansion of 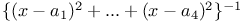 C.95 C.95
Expansion of 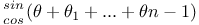 A.34 A.34
Expansion of 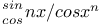 A.4 A.4
Expansion of a function of 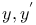 in ascending powers of in ascending powers of 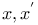 when when 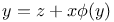 and and 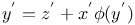 as in 1552 J.48 as in 1552 J.48
Expansion of a function of a complex variable M.19
Expansion of a function of a function AJ.2 3
Expansion of a function of a rational fraction At.65
Expansion of a function of n variables C.60 J.66
Expansion of a polynomial 137 Z.26
Expansion of a quartic function A.35
Expansion of alg. functions C.89 Z.45
Expansion of alg. functions, Eisenstein's th J.45
Expansion of an arc in linear functions of sines or tangents of fractions of the arc in g.p L.43
Expansion of Bernoulli's numbers 1545
Expansion of circular functions J.24 Q.5
Expansion of cosec x 2914 2918
Expansion of cot x 2911 2916 C.88 Q.17
Expansion of differential coefficients by f.d.c and the converse J.16
Expansion of do. when 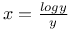 1570 1570
Expansion of elliptic functions A.19
Expansion of elliptic functions and of their powers C.83
Expansion of elliptic functions and of their powers, cos amx L.64
Expansion of equations L.50
Expansion of exponential functions N.82
Expansion of f(0) (Bernoulli) 1510
Expansion of f(x) (Maclaurin) 1507 3759
Expansion of f(x+h) 1500—1509 1520 see
Expansion of f(x+h), Abel's th 1572
Expansion of f(x+h), Boole 1547 AJ.3
Expansion of f(x+h), Stirling 1546
Expansion of f(x+h, y+k) 1512 1521
Expansion of f(x, y) 1516 1523 Me.3
Expansion of f(y) in powers of 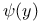 (Burmann) 1559 (Burmann) 1559
Expansion of fractions 248
Expansion of functions of infinitesimals G.12
Expansion of functions, 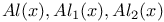 (Weierstrass's functions) in powers of the modulus C.82 85 86 L.79 (Weierstrass's functions) in powers of the modulus C.82 85 86 L.79
Expansion of higher integrals of log x A.4
Expansion of holomorphic functions M.21
Expansion of holomorphic functions by arcs of circles C.94
Expansion of implicit functions 551 1550 L.81
Expansion of integrals A.1
Expansion of integrals of linear d.e An.71
Expansion of integrals of log x A.4
Expansion of log y and 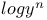 in powers of in powers of 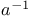 when when 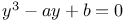 1553—1554 1553—1554
Expansion of logarithms 152—159 N.82
Expansion of n, alg. functions from n eqs G.11
Expansion of nth derivative of  A.4 A.4
Expansion of numbers M.21
Expansion of powers of arc in powers of sines J.11
Expansion of sec x 1526 A.16 C.88 J.26
Expansion of sin 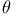 and cos and cos 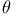 in powers of in powers of 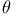 764 1531 A.5 29 C.16 764 1531 A.5 29 C.16
Expansion of tan x 1525 2913 2917 A.16 C.88 N.57
Expansion of xexp.[xexp.[xexp, &c. J.28
Expansion of y in powers of x when 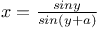 796 1558 796 1558
Expansions of a function in a series A.31 An.7 thsAJ.3 4 C.7 13 17 20 CM.4 J.90 L.38 46 76 M.16 Mel.3 Mem.33 N.82 83 see "Summation"
Expansions of a function in a series by a series C.93 95
Expansions of a function in a series by Bessel's function J.67 M.10 17 Z.1
Expansions of a function in a series by binomial theorem 125
Expansions of a function in a series by factorials 3730
Expansions of a function in a series by generating functions 3732
Expansions of a function in a series by indeterminate coefficients 232 1527—1534 A.3
Expansions of a function in a series by logarithmic method C.9
Expansions of a function in a series by Maclaurin's th 1524
Expansions of a function in a series of another function 1559 C.95 96
Expansions of a function in a series of circular functions 2955 A.11 CM.3 J.43 L.36 Q.12
Expansions of a function in a series of circular functions of imag. arcs J.6
Expansions of a function in a series of denominators of convergents C.46 JP.21
Expansions of a function in a series of explicit functions 1500—1547
Expansions of a function in a series of exponentials J.80
Expansions of a function in a series of faculties of the variables Mem.31
Expansions of a function in a series of implicit functions 1550—1573
Expansions of a function in a series of Jacobian functions An.82
Expansions of a function in a series of Legendre's functions, 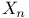 An.75 An.75
Expansions of a function in a series of periodic quantities C.52 53 JP.11
Expansions of a function in a series of powers of a polynomial C.86 J.53 88
Expansions of a function in a series of powers of another function Mem.33 N.74
Expansions of a function in a series of powers of the variable At.57 C.19 L.46
Expansions of a function in a series with limits C.34
Expansions of a function in a series within a given interval according to the mean values of the function and of its successive derivatives in this interval C.90
Expansions of a function in a series, coefficients of, gn form C.85
Expansions of a function in a series, coefficients of, gn form, gn property J.41
Expansions of a function in a series, connected with a 2nd order d.e C.5 L.36 37
Expansions of a function in a series, extended class of C.82
Expansions of a function in a series, extended class of, approximating to functions of very large numbers L.78
Expansions of a function in a series, num Q.3 Z.2
Exponentia1, th, functions P.16
Exponentia1, th, replaced by an infinite product C.99
Exponential, th 149 N.52
Exponentials, successive of Euler L.45
Exponents N.57 P.1776
Exponents, reduction for d.i C.16
Factorials, 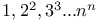 Me.78 Me.78
Factorials, 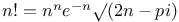 (Stirling) Q.15 (Stirling) Q.15
Factorials, 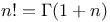 2290 2290
Factorials, 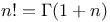 , approx. to when n is large C.9 50 J.25 27 L.39 , approx. to when n is large C.9 50 J.25 27 L.39
Factorials, 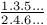 theorem 339 theorem 339
Factorials, 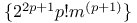 CM.3 CM.3
Factorials, C(n, r) when  J.43 J.43
Factorials, calculus of L.57 N.60 Pr.22 Q.12 Q.f8
Factorials, geom. i.e  C.17 C.17
Factorials, notation 94 2451 Q.2
Factorials, reciprocal C.17
Factorials, treatment by limits J.39
Factors 1—27
Factors in analysis of integral functions M.15
Factors of  thQ.15 16 thQ.15 16
Factors of  , th of Lagrange AJ.3 , th of Lagrange AJ.3
Factors of 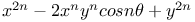 807 807
Factors of 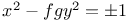 A.33 A.33
Factors of 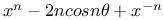 CP.11 Me.76 CP.11 Me.76
Factors of an equation 400 J.3
Factors of an equation, condition for a factor of the form  A.55 63 A.55 63
Factors of composite numbers 274 J.11
Factors of polynomials and geo.ap J.29 89
Factors, 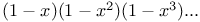 C.96 C.96
Factors, application to rotations to indicate direction J.28
Factors, complex C.24
Factors, equal, of integral polynomials C.42 L.56
Factors, irreducible, of an integral function according to a prime modulus p C.86
Factors, linear, resolution into N.82
Factors, of 100...01 Me.79
Factors, product of an infinite number of A.59
Factors, product of an infinite number of, 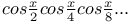 N.70 N.70
Factors, radical, of numbers C.24 25
Factors, tables of (Burchardt's) p.7 to 4100 J.46
Factors, tables of (Burchardt's) p.7, geo. properties J.22
Factors, transformation of A.57
Faculties, analytical J.7 11 33 35 40 44 51
Faculties, analytical, coefficients of A.9 11 At.75
Faculties, analytical, divisibility of A.48
Faculties, analytical, numerical, of 2nd order Mem.38
Faculties, analytical, series Z.4
Fagnani's theorem 6088 A.26 LM.5 13 23 Z.1
Fagnani's theorem, curves having Fagnanian arcs LM.11
Fagnani's theorem, stereometric analogy Z.17
Faisceaux of binary forms having the same Jacobian C.93
Faisceaux of circles C.76
Faisceaux of conics Z.20
Faisceaux of lines and surfaces N.53 83
| Faisceaux of tortuous cubics in connection with ray-complexes Z.19
Faisceaux, curvature relations Z.15
Faisceaux, formation of C.45 CM.3
Faisceaux, intersections of N.72
Faisceaux, intersections of, degree of the resulting curve J.71
Faisceaux, plane N.53
Faisceaux, plane, defined by a first order d.e C.86
Fan of Sylvester E.33
Faure's theorems Gr.1 19
Faure's theorems and Painvin's N.61
Fermat's theorems of  369 A.32 AJ.3 J.8 369 A.32 AJ.3 J.8
Fermat's theorems of 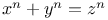 being insoluble when n is an odd prime, &c An.57 C.gz84 96 91 J.40 87 TE.21 being insoluble when n is an odd prime, &c An.57 C.gz84 96 91 J.40 87 TE.21
Fermat's theorems of 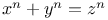 , , 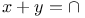 , , 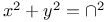 Mem.26 Mem.26
Fermat's theorems of 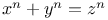 , analogous theorem J.3 , analogous theorem J.3
Fermat's theorems of 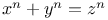 , and periodic functions Me.76 , and periodic functions Me.76
Fermat's theorems of 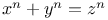 , case of n=14 J.9 , case of n=14 J.9
Fermat's theorems of the semicircle A.27 30 31 gzA.31
Fermat's theorems of the semicircle, method of maxima C.50
Feuerbach's, th of the circle A.59
Feuerbach's, th of the triangle Me.84
Fifteen girl problem E.34 35 Q.8 9
Figurate numbers 289 A.5 69
Finite difference equations AJ.4 An.59 CD.2 CM.1 3 4 CP.6 JP.6 L.83 P.60 Pr.10
Finite difference equations of integrable form C.54
Finite difference equations of mixed differences Q.10
Finite difference equations of the kind 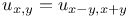 CM.4 CM.4
Finite difference equations, linear AJ.7 An.50 At.65 Q.1
Finite difference equations, linear, determination of arbitrary constants A.27 At.65 G.7
Finite difference equations, linear, first order, constant coefficients C.8
Finite difference equations, linear, integration to differences of any order J.12
Finite difference equations, linear, with variable coefficients C.17
Finite difference equations, partial, constant coefficients C.8
Finite difference equations, partial, linear of 2nd order C.98
Finite difference equations, partial, of physics C.73
Finite differences of functions of zero TI.17
Finite differences of powers converted into d.i JP.17
Finite differences, calculus of 3701—3830 A.13 18 24 63 C.70 J.11 12 13 14 15 16 Me.82 Mel.5 Mem.13 N.69 thsP.16 17
Finite differences, calculus of  Ac.5 Ac.5
Finite differences, calculus of  , in a function of , in a function of  N.61 N.61
Finite differences, calculus of 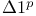 and Bernoulli's numbers An.59 and Bernoulli's numbers An.59
Finite differences, calculus of 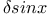 and and 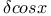 CM.1 CM.1
Finite differences, calculus of 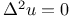 An.73 An.73
Finite differences, calculus of 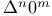 3744 Q.5 8 9 3744 Q.5 8 9
Finite differences, calculus of 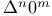 , Herschel's table N.54 , Herschel's table N.54
Finite differences, calculus of 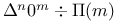 table of CP.13 table of CP.13
Finite differences, calculus of 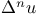 in successive derivatives of u 3761 N.73 in successive derivatives of u 3761 N.73
Finite differences, calculus of first and nth differences 3706
Finite differences, calculus of, ap. to complex variability An.82
Finite differences, calculus of, ap. to complex variability, ap. to i.eq An.50
Finite differences, exercises No.44 47
Finite differences, formulae CD.9 Q.2
Finite differences, formulae, sum and difference J.58
Finite differences, H(n, r) value of Q.9
Finite differences, integrals C.39 57 JP.4 L.44
Finite differences, integrals, 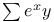 A.6 No.44 A.6 No.44
Finite differences, integrals, expressed by definite integrals An.53
Finite differences, inverse method C.74 P.7
Finite differences, involving ![$\sqrt[7]1$](/math_tex/464e782a4697c5049f1b51c4b0d5874f82.gif) Me.78 Me.78
Fleflecnodal planes of a surface Q.15
Flexure AJ.2 Me.2
Flexure of ruled surfaces An.65
Flexure of spaces LM.9
Flexure of spherical surfaces Me.77
Fluctuating functions 2955a LM.5 M.20 TI.19
Fluents P.1786
Fluents of irrational functions P.16
Focal properties of a parabola 1220 1223—1226 1230—1224 4231 4235—4238 G.22
Focal properties of a quadric surface An.59 N.58
Focal properties of conics 1163 1167—1169 1181 1286—1288 4298—4306 4336—4345 4378 4382 4516 4550—4558 4719—4721 5008—5016 CD.7
Focal properties of curves CD.7
Focal properties of homographic figures N.71
Focal quadrics of a cyclide Me.85
Focal, chords of conics 1226 4235 4339
Focal, circle of conics Mel.2
Focal, distances 4298 N.64
Focal, pedal of a conic N.66
foci J.64 N.42 44 53 85 Q.2 a.c
Foci of cones N.79
Foci of conics 1160 trA.25 63 64 cn69 gzC.22 L.39 CP.3 N.69 74 78 81 82 t.cQ.8 13 12 45
Foci of conics of four tangents 5029 N.83
Foci of conics through four points N.83
Foci of conics, analogous points in higher plane curves J.10
Foci of conics, coordinates of 4516
Foci of conics, eq. of LM.11 o.cE.40
Foci of conics, exterior N.79
Foci of conics, gen.eq N.48
Foci of conics, locus, a cubic M.5
Foci of conics, negative A.64
Foci of conics, to find them Q.25
Foci of conics, to find them, from gn.eq 5008
Foci of conics, under three conditions Q.8
Foci of curves C.82
Foci of curves, nth class 86 N.59 79
Foci of differential curve of a parabola A.58
Foci of in conic of an n-tic, locus of E.21
Foci of lines of curvature of an ellipsoid Z.26
Foci of quadrics N.42 66 74 75 78
Foci of quartics J.56
Foci of surfaces C.74
Foci of surfaces of revolution N.74
Foci of the section of a quadric by a plane N.64 70
Foci of the section of a quadric by another quadric N.47
Folium of Descartes 5360 N.44
Forms, theory of M.18
Forms, theory of higher degree Mo.83 Pr.38
Forms, theory of reciprocity principle An.56
Formula G.15 19
Formulae for log 2, &c. Me.79
Formulae in the Fund.Nova Me.76
Formulae of reduction in i.c 1965 Me.3
Four colors problem AJ.2
Four right lines not 2 and 2 in same plane J.5
Four-point problem E.5 6 8
Fourier — Bessel function J.69 M.3
Fourier's formula in i.c 2726—2742 CM.3 J.36 69 L.36 M.4 Me.73 Q.8 gzZ.9
Fourier's formula in i.c, ap.to calculation of differentials J.13
Fourier's theorem 518 528 An.50 75 J.13 M.19 Me.77 82 83
Fourier's theorem, ap. to a function of a complex variable M.21
Fractions AJ.3 G.9 pr16 J.88 L.10
Fractions, continued, decimal, partial, vanishing, &c. AJ.3 G.9 pr16 J.88 L.10
Fractions, number expressible by 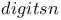 C.96 C.96
Fractions, reduction to decimals A.1 25
Fractions, transformation into decimals A.11
Frullani's formula 2700 LM.9
Fuchs's theorem on 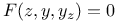 C.99 C.99
Fuchsian functions C.92 93 94 95 96
Functional equations CM.3 J.90 TE.14
Functional equations, 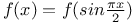 C.88 C.88
Functional equations, 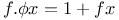 C.99 C.99
Functional equations, 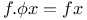 C.88 C.88
Functional equations,  J.5 J.5
Functional equations, 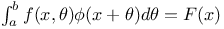 , to find , to find 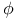 Pr.8 Pr.8
Functional equations, 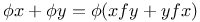 J.2 J.2
Functional equations, 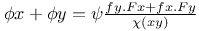 J.46 J.46
Functional equations, 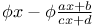 Q.15 Q.15
Functional equations, 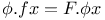 , to find , to find 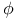 Mem.31 Mem.31
Functional images in ellipses Q.17
Functional images in ellipses in Cartesian ovals Q.18
Functional powers Mem.38
Functional powers, symbols Q.4
Functions from functional equations M.24
Functions from Gauss's equation C.92
Functions of 4 and 5 letters L.56
Functions of 4, 5, and 6 letters L.50
Functions of 6 variables which take only 6 different values through their permutation, not including 5 symmetrical permutations A.68
Functions of 7 letters C.57 95
Functions of a circular area from a given integral condition Z.26
Functions of a real variable, connexion with their derivation M.23 24
Functions of a variable analogous to the polynomials of Legendre C.95
Functions of an analytical point, ths C.95
|
 |
|
О проекте
|
|
О проекте



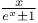 ,
, 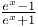
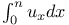 in terms of
in terms of 
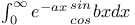 and summation of the series
and summation of the series 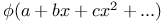 (Arbogast)
(Arbogast) 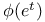 (Herschel)
(Herschel) 
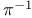
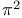
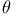
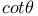 in powers of
in powers of 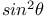
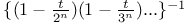
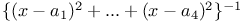
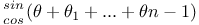
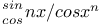
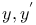 in ascending powers of
in ascending powers of 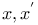 when
when 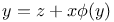 and
and 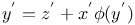 as in 1552
as in 1552 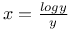
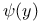 (Burmann)
(Burmann) 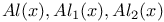 (Weierstrass's functions) in powers of the modulus
(Weierstrass's functions) in powers of the modulus 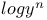 in powers of
in powers of 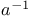 when
when 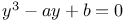

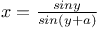
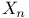
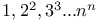
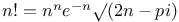 (Stirling)
(Stirling) 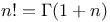
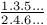 theorem
theorem 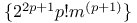
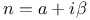
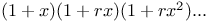
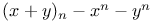
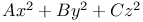 , th of Lagrange
, th of Lagrange 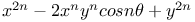
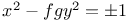
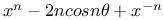

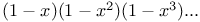
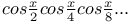

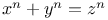 being insoluble when n is an odd prime, &c
being insoluble when n is an odd prime, &c 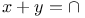 ,
, 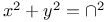
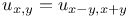

 , in a function of
, in a function of 
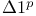 and Bernoulli's numbers
and Bernoulli's numbers 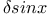 and
and 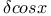
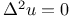
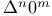
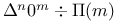 table of
table of 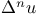 in successive derivatives of u
in successive derivatives of u 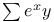
![$\sqrt[7]1$](/math_tex/464e782a4697c5049f1b51c4b0d5874f82.gif)
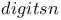
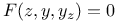
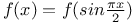
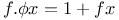
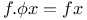

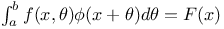 , to find
, to find 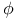
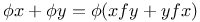
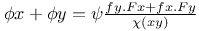
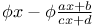
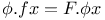 , to find
, to find