Differential coefficients or differential quotients or derivatives, successive or of nth order, 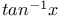 1468 apN.9 1468 apN.9
Differential coefficients or differential quotients or derivatives, successive or of nth order, 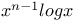 1466 1466
Differential coefficients or differential quotients or derivatives, successive or of nth order, 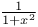 1469 1469
Differential coefficients or differential quotients or derivatives, successive or of nth order, 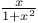 1470 J.8 1470 J.8
Differential coefficients or differential quotients or derivatives, successive or of nth order,  A.3 A.3
Differential coefficients or differential quotients or derivatives, successive or of nth order, 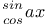 1461 N.62 1461 N.62
Differential coefficients or differential quotients or derivatives, successive or of nth order, 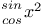 2862 2862
Differential coefficients or differential quotients or derivatives, successive or of nth order, and summation symbols J.33 ths32
Differential coefficients or differential quotients or derivatives, successive or of nth order, independent repres. of M.4
Differential coefficients or differential quotients or derivatives, successive or of nth order, of 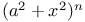 2860 2860
Differential coefficients or differential quotients or derivatives, successive or of nth order, of 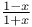 1467 1467
Differential coefficients or differential quotients or derivatives, successive or of nth order, of a function of a function G.13
Differential coefficients or differential quotients or derivatives, successive or of nth order, of a function of a function, n = 4 1419
Differential coefficients or differential quotients or derivatives, successive or of nth order, of a logarithmic function A.8
Differential coefficients or differential quotients or derivatives, successive or of nth order, of a product 1460 1472
Differential coefficients or differential quotients or derivatives, successive or of nth order, of a sum, product, or quotient 1411
Differential coefficients or differential quotients or derivatives, successive or of nth order, of functions of several variables C.93
Differential coefficients or differential quotients or derivatives, successive or of nth order, tan x A.12
Differential equations (D.E.) p.460 3150—3637 A.1 52 67 AJ.4 An.50 C.8 15 23 29 42 54 70 83 CM.3 E.9 J.1 36 58 64 66 74 75 76 78 86 91 L.38 52 56 LM.4 10 M.8 12 25 Man.79 Me.81 Mem.30 Mo.84 N.72 80 Pr.7 TI.13 Z.4 16 27
Differential equations and elliptic functions L.49
Differential equations and p.d.e of first order J.23
Differential equations and tortuous curves L.53
Differential equations for a conical pendulum A.84
Differential equations for roots of algebraic equations P.64 Pr.13
Differential equations in linear geometry M.5
Differential equations in problem of n bodies An.83
Differential equations of a conic E.38
Differential equations of a surface G.2
Differential equations of astronomy C.9 29 P.4
Differential equations of curves having the same polar surface An.76
Differential equations of dynamics C.5 26 40 CD.2 G.1 4 L.37 49 52 55 72 74 M.2 17 25 Mel.4 Pr.12 P.54 55 63
Differential equations of families of surfaces Me.77
Differential equations of first order 3221—3236 A.29 C.40 45 66 M.3
Differential equations of first order, 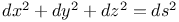 L.48 L.48
Differential equations of first order, 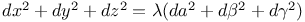 L.50 L.50
Differential equations of first order, 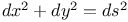 and analogous eqs L.73 and analogous eqs L.73
Differential equations of first order, 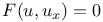 C.93 C.93
Differential equations of first order, 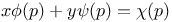 3226 3226
Differential equations of first order, adx+bdy=ds 3287
Differential equations of first order, Clairaut's equation, y=px+f(p) 3230 CM.3 Me.77
Differential equations of first order, homogeneous in x and y 3234
Differential equations of first order, integration by second order d.e A.46
Differential equations of first order, linear p467 C.86 G.13 algG.18 M.23
Differential equations of first order, linear, 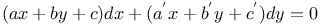 3205 p471 L.59 3205 p471 L.59
Differential equations of first order, linear, 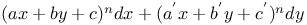 A.64 A.64
Differential equations of first order, linear, 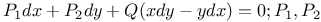 being homogeneous and of the pth deg. in x, y; Q homogeneous and of the qth deg. 3212 being homogeneous and of the pth deg. in x, y; Q homogeneous and of the qth deg. 3212
Differential equations of first order, linear, 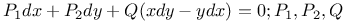 different linear functions of x, y C.78 83 L.45 J.24 different linear functions of x, y C.78 83 L.45 J.24
Differential equations of first order, linear, 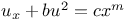 (Riccati's eq.) 3214 A.40 C.11 85 ext28 JP.14 L.41 P.81 Q.7 11 16 (Riccati's eq.) 3214 A.40 C.11 85 ext28 JP.14 L.41 P.81 Q.7 11 16
Differential equations of first order, linear, 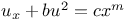 (Riccati's eq.), m=-6 E.7 (Riccati's eq.), m=-6 E.7
Differential equations of first order, linear, 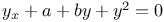 J.25 J.25
Differential equations of first order, linear, 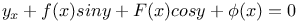 L.46 L.46
Differential equations of first order, linear, 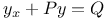 , where P, Q involve x only 3210 , where P, Q involve x only 3210
Differential equations of first order, linear, 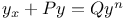 3211 3211
Differential equations of first order, linear, 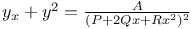 , where P, Q, R are functions of x Mem.11 , where P, Q, R are functions of x Mem.11
Differential equations of first order, linear, 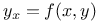 An.73 L.55 An.73 L.55
Differential equations of first order, linear, 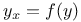 J.9 J.9
Differential equations of first order, linear, 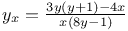 C.88 C.88
Differential equations of first order, linear, 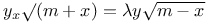 A.42 A.42
Differential equations of first order, linear, 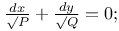 P, Q being quartics in x, y C.66 LM.8 ME.79 P, Q being quartics in x, y C.66 LM.8 ME.79
Differential equations of first order, linear, 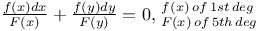 C.92 C.92
Differential equations of first order, linear, allied eqs L.51 Me.78 Q.12
Differential equations of first order, linear, exact 3187
Differential equations of first order, linear, homogeneous 3186
Differential equations of first order, linear, integration by a particular integral C.86
Differential equations of first order, linear, Mdx+Ndy=0 3184 N.74 77
Differential equations of first order, linear, reduction to a continued fraction of a fraction which satisfies a C.98
Differential equations of first order, linear, separation of variables 3185 CM.1
Differential equations of first order, linear, sol. by continued fractions Mem.18
Differential equations of first order, linear, sol. by definite integrals J.12
Differential equations of first order, linear, transformation of Me.83
Differential equations of first order, linear, yy+Py+Q Mem.11
Differential equations of first order, reduction to a linear form with respect to the derivatives of an unknown function C.87
Differential equations of first order, related transcendents Ac.3
Differential equations of first order, separation of variables CD.9
Differential equations of first order, singular solution 3230 A.56 58 CP.9 J.48 Me.73 77
Differential equations of first order, solution by differentiation 3236
Differential equations of first order, solution by factors 3222
Differential equations of first order, transf. by elliptic coords J.65
Differential equations of first order, two variables An.76 J.40 Mem.62 N.50
Differential equations of first order, two variables, singular solution J.38
Differential equations of first order, verified by a reciprocal relation between two systems of values of variables C.15
Differential equations of functions of elliptic cylinders M.22
Differential equations of higher order 3251—3269
Differential equations of higher order, 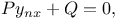 where P, Q are functions of x, y, and the first n-1 derivatives of y J.31 where P, Q are functions of x, y, and the first n-1 derivatives of y J.31
Differential equations of higher order, 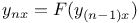 3258 3258
Differential equations of higher order, 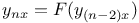 3260 3260
Differential equations of higher order, linear 3237—3250 A.65 C.97 J.16 M.4 Q.18
Differential equations of higher order, linear, 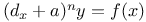 CM.4 CM.4
Differential equations of higher order, linear, 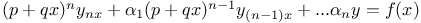 3250 3250
Differential equations of higher order, linear, 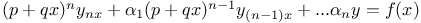 , with p=0 C.96 , with p=0 C.96
Differential equations of higher order, linear, 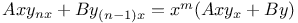 Z.8 Z.8
Differential equations of higher order, linear, 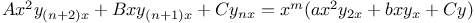 A.38 A.38
Differential equations of higher order, linear, 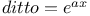 3528 3528
Differential equations of higher order, linear, 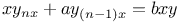 J.2 Z.10 J.2 Z.10
Differential equations of higher order, linear, 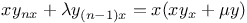 A.86 A.86
Differential equations of higher order, linear, 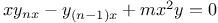 A.40 A.40
Differential equations of higher order, linear, 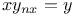 A.26 A.26
Differential equations of higher order, linear, 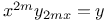 A.42 A.42
Differential equations of higher order, linear, 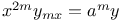 A.32 A.32
Differential equations of higher order, linear, 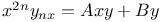 A.33 A.33
Differential equations of higher order, linear, 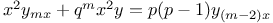 J.2 J.2
Differential equations of higher order, linear, 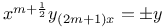 by Bessel's function M.2 by Bessel's function M.2
Differential equations of higher order, linear, 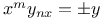 by definite integrals C.48 49 J.57 by definite integrals C.48 49 J.57
Differential equations of higher order, linear, 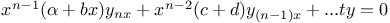 J.39 J.39
Differential equations of higher order, linear, 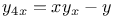 A.1 A.1
Differential equations of higher order, linear, 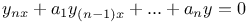 3239 A.40 3239 A.40
Differential equations of higher order, linear, 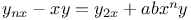 by definite integrals J.17 by definite integrals J.17
Differential equations of higher order, linear, 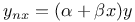 J.10 J.10
Differential equations of higher order, linear, 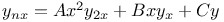 A.53 M.3 A.53 M.3
Differential equations of higher order, linear, 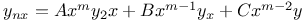 A.29 30 33 38 A.29 30 33 38
Differential equations of higher order, linear, 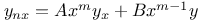 A.28 38 A.28 38
Differential equations of higher order, linear, 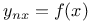 3256 3256
Differential equations of higher order, linear, 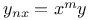 L.39 L.39
Differential equations of higher order, linear, 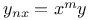 by definite integrals J.19 by definite integrals J.19
Differential equations of higher order, linear, 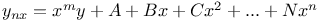 Z.10 Z.10
Differential equations of higher order, linear, 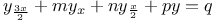 L.44 L.44
Differential equations of higher order, linear, 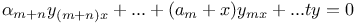 A.47 A.47
Differential equations of higher order, linear, ditto = f(x) 3243 3516
Differential equations of higher order, linear, ditto = f(x), 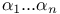 functions of x 3237 J.39 functions of x 3237 J.39
Differential equations of higher order, linear, ditto = f(x), n fractional and all lower orders integral L.36
Differential equations of higher order, linear, ditto=sin mx 3529
Differential equations of higher order, linear, of orders p and m+p, th C.43
Differential equations of hypergeometrical series J.56 57 73
Differential equations of Lame J.89
Differential equations of light M.1
Differential equations of motion C.55
Differential equations of motion of a point C.26
Differential equations of motion of elastic solids Q.13
Differential equations of motion of fluids CP.7
Differential equations of perturbation theory Mem.83
Differential equations of second order Ac.1 An.79 JP.29 C.67 69 80 91 J.90 L.39 LM.11 12 13 16 Z.15
Differential equations of second order by Challis's method, and application to Calc. of Variations A.65 66
Differential equations of second order by factors C.68
Differential equations of second order in the neighbourhood of critical points C.87
Differential equations of second order with algebraic integrals C.82
Differential equations of second order with elliptic function coefficients Ac.3
Differential equations of second order, 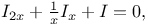 where I is Bessel's function J.56 where I is Bessel's function J.56
Differential equations of second order, 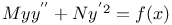 N.79 N.79
Differential equations of second order, 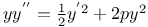 L.73 L.73
Differential equations of second order, 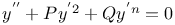 3279 3279
Differential equations of second order, 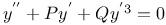 P, Q functions of x 3276 P, Q functions of x 3276
Differential equations of second order, 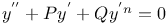 3278 3278
Differential equations of second order, 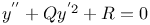 3277 3277
Differential equations of second order, derived from linear eq Me.73
Differential equations of second order, linear A.29 32 55 64 An.63 79 82 C.82 90 91 93 97 J.51 74 L.36 Me.1 M.11 Mo.64 Z.5
Differential equations of second order, linear, 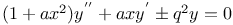 3283 3594 3283 3594
Differential equations of second order, linear, 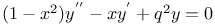 3282 3282
Differential equations of second order, linear,  CM.3 CM.3
Differential equations of second order, linear, 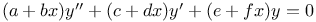 A.58 A.58
Differential equations of second order, linear, 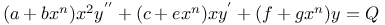 (Pfaff) 3598 J.2 54 (Pfaff) 3598 J.2 54
| Differential equations of second order, linear, 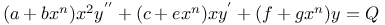 (Pfaff) and like eqs. Z.2 3 (Pfaff) and like eqs. Z.2 3
Differential equations of second order, linear, 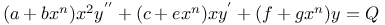 (Pfaff) and like eqs. with b=0 A.38 (Pfaff) and like eqs. with b=0 A.38
Differential equations of second order, linear, 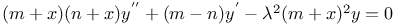 A.42 A.42
Differential equations of second order, linear, 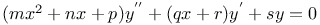 JP.13 Z.4 JP.13 Z.4
Differential equations of second order, linear, 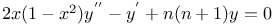 Q.18 Q.18
Differential equations of second order, linear, 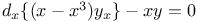 L.54 L.54
Differential equations of second order, linear, 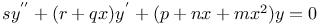 A.23 Z.8 9 A.23 Z.8 9
Differential equations of second order, linear, $x(1-x)y^{''}+(\frac{2}{3}-\frac{7}{6}x)y^{'}+\frac{1}{48}y=0 $Me.82 Q.17
Differential equations of second order, linear, 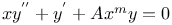 C.39 C.39
Differential equations of second order, linear, 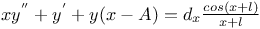 Me.82 Me.82
Differential equations of second order, linear, 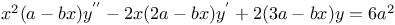 A.28 30 A.28 30
Differential equations of second order, linear, 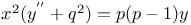 CM.2 CM.2
Differential equations of second order, linear, 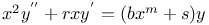 An.51 CD.5 An.51 CD.5
Differential equations of second order, linear, 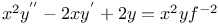 A.28 30 A.28 30
Differential equations of second order, linear, 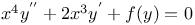 A.28 30 A.28 30
Differential equations of second order, linear, 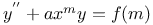 E.6 E.6
Differential equations of second order, linear, 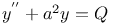 3522 3525 geoMe.66 3522 3525 geoMe.66
Differential equations of second order, linear, 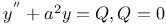 3523—3524 3523—3524
Differential equations of second order, linear, 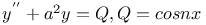 3526 3526
Differential equations of second order, linear, 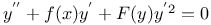 3284 L.42 3284 L.42
Differential equations of second order, linear, 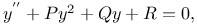 P, Q, R being functions of x 3280 P, Q, R being functions of x 3280
Differential equations of second order, linear, 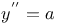 3288 3288
Differential equations of second order, linear, 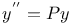 C.9 C.9
Differential equations of second order, linear, 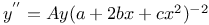 L.44 L.44
Differential equations of second order, linear, 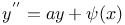 A.45 A.45
Differential equations of second order, linear, 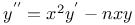 A.53 A.53
Differential equations of second order, linear, 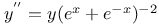 L.46 L.46
Differential equations of second order, linear,  , when , when  are trigonometrical series C.98 are trigonometrical series C.98
Differential equations of second order, linear, 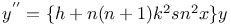 (Lame's eq.) C.85 (Lame's eq.) C.85
Differential equations of second order, linear, 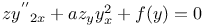 Me.71 Me.71
Differential equations of second order, linear, 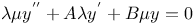 , , 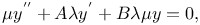 and and 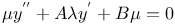 ; with ; with 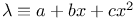 and and 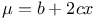 A.42 A.42
Differential equations of second order, linear, homogeneous M.22
Differential equations of second order, linear, integration by Gauss's series Z.19
Differential equations of second order, linear, Py''+Qy'+Ry=0 Ac.1
Differential equations of second order, linear, transformation of An.52
Differential equations of second order, linear, with algebraic integrals C.90 J.81 85 L.76
Differential equations of second order, linear, with doubly periodic coefficients Ac.2
Differential equations of second order, linear, xy''+my'+nxy=0 L.45 78
Differential equations of second order, linear, xy''+y'+y(x+A)=0 Me.81 84
Differential equations of second order, linear, xy''=y Z.2
Differential equations of second order, linear, y''+py'+ry=0 C.85 90 Q.19
Differential equations of second order, linear, y''=ax+by 3281
Differential equations of second order, linear, y''=f(x, y) (Jacobi) 3285
Differential equations of second order, linear, y''=f(y) 3257
Differential equations of second order, polynomials which verify Ac.6
Differential equations of second order, solution by definite integrals A.27
Differential equations of sources AJ.75
Differential equations of third order An.83 C.98 M.23
Differential equations of third order, linear C.88 Q.7 8 14 M.24
Differential equations of third order, linear, 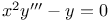 Z.8 Z.8
Differential equations of third order, linear, 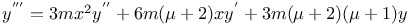 A.42 A.42
Differential equations of third order, linear, 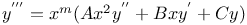 A.58 A.58
Differential equations of third order, linear, 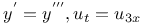 C.3 C.3
Differential equations of third order, linear, y'=y''' JP.15
Differential equations with algebraic integrals J.84
Differential equations with complex variables Mo.85
Differential equations with different. total integrals L.84
Differential equations with fractional indices JP.15
Differential equations with integrals "monochrome and monogene" C.40
Differential equations with quadratic integrals J.99
Differential equations, Abel's theorem J.90
Differential equations, algebraic An.79 C.86
Differential equations, ap. to engineering JP.4
Differential equations, approximate solution C.5
Differential equations, approximate solution, by equations of differences L.37
Differential equations, approximate solution, by Taylor's theorem 3289
Differential equations, asymptotic methods C.94 Q.5
Differential equations, Bessel's numerical solution Z.25
Differential equations, Complete primitive 3163—3166 J.25
Differential equations, Complete primitive, no. of constants CP.9
Differential equations, continuous and discontinuous integrals of C.29
Differential equations, depression of order by unity 3262—3269
Differential equations, elliptic G.19 M.21
Differential equations, elliptic multiplier M.21
Differential equations, exact 3187 3270—3275 G.12 C.1 10 11
Differential equations, general methods L.81
Differential equations, generation of 3150
Differential equations, geometrical meaning of Q.14
Differential equations, homogeneous 3186 3234 3262—3268 C.13 CM.4 J.86
Differential equations, hyperelliptic J.32 55 Mo.62
Differential equations, integrability of Z.12
Differential equations, integrability of, immediate C.82
Differential equations, integrating factors pp468—471 3394 C.68 97
Differential equations, integrating factors of Pdx+Qdy+Rdz Q.2
Differential equations, integration by Bessel's function Me.80
Differential equations, integration by definite integrals 3617—3628 C.17 J.74
Differential equations, integration by differentials of any index C.17 L.44
Differential equations, integration by elimination CP.9
Differential equations, integration by elliptic functions An.79 82 C.41 JP.21
Differential equations, integration by Gamma function TE.20
Differential equations, integration by separation of operative symbols Z.15
Differential equations, integration by series 3604—3616 C.10 94 LM.6 Me.79 Q.19 TI.7
Differential equations, integration by theta-functions C.90
Differential equations, irreducibility of J.92
Differential equations, isoperimeters, pr Mem.50
Differential equations, linear A.28 35 40 41 43 45 46 53 59 65 69 Ac.3 AJ.7 An.50 85 At.75 C.7 29 58 73 84 88 90 91 92 94 CD.3 4 9 CP.9 10 G.15 J.23 24 25 40 42 55 63 70 76 79 80 81 83 87 88 91 98 L.38 64 M.5 11 12 Me.75 P.48 50 51 Pr.5 18 19 20 Q.8 Z.3 7 9
Differential equations, linear, argument & parameter interchanged in the integral J.78
Differential equations, linear, bibliography of AJ.7
Differential equations, linear, determination of arbitrary constant At.65 Q.19
Differential equations, linear, homogeneous Ac.1 J.90 Mo.82
Differential equations, linear, integrating factors of C.97 98
Differential equations, linear, integration by Abelian functions C.92 J.73
Differential equations, linear, integration by finite differences Q.1
Differential equations, linear, integration by series J.76
Differential equations, linear, irreducibility of J.76
Differential equations, linear, Landen's substitution, geo J.91
Differential equations, linear, Malmsten's theorem J.40
Differential equations, linear, n variables, 1st order 3320—3332 C.14 15 G.13 J.20 80 L.38
Differential equations, linear, n variables, 2nd order L.37
Differential equations, linear, n variables, 2nd order, 2 variables C.70
Differential equations, linear, n variables, any order Mem.13
Differential equations, linear, Pdx+Qdy+Rdz=0,  , Q, R similarly with y and z Q.20 , Q, R similarly with y and z Q.20
Differential equations, linear, Pdx+Qdy+Rdz=0, P, Q, R involving x, y, z 3320 geoM.16 Z.20
Differential equations, linear, Pdx+Qdy+Rdz=0, P, Q, R, integral functions of x only Q.19
Differential equations, linear, singular solution J.73 83 84
Differential equations, linear, transformation of C.91 96
Differential equations, linear, which admit of integrals whose logarithmic differentials are doubly periodic functions L.78
Differential equations, linear, which connect a complete function of the 1st kind with the modulus C.86
Differential equations, linear, whose particular integrals are the products of those of two given linear d.e. A.41
Differential equations, linear, with algebraic integrals C.96 97 J.80 90 M.21
Differential equations, linear, with coefficients that are algebraic functions of an independent variable C.92 94
Differential equations, linear, with constant coefficients 3238—3250 An.64 CM.1 2 E.34 JP.33 L.42 N.47 84
Differential equations, linear, with doubly periodic coefficients C.90 92 98 J.90
Differential equations, linear, with periodic coefficients C.91 92
Differential equations, linear, with rational coefficients, algebraic integrals of C.96 JP.32 34
Differential equations, linear, with rational coefficients, upon whose solution depends the quadrature of an irrational algebraic product C.91 92
Differential equations, linear, with variable coefficients C.92 J.66 68 76 L.80 81
Differential equations, linear, without absolute term, condition of solutions in common C.95
Differential equations, linear, xdt+ydx+zdy+tdz=0 A.30
Differential equations, linear, Xdx+Ydy+Zdz+Tdt=0, condition of being an exact differential 3330
Differential equations, Parseval's theorem 3628
Differential equations, particular integrals of CM.2
Differential equations, particular integrals of, algebraic C.86
Differential equations, particular integrals of, relations of the constants C.93 J.10 JP.6
Differential equations, relation between its constants and the constants of a particular solution C.92
Differential equations, rule for equivalence of two solutions 3167
Differential equations, satisfied by the series  . . ![$2\sqrt[4]{q}+2\sqrt[4]{q^{9}}+2\sqrt[4]{q^{25}}+&c.$](/math_tex/538ff01ec472800e468da45fa08e4be282.gif) L.49 J.36 L.49 J.36
Differential equations, satisfying Gauss's function 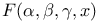 L.82 L.82
Differential equations, simultaneous first order 3340—3349 C.43 J.48 Pr.62
Differential equations, simultaneous linear 3340—3359 AJ.4 C.9 92 E.5 N.66 84
Differential equations, simultaneous linear, 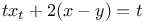 and and 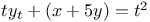 3349 3349
Differential equations, simultaneous linear, 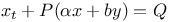 and and 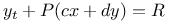 3348 3348
Differential equations, simultaneous linear, 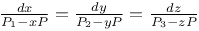 3347 3347
Differential equations, simultaneous linear, 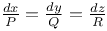 Q.14 Q.14
Differential equations, simultaneous linear, equations in  3357 3357
Differential equations, simultaneous linear, homogeneous in x, y, z... and their second derivatives only 3358
Differential equations, simultaneous linear, Pfaff's method C.14 J.2
Differential equations, simultaneous linear, transformation of J.98
Differential equations, simultaneous system of An.69 82 84 C.10 43 47 92 CM.1 LM.14 Me.13 80 Pr.12
Differential equations, simultaneous system of, 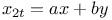 and and 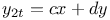 and a similar example 3354 and a similar example 3354
|
 |
|
О проекте
|
|
О проекте



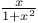

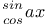
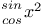
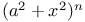
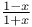
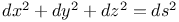
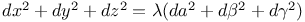
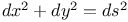 and analogous eqs
and analogous eqs 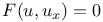
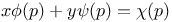
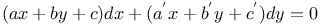
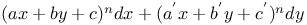
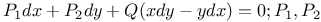 being homogeneous and of the pth deg. in x, y; Q homogeneous and of the qth deg.
being homogeneous and of the pth deg. in x, y; Q homogeneous and of the qth deg. 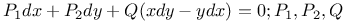 different linear functions of x, y
different linear functions of x, y 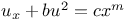 (Riccati's eq.)
(Riccati's eq.) 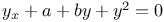
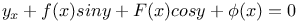
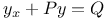 , where P, Q involve x only
, where P, Q involve x only 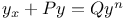
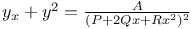 , where P, Q, R are functions of x
, where P, Q, R are functions of x 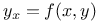
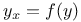
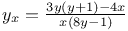
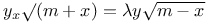
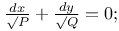 P, Q being quartics in x, y
P, Q being quartics in x, y 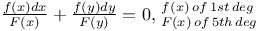
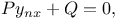 where P, Q are functions of x, y, and the first n-1 derivatives of y
where P, Q are functions of x, y, and the first n-1 derivatives of y 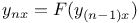
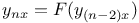
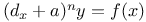
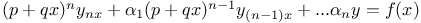
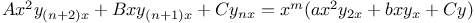
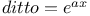
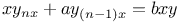
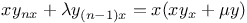
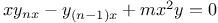
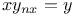
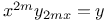
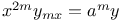
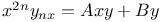
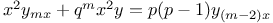
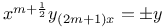 by Bessel's function
by Bessel's function 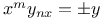 by definite integrals
by definite integrals 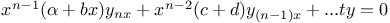
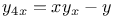
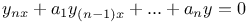
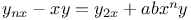 by definite integrals
by definite integrals 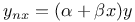
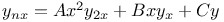
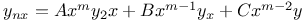
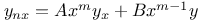
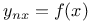
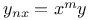
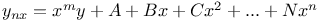
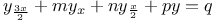
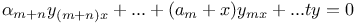
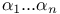 functions of x
functions of x 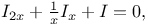 where I is Bessel's function
where I is Bessel's function 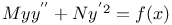
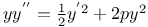
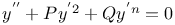
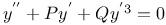 P, Q functions of x
P, Q functions of x 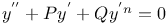
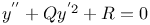
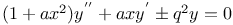
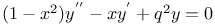

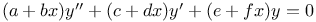
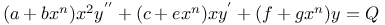 (Pfaff)
(Pfaff) 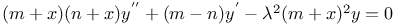
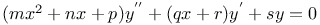
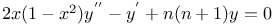
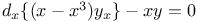
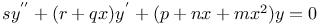
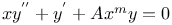
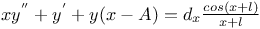
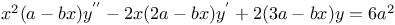
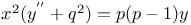
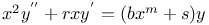
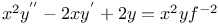
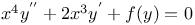
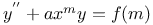
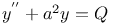
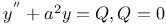
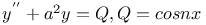
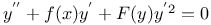
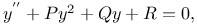 P, Q, R being functions of x
P, Q, R being functions of x 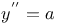
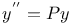
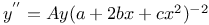
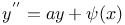
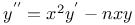
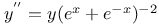
 , when
, when  are trigonometrical series
are trigonometrical series 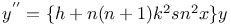 (Lame's eq.)
(Lame's eq.) 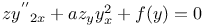
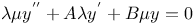 ,
, 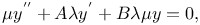 and
and 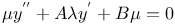 ; with
; with 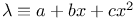 and
and 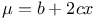
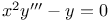
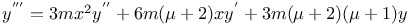
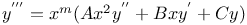
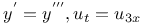
 , Q, R similarly with y and z
, Q, R similarly with y and z  .
. ![$2\sqrt[4]{q}+2\sqrt[4]{q^{9}}+2\sqrt[4]{q^{25}}+&c.$](/math_tex/538ff01ec472800e468da45fa08e4be282.gif)
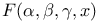
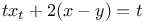 and
and 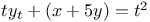
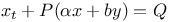 and
and 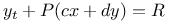
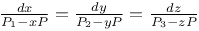
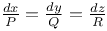

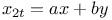 and
and 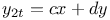 and a similar example
and a similar example