Harmonic progression or proportion, sum of Pr.20
Harmonic section by a quadric and polar plane 5687
Harmonics in a triangle A.57
Helix 5756 A.64
Helix, conical N.13 53
Helix, conical, rectif. of N.45
Helix, relation with cycloid C.51
Helixon a twisted cone A.16
Hemisphere, volume, &c. 6061
Hermite's  function, linear transf. of M.3 function, linear transf. of M.3
Herpolode of Poinsot C.99
Hesse's surface, &c. Z.19
hessian 1630 J.80
Hessian of a quaternary function Q.12
Hessian of a quaternary function, cubic Q.7
Hessian of a surface, nodes of J.59
Hessian of a surface, nodes of, constant of M.23
Hessian, covariant of binary quintic form M.21
Hessian, curve M.13
Hexagon thN.65
Hexagon in space J.85 93
Hexagon, Pascal's see "Pascal"
hexahedron 907
Higher algebra An.54 Q.45
Higher algebra, Serret N.55
Higher analysis A.25 G.14
Higher Arithmetic J.6 9 N.81
Higher geodesy Z.19 trZ.13
Higher geometry A.10 N.57 Z.6 17
Higher planes A.47
Higher variation of simple integrals Z.22
Highest common factor 30 A.3 M.7 N.42 44 45
Highest common factor of 2 complex numbers, no of divisions L.46 48
Highest common factor of 2 polynomials CM.4
Highest common factor, remainder in the process C.42
Holditch's theorem see "Closed curve"
Holomorphic functions C.99 G.22
Holomorphic functions, development in series C.94 M.21
Homalographic projection N.61
Homaloidal system, n-tic surface and an (n-1)-ple point G.13
Homofocal and conjugate surfaces, tr Z.7
Homofocal common tangents of C.22 L.46
Homofocal conics thN.49
Homofocal conics, loci relating to parallel tangents C.62 63
Homofocal quadrics C.50 L.th51 60 N.th64 79 Pr.33
Homofocal quadrics, paraboloids A.35
Homofocal quartic surfaces, triple system of, including the wave surface N.85
Homofocal sphero-conics L.60
Homofocal surfaces, and 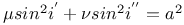 C.22 C.22
Homogeneity of formulae C.96 thsN.49
Homogeneous coordinates G.1 8 Z.15
Homogeneous coordinates, metrical relation G.11
homogeneous functions see "Quantics"
Homogeneous products, H(n, r) 98—99 Q.6 9 10
Homogeneous products, H(n, r) and sums of powers 538 E.39 40
Homographic division of three tangents to a conic Mel.2
Homographic figures threeC.94 thQ.3 N.58 68 pr61
Homographic figures, corresponding points, th L.45
Homographic figures, focal properties LM.2
Homographic figures, relation of roots N.73
Homographic pencils 4651
Homographic systems of points 1058—1073
Homographic systems of points on quadric scrolls Q.9
Homographic theorem of a conic N.48 49
Homographic transformation N.70
Homographic transformation of angles Q.14
Homography Me.62 N.60 Z.21
Homography and perspective N.69
Homography and rotations, correspondence of M.15
Homological polar reciprocal curves ET.44
Homology 975 G.3 8 N.44 E.24
Homology of sets Q.2
Homology of triangles 975 Me.73
Homology, conic of C.94
Homothetic conics 4523 N.64 th68
Homothetic conics with the same centre C.66
Horograph 5826
Hyberbolic arc, rectification of 6115 J.55 P.2 11 59
Hyberbolic arc, rectification of, Landen's theorem 6117 LM.11 13
Hyper-elliptic  -functions, alg. characteristics M.25 -functions, alg. characteristics M.25
Hyper-elliptic functions A.16 AJ.5 7 An.70 C.40 62 67 92 94 97 CD.3 J.25 27 30 40 47 52 54 75 76 81 85 L.54 M.3 11 13 Q.15 19
Hyper-elliptic functions and mechanics J.56
Hyper-elliptic functions in logarithmic algebraic functions M.11
Hyper-elliptic functions of 1st and 2nd kind An.58 J.93
Hyper-elliptic functions of 1st and 2nd kind in series M.9
Hyper-elliptic functions of 1st order J.12 16 35 98
Hyper-elliptic functions of 1st order and 3rd kind J.65 68 88
Hyper-elliptic functions of 1st order, containing transcendents of 2nd and 3rd kind J.82
Hyper-elliptic functions of 1st order, multiplication of Ac.3 M.17 20
Hyper-elliptic functions of 1st order, transformation of Ac.3
Hyper-elliptic functions of 1st order, transformation of 2nd degree M.9 Mo.66
Hyper-elliptic functions of 1st order, transformation of 3rd degree M.1 19
Hyper-elliptic functions of 1st order, transformation of, p=2 M.15
Hyper-elliptic functions of 1st order, transformation of5th degree M.16 17 20
Hyper-elliptic functions of 3rd kind, exchangeability of parameter and argument J.31
Hyper-elliptic functions of 3rd order, p=4 M.12
Hyper-elliptic functions of nth order, algebraic relations C.99
Hyper-elliptic functions of nth order, algebraic relations, Goepel's relation An.82
Hyper-elliptic functions of two arguments, complex mult. of M.21
Hyper-elliptic functions with quartic curves, 4 tables M.10
Hyper-elliptic functions, addition th. for 1st order in a system of confocal quadrics M.22
Hyper-elliptic functions, addition theory M.7
Hyper-elliptic functions, approximation to P.60 62
Hyper-elliptic functions, choice of moduli C.88
Hyper-elliptic functions, division of C.68 98 L.43 M.1
Hyper-elliptic functions, division of, bisection C.70
Hyper-elliptic functions, division of, trisection An.76 M.2
Hyper-elliptic functions, generalisation of C.84 98
Hyper-elliptic functions, geo. representation L.78
Hyper-elliptic functions, inversion of C.99 J.70
Hyper-elliptic functions, periodic J.32
Hyper-elliptic functions, periodic, of the 1st class LM.12
Hyper-elliptic functions, periodic, with four periods An.71
Hyper-elliptic functions, periodicity moduli A.68 An.70
Hyper-elliptic functions, reduction of, to elliptic integrals Ac.4 C.85 93 99 J.55 76 79 86 89 M.15 TI.25
Hyper-elliptic functions, transformation M.7 pr13
Hyper-elliptic functions, transformation of 2nd order, which, applied twice in succession, produces the duplication C.88
Hyper-Fuchsian functions from hypergeometric series of two variables C.99
Hyper-Fuchsian groups C.98
Hyper-geometric functions or series 291 A.55 57 J.15 75 M.3 Q.16 Z.8 26 27
Hyper-geometric functions or series and Jacobi's polynomials C.89
Hyper-geometric functions or series as continued fractions 291—292 J.66
Hyper-geometric functions or series of nth order C.96 J.71 72 M.2
Hyper-geometric functions or series of two variables C.90 91 95 L.82 84
Hyper-geometric functions or series of two variables, extension of Riemann's problem C.90
Hyper-geometric functions or series, square of J.3
Hyper-geometric integrals J.73 Z.22
Hyper-Jacobian surfaces and curves LM.9 P.77 Pr.26
Hyperbola with asymptotes for coord, axes 4387 Me.73
Hyperbola, asymptotic properties 1182
Hyperbola, conjugate 1160
Hyperbola, construction 1247 1289
Hyperbola, eccentric circles A.44
Hyperbola, quadrature of, &c. 6118 A.25 26 27 N.44
Hyperbola, quadrature of, &c., multiple areas TI.7
Hyperbola, rectangular 4392 Z.26
Hyperbola, rectangular under 4 conditions A.3
Hyperbola, segment of 6118 N.61
Hyperbola, theorems A.27 46 CD.1 N.42
Hyperbolic functions 2180 A.19 G.15 Mem.30 N.64
Hyperbolic functions, analogy with the circle An.51
Hyperbolic functions, ap. to evolution and solution of eqs. A.38
Hyperbolic functions, construction of tables of J.16
Hyperbolic functions, generalization of A.35
Hyperboloid 5605 J.85 Me.66
Hyperboloid and relation to ruled surfaces Z.23
Hyperboloid of revolution N.72
Hyperboloid, conjugate CD.2
Hyperboloid, equilateral and of revolution Ac.5
Hyperboloid, generating lines of 5607
| Hyperboloid, one-fold 5605
Hyperboloid, one-fold of rotation A.70 L.39 M.18 N.58
Hyperboloid, one-fold of rotation, parameter of a parabolic section of N.75
Hyperboloid, theorems geoG.4 J.24 86
Hyperboloid, two-fold 5617 A.18 ths27
Hyperboloidic projection of a cubic "gobba" An.63
Hypercycles C.94
Hyperdeterminants CD.9 J.34 42
Hypocycloid 5266
Hypocycloid with 2 cusps Z.19
Hypocycloid with 3 cusps J.64 Me.83 N.70 75
Hypsometric tables of Bessel Pr.12
icosahedron 907 M.12 25
Icosahedron and star dodecahedrons Z.18
Icosian game Q.5
Imaginary 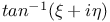 in the form x+iy A.49 in the form x+iy A.49
Imaginary 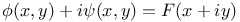 to determine to determine  and and  A.10 A.10
Imaginary ![$\sqrt[3]{}\sqrt{a+ib}$](/math_tex/877de19ea4918011ce24e7ff45def4e182.gif) in the form x+iy A.55 in the form x+iy A.55
Imaginary circular points at infinity 4717 4918 4935 tg.eq4998 5001 Me.68 Q.3 8 32
Imaginary coordinates 4761 C.75 Man.79 homog.Q.18
Imaginary curves Q.7
Imaginary elements in geometrical constructions, and apparent uncertainty therefrom Z.12
Imaginary exponents A.6
Imaginary geometry 4916 A.32 61 C.61 CD.7 8 J.55 70 M.11 Me.81 N.70 72 TE.16
Imaginary geometry of Lobatschewski G.5 J.17 N.68
Imaginary geometry of Standt M.8
Imaginary geometry, use in geometrical drawing J.1
Imaginary integrals of d.e C.23
Imaginary lines through imaginary points 4761 4722—4723
Imaginary prime factors of complex numbers formed from the roots of irreducible rational equations Z.10
Imaginary problem, Newton — Fourier AJ.2
Imaginary quantities 223 A.20 22
Imaginary quantities, 8 square AJ.4 C.18 24 25 88 94 JP.23 N.63 64 P.1 6 31
Imaginary quantities, ap. to primitive functions of some derived functions N.63
Imaginary quantities, conjugates 223
Imaginary quantities, conjugates, modulus of 227
Imaginary quantities, logarithm of 2214 LM.2
Imaginary tangents through the focus of a conic 4720—4721 5008 A.22
Imaginary transformation of coordinates Q.7
Imaginary variables C.96
Imaginary variables, generating polygons of a relation between several JP.30
Imaginary variables, polygons of C.92
Implexes of surfaces C.80
Implicit functions of n independent variables 1737 An.58
Implicit functions of one independent variable, 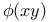 ; values of ; values of 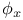 , , 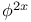 , , 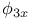 1700—1706 1700—1706
Implicit functions of one independent variable, 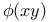 ; values of ; values of 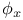 , , 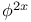 , , 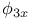 , , 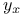 , , 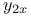 , , 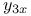 , when , when 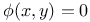 1707—1716 1707—1716
Implicit functions of one independent variable, 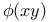 ; values of ; values of 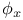 , , 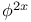 , , 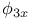 , , 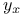 , , 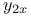 , , 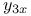 , when , when 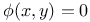 , , 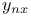 An.58 An.58
Implicit functions of one independent variable, 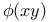 ; values of ; values of 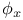 , , 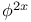 , , 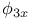 , , 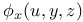 , , 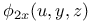 1720—1721 1720—1721
Implicit functions of one independent variable, 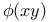 ; values of ; values of 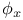 , , 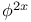 , , 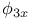 , , 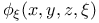 when 3 eqs. connect when 3 eqs. connect 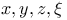 1723 1723
Implicit functions of one independent variable, 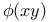 ; values of ; values of 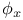 , , 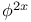 , , 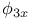 , the same when , the same when 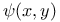 is also given 1718—1719 is also given 1718—1719
Implicit functions of two independent variables, 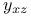 when when 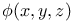 1728 1728
Implicit functions of two independent variables, 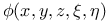 when 3 eqs. connect when 3 eqs. connect 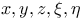 1735 1735
Implicit functions of two independent variables, 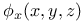 , , 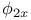 , , 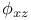 , when , when 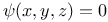 1729—1732 1729—1732
Implicit functions, defined by an alg. eq. C.47
Implicit functions, determined by the infinitesimal calculus C.34
Implicit functions, transf. into explicit functions C.38
Implicit functions, transf. into isotropic means and trig. series C.38
Incommensurable limits of numbers N.81
Incommensurable lines N.44
Incommensurable lines in ratio 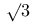 1 A.3 1 A.3
Incommensurable numbers JP.15 N.43
Increment 1484
Indeterminate coefficients 232 1527 A.3 J.5
Indeterminate equations 188—194 C.10 th78 88 G.5 J.9 Mem.44 N.44 45 pr57 59 71 78 81 prs81 85 TE.2 see "Partition"
Indeterminate equations and congruences Pr.11
Indeterminate equations, 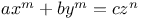 N.79 N.79
Indeterminate equations, 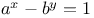 N.57 N.57
Indeterminate equations, 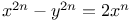 L.40 L.40
Indeterminate equations, 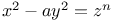 C.99 C.99
Indeterminate equations, 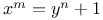 , impossible N.50 70 71 , impossible N.50 70 71
Indeterminate equations, 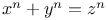 impossible if n>2 (Fermat's last th.) A.26 58 An.64 C.24 89 90 98 J.17 impossible if n>2 (Fermat's last th.) A.26 58 An.64 C.24 89 90 98 J.17
Indeterminate equations, ap. to a geo. problem Mem.20 Z.20
Indeterminate equations, exponential, 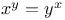 A.6 Z.23 A.6 Z.23
Indeterminate equations, higher degrees, 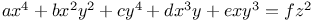 C.88 C.88
Indeterminate equations, higher degrees, 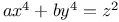 C.87 91 94 N.79 C.87 91 94 N.79
Indeterminate equations, higher degrees, 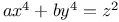 , a=7, b=-5 L.79 , a=7, b=-5 L.79
Indeterminate equations, higher degrees, 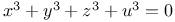 A.49 A.49
Indeterminate equations, higher degrees, 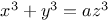 N.78 80 N.78 80
Indeterminate equations, higher degrees, 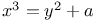 N.78 83 N.78 83
Indeterminate equations, higher degrees, 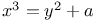 , with a=17 N.77 , with a=17 N.77
Indeterminate equations, higher degrees, 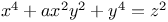 Mem.20 Mem.20
Indeterminate equations, higher degrees, 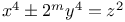 and similar eqs L.53 and similar eqs L.53
Indeterminate equations, higher degrees, 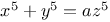 L.43 L.43
Indeterminate equations, higher degrees, 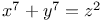 , impossible C.82 L.40 , impossible C.82 L.40
Indeterminate equations, higher degrees, cubic AJ.2
Indeterminate equations, impossible class of N.63
Indeterminate equations, linear JP.13 L.41 N.43 P.61 Z.19
Indeterminate equations, linear, 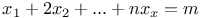 G.1 G.1
Indeterminate equations, linear, with 2 unknowns 188—193 A.3 7 J.42 L.63 69 Mem.31
Indeterminate equations, linear, with 3 unknowns 194 G.2
Indeterminate equations, linear, with n unknowns G.94 N.52
Indeterminate equations, n-tic solution by alg. identities C.87
Indeterminate equations, quadratics in five unknown integers, 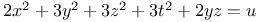 L.66 L.66
Indeterminate equations, quadratics in five unknown integers, 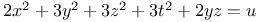 , , 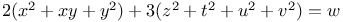 L.64 L.64
Indeterminate equations, quadratics in five unknown integers, 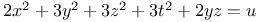 , , 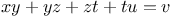 C.62 L.67 C.62 L.67
Indeterminate equations, quadratics in five unknown integers, 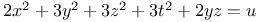 , , 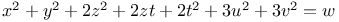 L.64 L.64
Indeterminate equations, quadratics in five unknown integers, 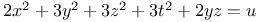 , , 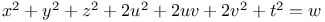 L.64 L.64
Indeterminate equations, quadratics in five unknown integers, 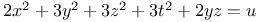 , , 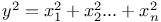 G.7 G.7
Indeterminate equations, quadratics in five unknown integers, 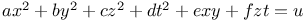 , with the following values of a, b, c, d, e, f: 1, 1, 2, 2, 0, 2; 1, 1, 1, 1, 0, 1; 1, 1, 1, 1, 1, 1; 2, 2, 3, 3, 2, 0; 1, 1, 3, 3, 1, 0 L.63 , with the following values of a, b, c, d, e, f: 1, 1, 2, 2, 0, 2; 1, 1, 1, 1, 0, 1; 1, 1, 1, 1, 1, 1; 2, 2, 3, 3, 2, 0; 1, 1, 3, 3, 1, 0 L.63
Indeterminate equations, quadratics in five unknown integers, 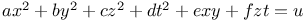 , with the following values of a, b, c, d, e, f: 1, 2, -2, 2, 1, 2 L.63 , with the following values of a, b, c, d, e, f: 1, 2, -2, 2, 1, 2 L.63
Indeterminate equations, quadratics in five unknown integers, 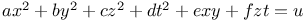 , with the following values of a, b, c, d, e, f: 1, 2, 3, 3, 1, 3; 2, 2, 3, 3, 2, 3; 1, 1, 6, 6, 1, 6 L.64 , with the following values of a, b, c, d, e, f: 1, 2, 3, 3, 1, 3; 2, 2, 3, 3, 2, 3; 1, 1, 6, 6, 1, 6 L.64
Indeterminate equations, quadratics in five unknown integers, 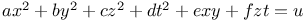 , with the following values of a, b, c, d, e, f: 2, 3, 2, 3, 2, 2; 2, 5, 2, 5, 2, 2 L.64 , with the following values of a, b, c, d, e, f: 2, 3, 2, 3, 2, 2; 2, 5, 2, 5, 2, 2 L.64
Indeterminate equations, quadratics in five unknown integers, 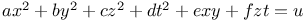 , with the following values of a, b, c, d, e, f: 3, 5, 10, 10, 0, 10; 2, 3, 15, 15, 2, 0; 2, 3, 3, 3, 2, 0 L.66 , with the following values of a, b, c, d, e, f: 3, 5, 10, 10, 0, 10; 2, 3, 15, 15, 2, 0; 2, 3, 3, 3, 2, 0 L.66
Indeterminate equations, quadratics in five unknown integers, 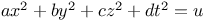 , with the following values of a, b, c, d: 2, 2, 3, 3 L.65 , with the following values of a, b, c, d: 2, 2, 3, 3 L.65
Indeterminate equations, quadratics in five unknown integers, 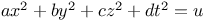 , with the following values of a, b, c, d: 2, 2, 3, 4; 2, 3, 3, 6; 3, 3, 3, 4; 1, 2, 6, 6; 2, 3, 4, 4 L.66 , with the following values of a, b, c, d: 2, 2, 3, 4; 2, 3, 3, 6; 3, 3, 3, 4; 1, 2, 6, 6; 2, 3, 4, 4 L.66
Indeterminate equations, quadratics in five unknown integers, 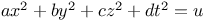 , with the following values of a, b, c, d: 3, 4, 4, 4; 3, 4, 12, 48 L.63 , with the following values of a, b, c, d: 3, 4, 4, 4; 3, 4, 12, 48 L.63
Indeterminate equations, quadratics in five unknown integers, 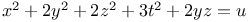 L.64 L.64
Indeterminate equations, quadratics in five unknown integers, 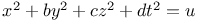 , with the following values of b, c, d: 1, 1, 1; 2, 3, 6 L.45 , with the following values of b, c, d: 1, 1, 1; 2, 3, 6 L.45
Indeterminate equations, quadratics in five unknown integers, 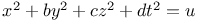 , with the following values of b, c, d: 1, 1, 2; 1, 1, 4; 1, 1, 8; 2, 2, 2; 2, 4, 8; 4, 4, 4; 3, 4, 12 L.61 , with the following values of b, c, d: 1, 1, 2; 1, 1, 4; 1, 1, 8; 2, 2, 2; 2, 4, 8; 4, 4, 4; 3, 4, 12 L.61
Indeterminate equations, quadratics in five unknown integers, 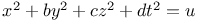 , with the following values of b, c, d: 1, 1, 3; 1, 2, 6; 2, 2, 3; 2, 4, 6; 4, 4, 12; 1, 1, 12; 2, 2, 12; 1, 4, 12; 1, 3, 4; 3, 4, 4; 4, 12, 16; 3, 6, 6; 3, 3, 3; 3, 3, 12; 3, 12, 12; 12, 12, 12 L.63 , with the following values of b, c, d: 1, 1, 3; 1, 2, 6; 2, 2, 3; 2, 4, 6; 4, 4, 12; 1, 1, 12; 2, 2, 12; 1, 4, 12; 1, 3, 4; 3, 4, 4; 4, 12, 16; 3, 6, 6; 3, 3, 3; 3, 3, 12; 3, 12, 12; 12, 12, 12 L.63
Indeterminate equations, quadratics in five unknown integers, 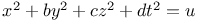 , with the following values of b, c, d: 1, 1, 5; 2, 3, 6; 5, 5, 5 L.46 , with the following values of b, c, d: 1, 1, 5; 2, 3, 6; 5, 5, 5 L.46
Indeterminate equations, quadratics in five unknown integers, 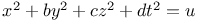 , with the following values of b, c, d: 1, 2, 4; 1, 4, 8; 2, 2, 4; 2, 4, 4; 2, 8, 8; 4, 4, 8; 4, 4, 16; 4, 16, 16; 8, 8, 8; 8, 8, 16; 8, 16, 16; 16, 16, 16 L.62 , with the following values of b, c, d: 1, 2, 4; 1, 4, 8; 2, 2, 4; 2, 4, 4; 2, 8, 8; 4, 4, 8; 4, 4, 16; 4, 16, 16; 8, 8, 8; 8, 8, 16; 8, 16, 16; 16, 16, 16 L.62
Indeterminate equations, quadratics in five unknown integers, 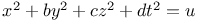 , with the following values of b, c, d: 1, 3, 3 L.60 63 , with the following values of b, c, d: 1, 3, 3 L.60 63
Indeterminate equations, quadratics in five unknown integers, 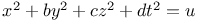 , with the following values of b, c, d: 1, 5, 5; 1, 6, 6; 1, 9, 9; 1, n, n; 2, n, 2n L.65 59 , with the following values of b, c, d: 1, 5, 5; 1, 6, 6; 1, 9, 9; 1, n, n; 2, n, 2n L.65 59
Indeterminate equations, quadratics in five unknown integers, 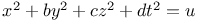 , with the following values of b, c, d: 2, 3, 3; 3, a, 3a L.66 , with the following values of b, c, d: 2, 3, 3; 3, a, 3a L.66
Indeterminate equations, quadratics in five unknown integers, 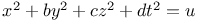 , with the following values of b, c, d: with c=ab C.42 L.56 , with the following values of b, c, d: with c=ab C.42 L.56
Indeterminate equations, quadratics in five unknown integers, 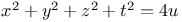 L.56 L.56
Indeterminate equations, quadratics in four unknown integers, 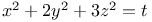 L.69 L.69
Indeterminate equations, quadratics in four unknown integers, 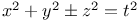 C.66 N.48 C.66 N.48
Indeterminate equations, quadratics in four unknown integers, 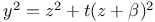 N.78 N.78
Indeterminate equations, quadratics in seven unknown integers, 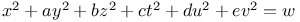 , with the following values of a, b, c, d, e; 1, 1, 1, 1, 1; 1, 1, 1, 1, 2; 1, 1, 1, 2, 2; 1, 2, 2, 2, 2; 2, 2, 2, 2, 2; 2, 2, 2, 2, 4; 3, 3, 3, 3, 3 L.64 , with the following values of a, b, c, d, e; 1, 1, 1, 1, 1; 1, 1, 1, 1, 2; 1, 1, 1, 2, 2; 1, 2, 2, 2, 2; 2, 2, 2, 2, 2; 2, 2, 2, 2, 4; 3, 3, 3, 3, 3 L.64
Indeterminate equations, quadratics in seven unknown integers, 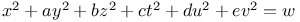 , with the following values of a, b, c, d, e; 4, 4, 4, 4, 4; 1, 4, 4, 4, 4; 2, 2, 4, 4, 4; 1, 1, 4, 4, 4; 1, 2, 2, 4, 4; 1, 1, 1, 4, 4; 1, 1, 2, 2, 4; 1, 1, 1, 1, 4; 4, 4, 4, 4, 16 L.65 , with the following values of a, b, c, d, e; 4, 4, 4, 4, 4; 1, 4, 4, 4, 4; 2, 2, 4, 4, 4; 1, 1, 4, 4, 4; 1, 2, 2, 4, 4; 1, 1, 1, 4, 4; 1, 1, 2, 2, 4; 1, 1, 1, 1, 4; 4, 4, 4, 4, 16 L.65
Indeterminate equations, quadratics in three unknown integers, 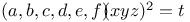 Pr.13 Pr.13
Indeterminate equations, quadratics in three unknown integers, 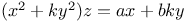 J.49 J.49
Indeterminate equations, quadratics in three unknown integers, 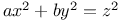 G.8 G.8
Indeterminate equations, quadratics in three unknown integers, 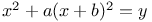 N.78 N.78
Indeterminate equations, quadratics in three unknown integers, 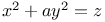 N.78 N.78
Indeterminate equations, quadratics in three unknown integers, 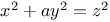 N.78 N.78
Indeterminate equations, quadratics in three unknown integers, 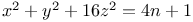 L.70 L.70
Indeterminate equations, quadratics in three unknown integers, 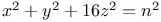 Mel.4 Mel.4
Indeterminate equations, quadratics in three unknown integers, 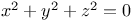 geoA.55 geoA.55
Indeterminate equations, quadratics in three unknown integers, 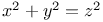 A.22 33 E.30 G.19 A.22 33 E.30 G.19
Indeterminate equations, quadratics in three unknown integers, 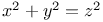 , solution prior to Diophantus C.28 , solution prior to Diophantus C.28
Indeterminate equations, quadratics in three unknown integers, 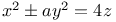 N.72 N.72
Indeterminate equations, quadratics in two unknown integers, 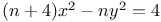 N.83 N.83
Indeterminate equations, quadratics in two unknown integers, 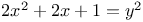 N.78 N.78
Indeterminate equations, quadratics in two unknown integers, 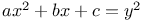 G.7 G.7
Indeterminate equations, quadratics in two unknown integers, 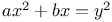 L.76 L.76
Indeterminate equations, quadratics in two unknown integers, 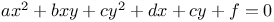 C.87 C.87
Indeterminate equations, quadratics in two unknown integers, 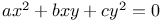 geoC.9 geoC.9
Indeterminate equations, quadratics in two unknown integers, 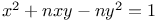 N.83 N.83
Indeterminate equations, quadratics in two unknown integers, 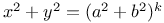 C.36 An.53 C.36 An.53
Indeterminate equations, quadratics in two unknown integers, 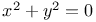 geoA.55 geoA.55
Indeterminate equations, quadratics in two unknown integers, 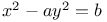 C.69 L.37 38 Mem.28 C.69 L.37 38 Mem.28
Indeterminate equations, quadratics in two unknown integers, 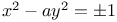 A.12 52 E.23 28 J.17 A.12 52 E.23 28 J.17
Indeterminate equations, quadratics in two unknown integers, 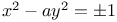 , by trig. L.64—66 N.78 , by trig. L.64—66 N.78
Indeterminate equations, quadratics in two unknown integers, 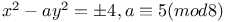 J.53 J.53
Indeterminate equations, quadratics in two unknown integers, 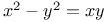 impossible N.46 impossible N.46
Indeterminate equations, quadric J.45
Indeterminate equations, quadric, in n unknowns N.84
|
 |
|
О проекте
|
|
О проекте



 function, linear transf. of
function, linear transf. of 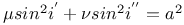
 -functions, alg. characteristics
-functions, alg. characteristics 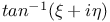 in the form x+iy
in the form x+iy 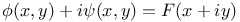 to determine
to determine 
![$\sqrt[3]{}\sqrt{a+ib}$](/math_tex/877de19ea4918011ce24e7ff45def4e182.gif) in the form x+iy
in the form x+iy 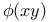 ; values of
; values of 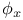 ,
, 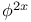 ,
, 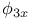
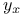 ,
, 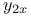 ,
, 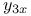 , when
, when 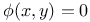
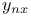
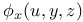 ,
, 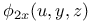
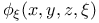 when 3 eqs. connect
when 3 eqs. connect 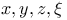
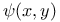 is also given
is also given 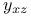 when
when 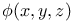
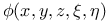 when 3 eqs. connect
when 3 eqs. connect 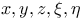
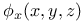 ,
, 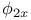 ,
, 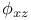 , when
, when 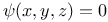
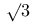
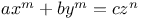
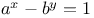
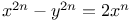
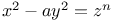
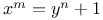 , impossible
, impossible 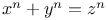 impossible if n>2 (Fermat's last th.)
impossible if n>2 (Fermat's last th.) 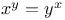
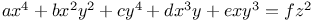
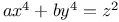
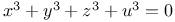
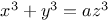
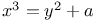
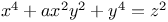
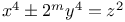 and similar eqs
and similar eqs 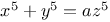
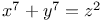 , impossible
, impossible 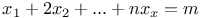
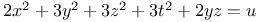
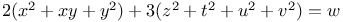
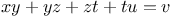
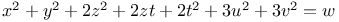
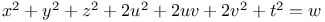
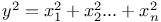
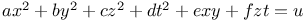 , with the following values of a, b, c, d, e, f: 1, 1, 2, 2, 0, 2; 1, 1, 1, 1, 0, 1; 1, 1, 1, 1, 1, 1; 2, 2, 3, 3, 2, 0; 1, 1, 3, 3, 1, 0
, with the following values of a, b, c, d, e, f: 1, 1, 2, 2, 0, 2; 1, 1, 1, 1, 0, 1; 1, 1, 1, 1, 1, 1; 2, 2, 3, 3, 2, 0; 1, 1, 3, 3, 1, 0 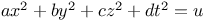 , with the following values of a, b, c, d: 2, 2, 3, 3
, with the following values of a, b, c, d: 2, 2, 3, 3 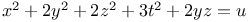
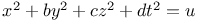 , with the following values of b, c, d: 1, 1, 1; 2, 3, 6
, with the following values of b, c, d: 1, 1, 1; 2, 3, 6 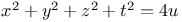
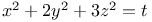
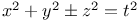
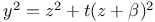
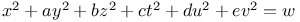 , with the following values of a, b, c, d, e; 1, 1, 1, 1, 1; 1, 1, 1, 1, 2; 1, 1, 1, 2, 2; 1, 2, 2, 2, 2; 2, 2, 2, 2, 2; 2, 2, 2, 2, 4; 3, 3, 3, 3, 3
, with the following values of a, b, c, d, e; 1, 1, 1, 1, 1; 1, 1, 1, 1, 2; 1, 1, 1, 2, 2; 1, 2, 2, 2, 2; 2, 2, 2, 2, 2; 2, 2, 2, 2, 4; 3, 3, 3, 3, 3 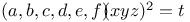
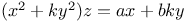
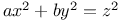
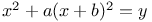
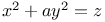
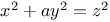
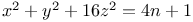
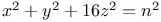
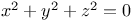
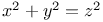
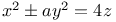
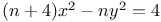
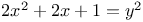
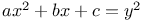
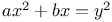
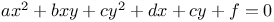
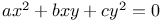
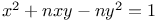
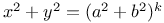
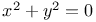
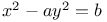
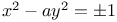
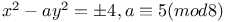
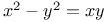 impossible
impossible