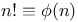Maximum or minimum, solids of max. vol. with given surface and of min. surface with given vol. C.63
Maximum, ellipse touching 4 lines A.12
Maximum, ellipsoid in a tetrahedron Z.14
Maximum, polyhedron in ellipsoid A.32
Maximum, solid of revolution 3074
Maximum, tetrahedron in ellipsoid A.32
Maximum, tetrahedron, whose faccs have given areas C.51 66 N.62
Maximum, volume with a given surface 3082
Mean centre of segments of a line crossing three others A.40
Mean distance of lines from a point Z.11
Mean error of observations A.25 C.37 TI.22
Mean error of observations, in trigonometrical and chain measurements A.46 Z.6
Mean proportionals between two lines A.31 34
Mean values C.18 20 23 26 27 L.67 LM.8 M.6 7 Z.3
Mean values and probabilities, geo C.87 L.79
Mean values of a function of 3 variables C.29
Mean values of a function of one variable G.16
Measures of length &c. 4
Measures of length &c., exactitude of Z.6
Measures of length &c., exactitude of, do. with chain Z.1
Mechanical calculators C.28 I.16 P.85
Mechanical calculators for "least squares" Mel.2
Mechanical construction of 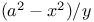 E.18 E.18
Mechanical construction of Cartesian oval AJ.1
Mechanical construction of conformable figures AJ.2
Mechanical construction of conics An.52
Mechanical construction of cubic parabola N.58
Mechanical construction of curves M.6 N.56
Mechanical construction of curves for duplication of roots A.48
Mechanical construction of ellipse A.65 Z.1
Mechanical construction of lemniscate A.3
Mechanical construction of surfaces of 2nd order and class J.34
Mechanical construction of three N.43
Mechanical division of angles Q.4
Mechanical integrators 5450 C.92 94 95 Pr.24
Mechanical integrators for Xdx+Ydy Me.78
Mechanical involution AJ.4
Mechanical measurement of angles A.61
Mechanical quadrature 3772 A.58 59 J.6 63 gzA.66 C.99
Mechanical solution of equations Me.73 N.67
Mechanical solution of equations, cubic and biquadratic, graphically A.1
Mechanical solution of equations, linear simultaneous Pr.28
Mensuration of casks A.20
Metamorphic method by reciprocal radii N.54
Metamorphic transformation N.46
Metrical properties of figures, transf. of N.58 59 60 J.4
Metrical properties of surfaces AJ.4
Metrical system E.30
Meunier's theorem 5809 gzC.74
Minding's theorem, Quaternion proof LM.10
Minimum surfaces eqA.38 G.14 22 J.81 85 87 ext78 Mo.67 72
Minimum surfaces of a twisted quadric At.52
Minimum surfaces, algebraic M.3
Minimum surfaces, algebraic, lowest class-number An.79
Minimum surfaces, arbitrary functions of the integral eq. of C.40
Minimum surfaces, between 2 right lines in space C.40
Minimum surfaces, generation of L.63
Minimum surfaces, limits of (Calc. of Var.) J.80
Minimum surfaces, limits of, determined by one of the edges of a twisted quadrilateral Mo.65
Minimum surfaces, limits of, on a catenoid M.2
Minimum surfaces, metric M.15
Minimum surfaces, not algebraic and containing a succession of algebraic curves C.87
Minimum surfaces, projective M.14
Minimum surfaces, representation of by elliptic functions J.99
Minimum surfaces, variation of surface, capacity of Mo.72
Minimum value of 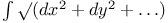 when the variables are connected by a quadric equation J.43 when the variables are connected by a quadric equation J.43
Minimum value of  N.73 N.73
Minimum, theory of L.56 prM.20
Minimum, theory of, angle between two conj. tangents on a positive curved surface A.69
Minimum, theory of, area J.67
Minimum, theory of, area of a hexagonal "alveole", pr N.43
Minimum, theory of, area of circum-polygon CD.3
Minimum, theory of, circum-conic of a quadrilateral A.13 An.54
Minimum, theory of, circum-tetrahedron of an ellipsoid Z.25
Minimum, theory of, circum-triangle of a conic Z.28
Minimum, theory of, circum-triangle of an ellipse Z.25
Minimum, theory of, curves on surfaces J.5 see
Minimum, theory of, distance of 2 right lines G.4
Minimum, theory of, distance of a point, ths A.8
Minimum, theory of, ellipse through 3 points and ellipsoid through 4 L.42
Minimum, theory of, ellipsoid, th Mo.72
Minimum, theory of, N.G.F. of a binary septic AJ.2
Minimum, theory of, numerical value of a linear function with integral coefficients of an irrational quantity C.53 54
Minimum, theory of, perimeter enclosing a given area on a curved surface J.86
Minimum, theory of, questions relating to approximation Mel.2 Mem.59
Minimum, theory of, sum of distances from two points 920 921
Minimum, theory of, sum of squares of distances of a point from three right lines Z.12
Minimum, theory of, sum of squares of functions N.79
Models LM.39
Models of ruled surfaces Me.74
Modular equations An.79
Modular equations of 8th degree 59 C.48 49 66 M.1 2 Mo.65 see
Modular factors of integral functions N.24
Modular functions and integrals An.51 J.18 19 20 21 23 25 M.20
Modular indices of polynomials, which furnish the powers and products of a binomial eq N.25
Modular relations At.65
Modular, degradation of M.14
Modulus of functions, principal N.20
Modulus of series N.17
Modulus of transformations 1604 A.17
Moment of inertia 5903 An.63 At.43 M.23
Moment of inertia by geometry of 4 dimensions Q.16
Moment of inertia of a quadrilateral 5951 Q.11
Moment of inertia of a tetrahedron 5957
Moment of inertia of a triangle 5944 Me.4 Q.6
Moment of inertia of a triangle, polar N.83
Moment of inertia of ellipsoid 6150 CD.8 J.16
Moment of inertia of solid rings of revolution Q.16
Moment of inertia of various laminae and solids 6015—6165
Moment of inertia, principal axes 5926 5967 5972 At.43
Momental ellipse 5953
Momental ellipsoid 5925 5934
Momental ellipsoid for a plane 5936
Monge's theory "des Deblais et des Remblais" LM.14
Monocyclic systems and related ones J.98
Monodrome functions C.43 G.18
Monogenous functions (Laurent's th) Ac.4 C.32 43
Monothetic equations C.99
Monotypical functions C.32
Mortality A.39
Movements JP.15
Movements of "ahnlich - veraenderlicher" and "affin-veraenderlicher" systems Z.24 19
Movements of a plane figure thAn.68 JP.20 28 LM.3
Movements of a point on an ellipsoid AJ.1 J.54
Movements of a right line C.89 N.63
Movements of a solid JP.21
Movements of an invariable system C.43
Movements, elliptic and parabolic JP.30
Movements, groups of An.69
Movements, relative JP.19
Movements, relative, of a point L.63
Movements, transmission of and the curves resulting JP.3
Multinomial theorem 137 Me.62
Multiple curves of alg. surfaces An.73
Multiple Gauss sums J.74
Multiple integrals 1905 2825 A.64 An.52 C.8 11 thsCD.1 thE.36 J.69 L.39 43 45 46 th48 56 LM.8 Me.76 Z.1 3
Multiple integrals 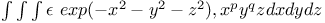 N.54 N.54
Multiple integrals  with limits 0 to with limits 0 to  in each case (Pfaff) J.28 in each case (Pfaff) J.28
Multiple integrals 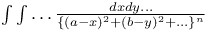 by discontinuous functions TI.21 by discontinuous functions TI.21
Multiple integrals 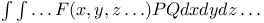 where where 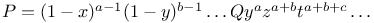 L.59 L.59
Multiple integrals of theory of attraction CD.7
Multiple integrals which are unaltered in form by transformation of the variables J.15 91
Multiple integrals, 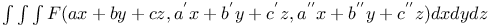 , limits , limits 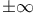 A.30 A.30
Multiple integrals, 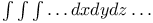 Q.23 Q.23
Multiple integrals, 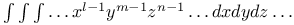 with different limiting equations 2825 CM.2 L.51 with different limiting equations 2825 CM.2 L.51
Multiple integrals, arising from (2604), viz: 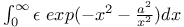 Pr.42 Pr.42
Multiple integrals, do. with 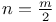 and with a numerator and with a numerator 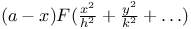 CM.3 CM.3
Multiple integrals, double 2710 2734—2742 A.13 Ac.5 An.70 J.27 G.10 L.58 Mem.30
Multiple integrals, double, 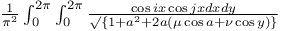 C.96 C.96
Multiple integrals, double, 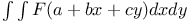 A.37 A.37
| Multiple integrals, double, 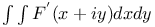 J.42 J.42
Multiple integrals, double, 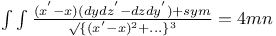 C.66 C.66
Multiple integrals, double, 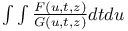 C.96 C.96
Multiple integrals, double, 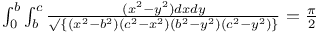 L.38 L.38
Multiple integrals, double, 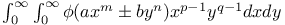 J.37 J.37
Multiple integrals, double, approximation to J.6
Multiple integrals, double, Cauchy's theory, ext. of C.75
Multiple integrals, double, change of order of integration 2775 A.19
Multiple integrals, double, expressing an arbitrary function J.43
Multiple integrals, double, reduction of J.45 Z.9
Multiple integrals, double, residues of C.75
Multiple integrals, double, same with log of numerator L.50
Multiple integrals, double, transf. of 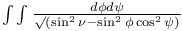 J.20 J.20
Multiple integrals, evaluation A.5
Multiple integrals, evaluation by Fourier's th CM.4
Multiple integrals, expansion of Q.8
Multiple integrals, Frullanian LM.15
Multiple integrals, limits of LM.16
Multiple integrals, reduction of An.57 L.41 39
Multiple integrals, reduction of, 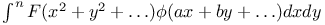 L.57 L.57
Multiple integrals, reduction of, by transf. of coordinates C.13
Multiple integrals, some other integrals evaluated by  functions 2826 2834 functions 2826 2834
Multiple integrals, transformation of 2774 A.10 An.53 No.47 CM.4 Mel.2 Mem.38 Q.4 12
Multiple integrals, transformation of, 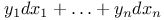 LM.11 LM.11
Multiple integrals, transformation of, a triple integral 2774 2779 J.45
Multiple integrals, transformation of, an indef. double J.8 10
Multiple integrals, triple 2774 A.30 J.45
Multiple integrals, volume integral of 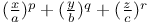 Z.14 Z.14
Multiple points 5178 CM.2 thG.15 Me.2 Q.2 6
Multiple points on a surface J.28
Multiple points on algebraic curves An.52 L.42 N.51 59 81
Multiple points on algebraic curves at  64 64
Multiple points on two curves having branches in contact C.77
Multiple-centres, geo. theory L.45
Multiplication 28 J.49
Multiplication by fractions Me.68
Multiplication, abridged N.79
Multiplicator equations M.15
Multiplicity or manifoldness J.84 86 thAc.5 Z.20
MUSIC E.27 28 Pr.37
Nasik squares and cubes Q.8 15
Navigation, geo. prs. of use in A.38
Negative in geometry No.1792
Negative quantities At.55 N.44 67 TE.1788
Nephroid LM.10
Net surfaces J.1 2 M.1
Net surfaces and series C.62
Net surfaces, any order An.64
Net surfaces, having a 3-point contact with the intersection of two algebraic surfaces G.9
Net surfaces, quadric J.70 82 M.11
Net surfaces, quartic M.7
Net surfaces, trigonometrical Z.14
Newton, autograph m.s.s of TE.12
Nine-point circle 954 4754 A.41 E.7 30 th35 pr39 G.1 ths4 Me.64 68 Q.5—8
Nine-point circle and 12-point sphere, analogy N.63
Nine-point circle, an analogous circle A.51
Nine-point circle, contact with in- and ex-circles 959 Me.82 Q.13
Nine-point conic of a tetrahedron Me.71
Nodal cones of quadrinodal cubics Q.10
Node cusps Q.6
Nodes, two-plane and one-plane M.22
Non-uniform functions C.88
Nonions (analogous to Quaternions) C.97 98
Normals 1160 4122—4123 5122 A.13 53 LM.9 p.eMe.66 Z.cn2 3
Normals of a surface 5771 5785 C.52 CD.3 CM.2 L.39 47 72 M.7
Normals of a surface, coincident L.48
Normals of envelopes Me.80
Normals of rational space curves J.74
Normals, plane of a surface 5772
Normals, principal 5722
Normals, principal, condition for being normals of a second curve C.85
Normals, section of ellipsoid (geodesy) A.40
Normals, transformation of a pencil of C.88
Notation A, B, C, F, G, H 1642 see
Notation for some developments C.98
Notation, 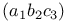 554 554
Notation, 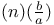 , Jacobi's function see "Functions" , Jacobi's function see "Functions"
Notation, 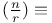  th coeff. of nth power of (1+x) also Jacobi's function see "Functions" th coeff. of nth power of (1+x) also Jacobi's function see "Functions"
Notation, 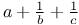 160 160
Notation, 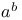 or or 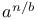 2451 2451
Notation, 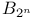 , Bernoulli's nos. 1539 , Bernoulli's nos. 1539
Notation, 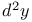 , , 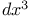 , , 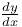 ,&c. 1407 ,&c. 1407
Notation, 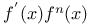 424 1405 424 1405
Notation, 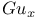 3732 3732
Notation, 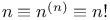 94 3713 94 3713
Notation, 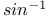 , &c. 626 , &c. 626
Notation, 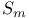 , , 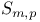 534 534
Notation,  2940 2940
Notation, 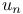 3499 3499
Notation, 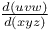 1600 1600
Notation, 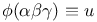 4656 4656
Notation, 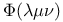 or U 4665 or U 4665
Notation,  as operator 3500 as operator 3500
Notation, 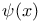 or or 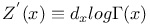 2743 2743
Notation,  3781—3783 3781—3783
Notation,  582 1641 3701 582 1641 3701
Notation, ( I ) and ( X ) 1620
Notation, A.P., G.P., H.P. 79 83 87
Notation, algebraic CP.3
Notation, C(n,r) or 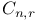 96 96
Notation, D 3489
Notation, D, 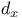 , , 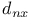 , &c. 1405 , &c. 1405
Notation, E 902 3735
Notation, f(x) 400 1400
Notation, f(x), 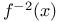 430 430
Notation, H(n,r) 98
Notation, J 1600
Notation, P(n,r) or 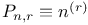 95 95
Notation, R, r, 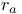 909—913 909—913
Notation, sinh, &c. 2180
Notation, subfactorial Me.78
Notation, suggestions Me.73
Numbers 349 A.2 16 26 58 59 Ac.2 AJ.4 6 C.f12 43 44 45 f60 CM.1 G.16 32 J.9 39 40 48 77 tr 27 28 29 JP.9 L.37—39 41 45 58 59 60 LM.4 Mem.22 24 tr(Euler) 30 N.44 62 79 Q.4 TE.23 see "Indeterminate
Numbers of  function No.81 function No.81
Numbers of infinitesimal analysis J.19 21
Numbers, 4m+1 and 4m+3 divisors of a number LM.15
Numbers, ap. of algebra JP.11
Numbers, approximation to 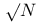 E.17 E.17
Numbers, approximation to functions of large numbers C.82
Numbers, binomial eqs. with a prime mod C.62
Numbers, cube Q.4
Numbers, cubic binomials: 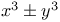 C.61 C.61
Numbers, determined by continued fractions LM.29
Numbers, digits terminating a power A.58 N.46
Numbers, digits, calculus of, th J.30
Numbers, Dirichlet's f. for class numbers as positive determinants L.57
Numbers, Dirichlet's th. 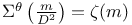 L.57 L.57
Numbers, division of A.26 J.13 Mel.3 Pr.7 10
Numbers, division of, by 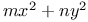 Mem.15 P.17 88 Q.19 20 Mem.15 P.17 88 Q.19 20
Numbers, division of, by 7 and 13 A.25 26
Numbers, divisors arising from the division of the circle L.60
Numbers, divisors of 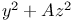 when A=4n+3 a prime J.9 when A=4n+3 a prime J.9
Numbers, factors of Mem.41
Numbers, formulae L.64 65
Numbers, Gauss's form L.56
Numbers, integral quotients and remainders An.52
Numbers, large, analysis of A.2 C.2 29
Numbers, method with continuous variables J.41
Numbers, multiples of C.2
Numbers, non-pentagonal th J.31
Numbers, number of integers prime to n in 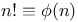 L.57 L.57
Numbers, odd A.1
Numbers, odd and prime to all squares C.67
Numbers, Pellian equation prA.49 LM.15
Numbers, Pellian equation, sol. by ell. functions Mo.63
Numbers, perfect C.81 N.79
Numbers, polygonal, Fermat's th. of P.61
Numbers, polynomials having determinate prime divisors C.98
Numbers, powers of, 12 theorems N.46
Numbers, prime to and < N A.3 29 E.28 J.31 N.45
|
 |
|
О проекте
|
|
О проекте



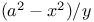
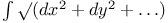 when the variables are connected by a quadric equation
when the variables are connected by a quadric equation 
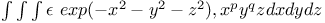
 with limits 0 to
with limits 0 to  in each case (Pfaff)
in each case (Pfaff) 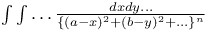 by discontinuous functions
by discontinuous functions 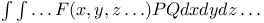 where
where 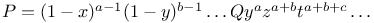
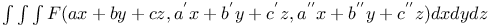 , limits
, limits 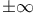
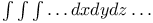
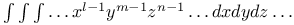 with different limiting equations
with different limiting equations 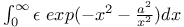
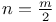 and with a numerator
and with a numerator 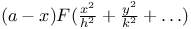
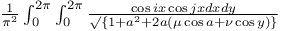
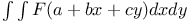
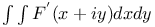
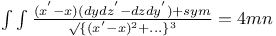
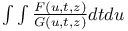
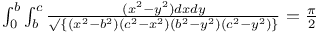
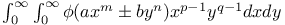
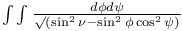
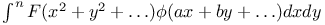
 functions
functions 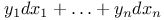
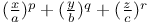
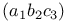
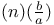 , Jacobi's function
, Jacobi's function 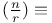
 th coeff. of nth power of (1+x) also Jacobi's function
th coeff. of nth power of (1+x) also Jacobi's function 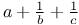
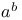 or
or 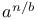
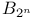 , Bernoulli's nos.
, Bernoulli's nos. 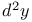 ,
, 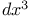 ,
, 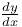 ,&c.
,&c. 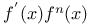
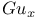
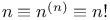
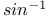 , &c.
, &c. 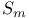 ,
, 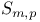

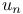
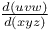
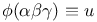
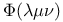 or U
or U  as operator
as operator 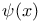 or
or 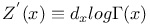


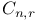
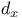 ,
, 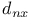 , &c.
, &c. 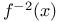
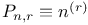
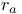
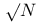
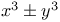
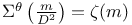
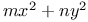
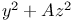 when A=4n+3 a prime
when A=4n+3 a prime