Elliptic functions, quadriquadric curve M.25
Elliptic functions, reduction of An.64
Elliptic functions, reduction of, in canonical forms J.53
Elliptic functions, relations A.67 J.56
Elliptic functions, relations between 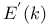 and and 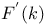 J.39 J.39
Elliptic functions, representation by power series J.54
Elliptic functions, representation of quantities by sin am(u+w, k) J.45
Elliptic functions, series C.95
Elliptic functions, sn 8u, cn 8u, dn 8u in terms of sn u, tables Pr.33
Elliptic functions, sn, cn, and dn of u+v+w LM.13
Elliptic functions, spherical triangle of Q.19
Elliptic functions, subsidiary, pm (u, k) LM.15
Elliptic functions, substitution of 1st order J.34
Elliptic functions, transformation An.57 58 60 Ac.3 C.49 f79 f80 82 CD.3 5 J.3 34 35 f55 55 87 88 89 LM.9 11 M.14 19 22 Me.83 tr84 Pr.27 Q.13 20
Elliptic functions, transformation and division J.76 M.25
Elliptic functions, transformation and of functions in theory of Catenary A.2
Elliptic functions, transformation by roots of unity J.6
Elliptic functions, transformation Hermite's; tables J.72
Elliptic functions, transformation Jacobi's LM.15 16 J.87
Elliptic functions, transformation of 11th order At.5
Elliptic functions, transformation of 1st and 2nd kind as functions of the mod L.40
Elliptic functions, transformation of 1st kind A.33
Elliptic functions, transformation of 3rd order J.60 Me.83
Elliptic functions, transformation of 7th order, square of mod J.12 LM.13
Elliptic functions, transformation of a double integral, &c. Me.75
Elliptic functions, transformation of rectangular coordinates LM.15
Elliptic functions, transformation of the orders 11 13 17 19 J.12 16
Elliptic functions, transformation, cubic C.64 Q.13
Elliptic functions, transformation, linear J.91
Elliptic functions, transformation, modular, of Abel, ap to conics C.79
Elliptic functions, transformation, modular, of Abel, ap to geom C.58
Elliptic functions, transformation, modulus of in a function of the quotient of the two periods An.70
Elliptic functions, transformation, pertaining to an even number J.14
Elliptic functions, transformation, quartic Q.12
Elliptic functions, triple division of and ap. to inflex. of cubics A.70
Elliptic functions, Weierstrass's method AJ.6
Emanents 1654
Empirical formulae, calculation of Me.73
Engrenages L.39 40
Envelope 5192 A.24 prs56 C.45 86
Envelope from ellipse and circle LM.15
Envelope of a carried curve 5239
Envelope of a curve with n parameters 5194
Envelope of a plane C.35
Envelope of a quadric Q.11
Envelope of a right line N.63 79 83 Q.13
Envelope of a right line, cutting two circles harmonically N.85
Envelope of a right line, sliding on two rectangular axes N.45
Envelope of a Simson line E.29 34
Envelope of a sphere C.67 J.33
Envelope of a sphere, touching 3 spheres N.60
Envelope of a surface CM.1 M.5
Envelope of a surface of revolution L.65
Envelope of a surface, degree of N.60
Envelope of chord of a closed curve E.28
Envelope of chord of a closed curve, cutting of a constant area E.31
Envelope of chords of a conic N.48
Envelope of chords of a conic, subtending a constant angle at the focus CM.3
Envelope of conics, theorems N.45
Envelope of curves in space L.83
Envelope of directrix of a parabola E.34
Envelope of geodesics M.14 20
Envelope of pedal line of a triangle Q.10
Envelope of pedal line of a triangle, do. of in-triangle of a circle Q.8 9
Envelope of perpendiculars at extremities of diameter of an ellipse N.46
Envelope of plane curves G.11 12
Envelope of plane curves, singularities of LM.2
Envelope of planes perpendicular to radiants of an ellipsoid at the surface An.59 Pr.9
Envelope of planes which cut a quartic gauche curve of the 2° in 4 points of a circle An.71
Envelope of polars of a curve J.58
Envelope of tangent of 2 variable circles N.51
Envelope, application to perspective A.9
Envelope, class of (Chasles), th C.85
Envelope, imaginary, of the conjugates of a plane curve C.75
Envelope, p.d.e CM.4 G.11 M.84 Me.64 72 N.44 59 68 74
Enveloping asymptotic chords and polars A.14 16 17
Enveloping cone 5664—5672
Enveloping cone of a quadric 5697
Enveloping cone of a quadric, th of Jacobi J.12 CD.3
Enveloping cone of a twisted hexagon, locus of vertex A.10
Enveloping cone of an n-tic surface CD.4
Enveloping line of class cubic, involution th E.29
Epi- and Hypo-cycloids 5266—5272 LM.4 Z.18
Epi- and Hypo-cycloids and derived curves Z.17
Epi- and Hypo-cycloids, tangential properties of absPr.34
Epi- and Hypo-trochoids 5262—5265 LM.4
Epicycloids J.1 Mem.20 N.45 46 60 TE.24 thsZ.15
Epicycloids, centre of curvature N.59
Epicycloids, centre of curvature, plane and spherical JP.14
Epicycloids, double generation of N.69
Epicycloids, reciprocal polar of geoE.19
Equality and similarity of figures J.52
Equations 50—67 211—222 400—594 A.6 18 57 58 60 61 65 67 tr AJ.6 An.51 54 C.44 see
Equations (For Binomial, Biquadratic, Cubic, Cubic and biquadratic, Linear, Quadratic, Quintic, and Transcendental) 47 59 62 68 91 97 99 CM.3 CP.4 G.1 J.13 16 34 L.67 69 M.14 21 Me.76 Mo.79 f80 N.67 68 ths55 67 80 P.1799
Equations from observations A.21
Equations in geo. mean of roots N.45
Equations in one variable 45—58 214—216 400—550
Equations in one variable, approx A.20
Equations in one variable, approx 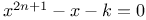 An.59 An.59
Equations in one variable, approx, graphic solution C.65
Equations in quotients of roots N.45
Equations in sums of the C(n, 2) roots of another eq. N.43
Equations in three variables, 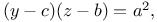 sym in x, y, z 219 sym in x, y, z 219
Equations in three variables, 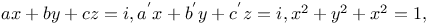 by trigonometry A.6 by trigonometry A.6
Equations in three variables,  , sym A.35 , sym A.35
Equations in three variables,  , sym, and x=cy+bz &c., sym 221—222 , sym, and x=cy+bz &c., sym 221—222
Equations in three variables,  , sym 220 , sym 220
Equations in three variables, gn.sol 60 A.1 64 N.47 M.37
Equations in three variables, gn.sol by acubo-cycloid C.69
Equations in two variables 59—67 211 217—218 A.20 25 CM.2 J.14 N.47 48 63 Pr.8 Q.18
Equations in two variables of any degree with a variable parameter L.59
Equations in two variables, 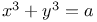 and and 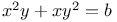 A.48 A.48
Equations in two variables, implicit Mem.30
Equations in two variables, numerical solution Z.20
Equations of degree above the 4th not soluble J.83
Equations of geometry C.68
Equations of geometry, homogeneous N.64
Equations of nth degree with two real roots C.98
Equations of payments A.34 36 CD.1 CM.2
Equations with integral coefficients 503 C.24 J.53
Equations with integral, complex coefficients J.53
Equations with only one positive root 411 C.98
Equations, 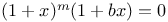 when x is small A.2 when x is small A.2
Equations, 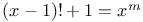 L.56 L.56
Equations, 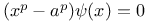 N.82 N.82
Equations, 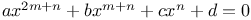 G.14 G.14
Equations, 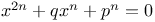 and derivatives N.65 and derivatives N.65
Equations, 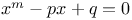 : number of real roots C.98 : number of real roots C.98
Equations, 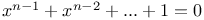 irreducible if n be a prime L.56 irreducible if n be a prime L.56
Equations, Abel's properties C.91
Equations, algorithms for solving M.3
Equations, derived 424—431 A.22
Equations, derived in d.e 1708—1712
Equations, developments An.61
Equations, differential operators in LM.14
Equations, Eisenstein's theorem LM.7
Equations, extension of theory of C.58
Equations, fundamental principles or theorems A.1 11 C.96 97 L.39 40 J.23
Equations, Galois' theory C.60 G.12 M.18 23
Equations, generic Q.4 5
Equations, Hariot's law of J.2 extC.98
Equations, homogeneous, reduction of a principal function which verifies a characteristic homog. eq. C.13 14
Equations, identical J.27
Equations, impossible Man.51
Equations, insolubility of quintics, &c. J.1
Equations, irrational Man.51
Equations, irreducible An.51 Mo.80
Equations, irreducible, of prime degrees AJ.7
Equations, linear see "Linear equations"
Equations, miscellaneous 214
| Equations, numerical C.10 12 32 78 81 G.13 J.10 L.36 38 41 83
Equations, numerical and commensurable quadratic factors L.45
Equations, reciprocal 466 A.44 C.16
Equations, reciprocal of a quartic N.66
Equations, reduction of C.97 CD.6
Equations, reduction of, to reciprocal eqs. A.35
Equations, relation to linear d.e and f.d.e L.36
Equations, simultaneous 59 211 582 C.25 LM.6 thsN.48 81 see "Equations
Equations, simultaneous, deducible the one from the other C.22
Equations, simultaneous, of the form 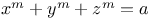 N.46 N.46
Equations, simultaneous, quadratics N.60
Equations, solution by approximation 506—533 A.30 Ac.4 C.11 17 45 60 79 82 E.4 G.8 J.14 22 Me.68 N.51 62 78 80 84 No.58 P.5 Q.3 TI.7 Z.23
Equations, solution by continued fractions J.33
Equations, solution by definite integrals Me.81 P.64 Z.3
Equations, solution by diminishing the powers of the roots C.41
Equations, solution by elimination of integers N.70
Equations, solution by geometry C.87
Equations, solution by imaginary values J.20
Equations, solution by infinite series J.33
Equations, solution by interpolation C.5
Equations, solution by logarithms C.95
Equations, solution by radicals C.58 Q.15
Equations, solution by series An.57 C.49 52 J.6 Mem.33
Equations, solution by transcendents An.63 Q.5
Equations, solution by trigonometry 480 A.1
Equations, solution of 45 54 59 211 466—533 582 A.64 trAn.52 C.3 5 62 64 J.4 27 87 Mo.56 61
Equations, solution of a nonic eq. which has this characteristic: A given rational symmetrical function 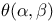 of two roots, gives a third root of two roots, gives a third root 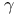 , such that , such that 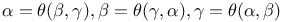 J.34 J.34
Equations, solution of the one by the other C.72 L.71
Equations, solution of, Horner's method 533 P.19
Equations, solution of, Lagrange's method 525 C.91
Equations, solution of, Newton — Fourier method 527—528 AJ.4 G.2 Me.66 N.46 56 60 69 79
Equations, solution of, Weddle's method Z.7 8
Equations, symbolic, non-linear C.22
Equations, systems of C.67 G.11 18 LM.2 8 Q.11 M.19 Z.14 18 see
Equations, transformation of C.64
Equations, whose coefficients are rational functions of a variable J.74
Equations, whose degree is a power of a prime An.61 C.48 L.68
Equiangular spiral 5288 Me.62 N.69 70
Equilateral hyperbolic paraboloid and derived ray-system Z.23
Equimultiples in proportion G1
Equipollences, method of N.69 70 73 74
Equipotential curves Me.82 Pr.24
Equipotential surfaces G.20 geoJ.42 M.8
Equipotential surfaces of ellipsoid L.82
Equivalence of forms C.88 90 JP.29
Equivalent representation Z.23
Equivalents, theory of A.44
Eratosthenes' crib or sieve N.43 49
Error in final digit of decimals C.40 Me.74 N.56
Errors of constants Mo.83
Errors of observation A.18 19 An.58 C.93 JP.13 N.56 P.70 TE.24
Euclid, enunciations p.xxi
Euclid, enunciations, axiom 11 J.1 I.47
Euclid, enunciations, axiom 11, new proof C.60
Euclid, enunciations, II 12 and 13, new proof Q.9
Euclid, enunciations, II. 12 and 13 Me.80 VI.7 Q.11
Euclid, enunciations, XI., &c. Me.71 XI.28 A.10
Euclid, enunciations, XII., &c. G.9
Euclid, enunciations, XII., criticism on Q.7 9
Euler's algorithms A.67
Euler's constant 2744 Pr.15 16 18 19 20 Table
Euler's constant and Binet's function C.77 L.75
Euler's equation N.72
Euler's equation, integration of it by the lines of curvature of a ruled hyberboloid N.75
Euler's equations of motion solved by elliptic integrals Q.14
Euler's formula for 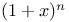 L.44 L.44
Euler's integrals 2280—2323 A.41 Ac.1 2 An.54 C.9 17 94 95 th96 J.15 21 45 fL.43 Me.83 Z.9
Euler's integrals, 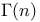 see "Gamma function" see "Gamma function"
Euler's integrals, ap. to series and functions of large numbers JP.16
Euler's integrals, B(l, m) 2280 An.69 G.9
Euler's integrals, sum formula and quadratic residues An.52
Euler's numbers AJ.5 An.77 C.66 83 J.79 89 prsL.44 Me.78 80
Evectant of Hessian of a curve E.32
Even and odd functions 1401
Evolute 5149—5159 5165 An.53 61 C.30 Q.3 11
Evolute and involute in one L.41
Evolute of a catenary 5159
Evolute of a cubic curve Q.11
Evolute of a cycloid A.30
Evolute of a parabola 4549 4959 Q.5 N.65
Evolute of a tortuous curve 5731 A.25
Evolute of a tortuous curve, angle of torsion of evolute 5754
Evolute of a tortuous curve, integrable equations L.43
Evolute of an ellipse 4547 4958 C.84 N.52 63
Evolute of an evolute, in inf. L.59 Me.80
Evolute of negative focal pedal of a parabola E.29
Evolute of surfaces C.74
Evolute of symmetrical bicircular quartics Q.18
Evolute of the limacon, rectif. and quadr. of E.40
Evolute, analogous curves L.76
Evolute, oblique, direct and inverse of different orders C.85
Evolute, rectification and quadrature of A.4
Evolution 35
Ex-circle of a triangle 711 953 4749 A.54 thN.60
Ex-circle of a triangle, focus of centre, th Q.9
Expansion of 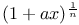 in an integral series A.65 in an integral series A.65
Expansion of 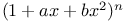 Q.18 Q.18
Expansion of 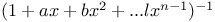 AJ.6 AJ.6
Expansion of 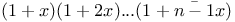 C.25 J.43 C.25 J.43
Expansion of 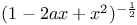 L.37 L.37
Expansion of 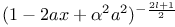 C.86 C.86
Expansion of  J.43 J.43
Expansion of 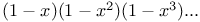 C.92 J.21 L.42 C.92 J.21 L.42
Expansion of 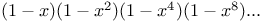 Me.80 Me.80
Expansion of 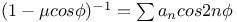 A.21 A.21
Expansion of 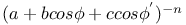 in cosines of multiples of in cosines of multiples of 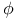 and and 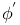 J.15 J.15
Expansion of  At.57 At.57
Expansion of 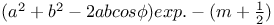 TE.5 TE.5
Expansion of 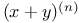 CM.3 CM.3
Expansion of 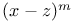 in powers in powers 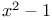 C.86 C.86
Expansion of 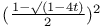 in powers of t, when in powers of t, when 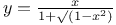 1565 1565
Expansion of 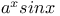 in differences of sin x 3749 in differences of sin x 3749
Expansion of 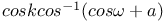 C.15 C.15
Expansion of  A.47 A.47
Expansion of 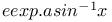 1535 1535
Expansion of 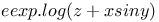 1557 1557
Expansion of 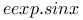 1529 1529
Expansion of 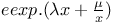 Z.3 Z.3
Expansion of 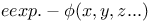 C.58 C.58
Expansion of 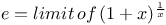 1590 A.3 23 Q.7 1590 A.3 23 Q.7
Expansion of 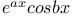 798 798
Expansion of 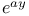 in powers of in powers of 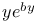 1571 1571
Expansion of 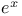 C.30 N.48 C.30 N.48
Expansion of 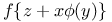 in powers of x (Lagrange) 1552 in powers of x (Lagrange) 1552
Expansion of 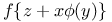 in powers of x (Lagrange), Laplace's th 1556 in powers of x (Lagrange), Laplace's th 1556
Expansion of 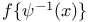 and and 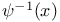 1561—1563 1561—1563
Expansion of 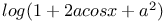 2922 2922
Expansion of 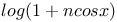 2933 2933
Expansion of  155—159 155—159
Expansion of 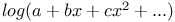 1537 1537
Expansion of 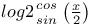 2927 2927
Expansion of 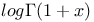 2294 2773 2294 2773
Expansion of 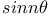 and and 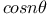 in powers of in powers of 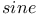 or or 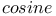 , , 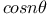 in powers of cos in powers of cos 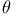 780 Q.12 780 Q.12
Expansion of 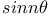 and and 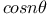 in powers of in powers of 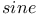 or or 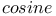 , , 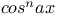 A.11 A.11
Expansion of 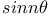 and and 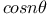 in powers of in powers of 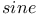 or or 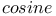 , , 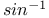 1528 1564 J.25 N.74 1528 1564 J.25 N.74
Expansion of 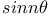 and and 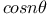 in powers of in powers of 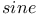 or or 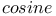 , , 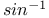 , remainder Z.1 , remainder Z.1
Expansion of 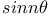 and and 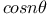 in powers of sine or cosine 758 775—779 1533 C.82 CM.2 Me.76 Mem.13 15 18 N.73 83 Q.4 in powers of sine or cosine 758 775—779 1533 C.82 CM.2 Me.76 Mem.13 15 18 N.73 83 Q.4
Expansion of 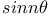 and and 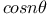 in powers of sine or cosine, convergency of the series J.4 in powers of sine or cosine, convergency of the series J.4
Expansion of 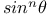 and and 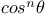 in sines or cosines of multiple arcs 772—774 A.24 55 C.12 CD.3 J.1 5 14 N.71 TI.7 in sines or cosines of multiple arcs 772—774 A.24 55 C.12 CD.3 J.1 5 14 N.71 TI.7
Expansion of 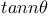 760 760
Expansion of  791 791
Expansion of 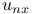 in differences of u 3752 in differences of u 3752
Expansion of 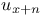 3740 3740
Expansion of 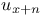 , , 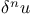 3761 3761
Expansion of 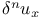 and and 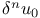 3741—3742 3741—3742
Expansion of 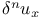 and and 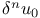 in differential coefficients of u 3751 in differential coefficients of u 3751
Expansion of 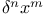 and and 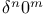 3743—3734 3743—3734
Expansion of 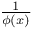 (Cayley) 1555 (Cayley) 1555
Expansion of 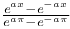 2962 2962
Expansion of 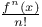 , by Taylor's th CM.4 , by Taylor's th CM.4
|
 |
|
О проекте
|
|
О проекте



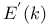 and
and 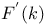
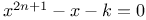
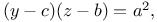 sym in x, y, z
sym in x, y, z 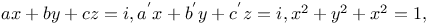 by trigonometry
by trigonometry , sym
, sym  , sym, and x=cy+bz &c., sym
, sym, and x=cy+bz &c., sym  , sym
, sym 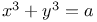 and
and 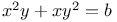
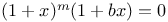 when x is small
when x is small 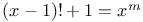
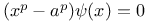
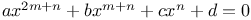
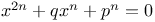 and derivatives
and derivatives 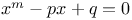 : number of real roots
: number of real roots 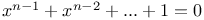 irreducible if n be a prime
irreducible if n be a prime 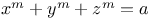
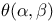 of two roots, gives a third root
of two roots, gives a third root 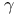 , such that
, such that 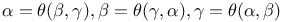
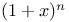
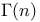
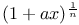 in an integral series
in an integral series 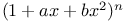
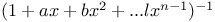
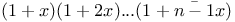
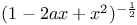
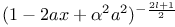

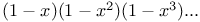
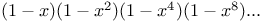
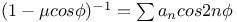
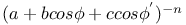 in cosines of multiples of
in cosines of multiples of 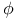 and
and 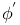

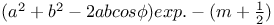
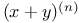
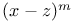 in powers
in powers 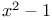
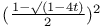 in powers of t, when
in powers of t, when 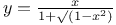
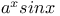 in differences of sin x
in differences of sin x 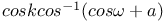

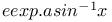
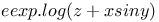
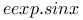
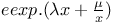
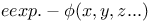
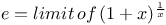
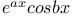
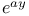 in powers of
in powers of 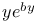
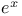
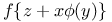 in powers of x (Lagrange)
in powers of x (Lagrange) 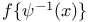 and
and 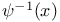
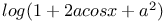
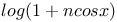

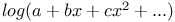
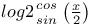
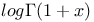
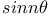 and
and 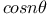 in powers of
in powers of 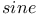 or
or 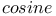 ,
, 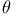
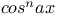
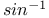
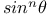 and
and 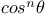 in sines or cosines of multiple arcs
in sines or cosines of multiple arcs 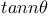

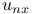 in differences of u
in differences of u 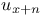
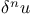
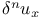 and
and 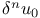
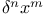 and
and 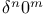
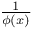 (Cayley)
(Cayley) 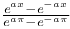
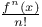 , by Taylor's th
, by Taylor's th