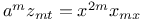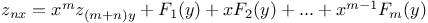Numbers, prime to and < the product of the first n primes A.66
Numbers, prime to the radix having multiples made up of repeating digits Me.76
Numbers, prime with respect to a given ar.p C.54
Numbers, products of divisors of Q.20
Numbers, quadratic forms of Mem.53
Numbers, rational linear functions taken with respect to a prime modulus, and connected substitutions C.48
Numbers, relation of the theory to i.c C.82
Numbers, representation of by forms C.92
Numbers, representation of by infinite products A.1
Numbers, square having prime factors of the form 4n+1 N.78
Numbers, squares of J.84 M.13 Pr.6 7
Numbers, squares of, three in ar.p N.62
Numbers, sum and difference of two squares thsN.63
Numbers, sums depending upon E(x) L.60
Numbers, sums of digits Me.66 TE.16
Numbers, sums of divisors 377 Ac.6 G.7 L.63 Mel.2 Mem.50
Numbers, sums of powers of 276 2939 An.61 65 thCD.5 Me.75 N.42 56 70 Q.8 see
Numbers, sums of powers of 4th powers A.54
Numbers, sums of powers of cubes An.65 L.66
Numbers, sums of powers of n primes N.79
Numbers, sums of powers of squares A.67
Numbers, sums of powers of the odd nos. A.64
Numbers, sums of powers of uneven orders Mo.57
Numbers, symmetrical functions of Q.7
Numbers, systems Z.14
Numbers, systems, history of, by Humboldt J.4
Numbers, theorems A.7 10 20 49 An.70 C.25 43 83 CM.2 G.8 L.48 52 N.75
Numbers, theorems on 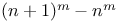 N.44 N.44
Numbers, theorems on 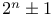 N.85 86 Me.78 N.85 86 Me.78
Numbers, theorems on 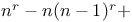 , &c. 285 A.30 , &c. 285 A.30
Numbers, theorems on 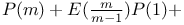 Q.3 Q.3
Numbers, theorems on 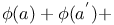 , &c.=n, where a, a', &c., are the divisors of n Cm.3 , &c.=n, where a, a', &c., are the divisors of n Cm.3
Numbers, theorems on 2, 4, 8, and 16 squares Q.17
Numbers, theorems on 2m positive numbers N.43
Numbers, theorems on 4 squares N.57
Numbers, theorems on an odd sum of 12 squares L.60
Numbers, theorems on products of sums of squares G.2
Numbers, theorems on the greatest product in whole numbers of given sums J.57
Numbers, theorems, 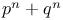 in terms of pq N.75 in terms of pq N.75
Numbers, theorems, 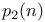 L.69 L.69
Numbers, theorems, 2, biquadratic character of C.57 66 L.59
Numbers, theorems, Cauchy's gzC.53
Numbers, theorems, Eisenstein's J.27 50 83 LM.7 Q.5 6
Numbers, theorems, Gauss's on 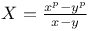 C.98 C.98
Numbers, theorems, Lagrange's arithmetical A.47
Numeration, ancient decimal C.6 8
Numerical approximations N.42 53
Numerical functions L.57 Me.62
Numerical functions, simply periodic AJ.1
Numerical functions, sums of, approximately C.96
Numerical functions, which express for a negative determinant the number of classes of a quadratic form, one at least of whose extreme coefficients is odd C.62
Obelisks A.9 11
Oblique and osculating circle of a conic G.22
Oblique, bevilled wheels, cn J.2
Oblique, coordinates 4050 5511—5519 fN.54
Oblique, cyclic surface TI.9
Octahedron function Q.16
Octahedron, centroid of LM.9
Octic equations G.7 10
Octic equations and curves M.15
Octic surface G.13 M.4 Q.14
Operative or symbolic calculus 1483 3470—3628 AJ.4 C.17 G.20 J.5 59 LM.12 Me.82 85 P.37 44 60—63 Pr.10 11 12 13 Q.4 5 8
Operative or symbolic calculus on the symbols 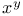 , , 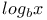 , sin x, cos x, , sin x, cos x, 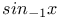 , , 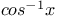 A.9 11 A.9 11
Operative or symbolic calculus, algebraic TE.14
Operative or symbolic calculus, algebraic, 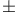 CM.3 CM.3
Operative or symbolic calculus, algebraic, ap. to geometry CM.1 2
Operative or symbolic calculus, applications G.19 Me.82
Operative or symbolic calculus, expansions Pr.14
Operative or symbolic calculus, formulae C.39
Operative or symbolic calculus, index symbol 1485 CD.6
Operative or symbolic calculus, integration CD.3 exMe.76
Operative or symbolic calculus, representation of functions C.43 CD.2
Operative or symbolic calculus, seminvariant operators Q.20
Operative or symbolic calculus, theorems A.57 CD.8 LM.11 Q.3 15 16
Operative or symbolic calculus, theorems, from 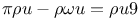 CD.5 CD.5
Operative or symbolic calculus, theorems, from Lagrange's series Q.16
Operators, 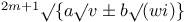 , &c. C.96 , &c. C.96
Operators, 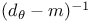 , &c. 3470—3485 , &c. 3470—3485
Operators, 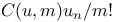 3514 3514
Operators, 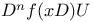 E.36 E.36
Operators, 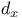 1405 1405
Operators, 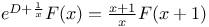 E.36 E.36
Operators, 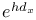 1520—1521 Q.9 1520—1521 Q.9
Operators, 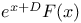 , &c. E.34 , &c. E.34
Operators, 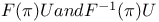 3509—3510 3509—3510
Operators, 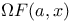 Q.13 Q.13
Operators,  3500 3500
Operators, 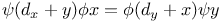 3498 3498
Operators, 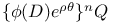 3491 3491
Operators, D(D-1)...(D-n+1) 3489
Operators, expansions and formulae for 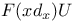 , where , where 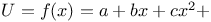 3486 3486
Operators, f(D)uv 3494
Operators, f(x+hD).1 E.39
Operators, gz of 3474 C.43
Operators, reduction of 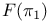 3503 3503
Operators, transformation of 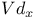 , , 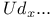 , &c G.21 , &c G.21
Operators, uf(D)v 3495
Orthocycle Q.17
Orthogonal circle and conic E.7
Orthogonal circles 4170 4182—4184
Orthogonal circles, of in- and circum-circles of a triangle Q.18
Orthogonal conics N.84
Orthogonal conics, families of A.63
Orthogonal coordinates C.60
Orthogonal coordinates, curvilinear JP.26
Orthogonal curves J.35 N.52 81
Orthogonal curves, system from logarithmic representation Z.16
Orthogonal lines and conics C.72
Orthogonal lines of a triangle 4633
Orthogonal projection 1087
Orthogonal projection in metrical projective geometry GM.14
Orthogonal projection of a circle into an ellipse A.2
Orthogonal projection of a triangle E.30 31 36 37
Orthogonal substitution J.67 M.13 Z.24
Orthogonal surfaces C.29
Orthogonal surfaces and isothermal C.84 JP.18 L.43 49
Orthogonal surfaces with elliptic coordinates C.53 J.62
Orthogonal surfaces, cubic eq. for C.76
Orthogonal surfaces, spheres 36 54 59 72 79 87 ths17 21 J.84 JP.17 L.43 44 46 47 63 N.51 P.73 Pr.21 Q.19
Orthogonal surfaces, systems C.67 75 M.7
Orthogonal surfaces, systems, condition J.83
Orthogonal surfaces, systems, parallel M.24
Orthogonal surfaces, systems, quadric J.76
Orthogonal surfaces, triple A.55—58 An.63 77 85 C.alg58 67
Orthogonal surfaces, triple, cyclic G.21 22 J.84
Orthogonal surfaces, triple, quartic 82 Z.23
Orthogonal trajectories L.45 Me.80 Z.17
Orthogonal trajectories of a moveable plane Pr.41
Orthogonal trajectories of a moveable sphere C.42
Orthogonal trajectories of a surface Mem.20
Orthogonal trajectories of circles Me.85
Orthogonal trajectories of circular sections of an ellipsoid L.47
Orthogonal, coefficient system A.2 61
Orthogonals, algebraic system of C.69
Orthomorphic projection of an ellipsoid on a sphere AJ.3
Orthomorphosis of a circle into a parabola Q.20
Orthoptic lines of a conic A.57
Orthoptic surface of a quadric J.50
Orthoptic, loci of LM.13 Pr.37
Orthoptic, loci of, of 3 tangs. to a quadric E.40
Orthotomic circles Me.64 66 Q.2
Osculating circle 5724 L.39
Osculating circle of a family of curves N.70
Osculating circle of a parabola, ths N.66
Osculating circle of conics A.70 N.60
Osculating circle of quadric curves N.43
Osculating circle of tortuous curves N.81
Osculating cone 5727
Osculating cone, angle of 5752
Osculating conic L.39
| Osculating conic, of a cubic curve J.68 Z.17
Osculating conic, triply A.69 Z.19
Osculating curves Q.11
Osculating helix N.71
Osculating line of a surface C.82 J.81
Osculating parabola N.81
Osculating paraboloid JP.15 N.82
Osculating paraboloid of a quadric L.38
Osculating plane 5721
Osculating plane and radii of curv. at a multiple point of a gauche curve An.71 C.68
Osculating plane of a tortuous curve C.96 J.41 63
Osculating plane, eq 5733
Osculating sphere Mem.20 N.70
Osculating sphere of curve of intersection of two surfaces, cn C.83
Osculating sphere of two curves having a common principal normal LM.16
Osculating surfaces C.79
Osculating surfaces of quadrics N.60
Osculating surfaces, degree of 98 L.41 80
Oval of Cassini see "Cassinian oval"
Oval of Descartes see "Cartesian oval"
P.D.E., any order No.73 C.80 89 M.11 13
P.D.E., any order and ap. to physics JP.13
P.D.E., any order and elliptic functions J.36
P.D.E., any order and elliptic functions, hyper-ell. J.99
P.D.E., any order of cylinders Me.77
P.D.E., any order of dynamics C.5 J.47
P.D.E., any order of heat L.48
P.D.E., any order of heat, of sound L.38
P.D.E., any order of Laplace G.23
P.D.E., any order of orthogonal systems of surfaces Ac.4 C.77
P.D.E., any order of physics L.72 47
P.D.E., any order with periodical coefficients C.29
P.D.E., any order, 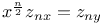 Z.7 Z.7
P.D.E., any order, any number of functions and independent variables C.80
P.D.E., any order, Hamiltonian M.23 Z.11
P.D.E., any order, integrated in series C.15 16
P.D.E., any order, integration by definite integrals An.59 C.94 L.54
P.D.E., any order, linear An.77 C.13 90 CD.9 CM.2 J.69 JP.12 L.39
P.D.E., any order, two independent variables C.75 CP.8
P.D.E., first order 3399—3410 A.33 tr50 An.55 69 C.14 53 54 CD.7 CM.12 J.2 17 trJP.22 L.75 M.9 11 th20 Z.22
P.D.E., first order and Poisson's function C.91
P.D.E., first order, 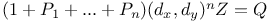 Z.13 Z.13
P.D.E., first order, 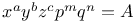 CM.1 CM.1
P.D.E., first order, 3 variables J.64
P.D.E., first order, complete primitive connected with any solution 3405
P.D.E., first order, derivation of a singular solution from the differential equation 3403
P.D.E., first order, derivation of the general primitive and singular solution from the complete primitive 3401
P.D.E., first order, integration by Abelian functions C.94
P.D.E., first order, integration by Cauchy's method C.81
P.D.E., first order, integration by Charpit's method 3399
P.D.E., first order, integration by Jacobi — Hamilton method M.3
P.D.E., first order, integration by Jacobi's first method C.79 82
P.D.E., first order, integration by Jacobi's first method and ap. to Pfaff's pr J.59
P.D.E., first order, integration by Lie's method M.6 8
P.D.E., first order, integration by Weiler's method M.9
P.D.E., first order, law of reciprocity 3446
P.D.E., first order, linear 3381—3395
P.D.E., first order, linear, 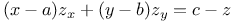 3392 3392
P.D.E., first order, linear, 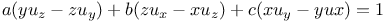 Q.8 Q.8
P.D.E., first order, linear, 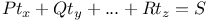 3387 3387
P.D.E., first order, linear, 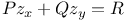 3383 3383
P.D.E., first order, linear, 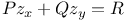 , extension to n variables 3384 , extension to n variables 3384
P.D.E., first order, linear, 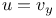 and and 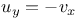 J.70 J.70
P.D.E., first order, linear, 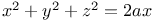 3393 3393
P.D.E., first order, linear, 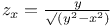 ; ; 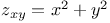 3390—3391 3390—3391
P.D.E., first order, linear, L(px + qy - z) - Mp - Nq + R=0 C.83
P.D.E., first order, linear, reduction to C.15 J.81 Me.78
P.D.E., first order, linear, simultaneous 3396—3397
P.D.E., first order, linear, simultaneous, ex. 3398 J.81
P.D.E., first order, n variables 3409 A.22 J.60 LM.10 11
P.D.E., first order, n variables with constant coefficients Mel.5
P.D.E., first order, n variables, integration by calc. of variations C.14
P.D.E., first order, simultaneous C.68 76 L.79 M.4 5
P.D.E., first order, singular solution 3401—3403 J.66
P.D.E., first order, systems of A.56 M.11 17
P.D.E., first order, theorem of Jacobi C.45
P.D.E., first order, with a general first integral Me.78
P.D.E., first order, z=px+qy+F(p,q) Z.5
P.D.E., fourth order 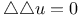 C.69 C.69
P.D.E., second order 3420—3445 A.33 C.54 70 78 98 JP.tr22 L.72 M.15 Me.76 77 Mel.3 N.83 P.46
P.D.E., second order, 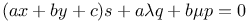 A.33 A.33
P.D.E., second order, 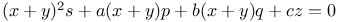 A.33 38 A.33 38
P.D.E., second order, 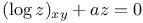 C.36 C.36
P.D.E., second order, 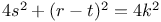 approx. integn. C.74 approx. integn. C.74
P.D.E., second order, 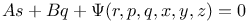 C.93 C.93
P.D.E., second order, 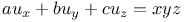 , &c. 3554 , &c. 3554
P.D.E., second order, 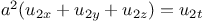 3629 C.7 LM.7 3629 C.7 LM.7
P.D.E., second order, 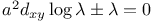 L.53 L.53
P.D.E., second order, 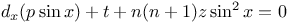 L.46 L.46
P.D.E., second order, 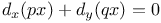 Z.28 Z.28
P.D.E., second order, 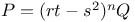 , Poisson's eq. 3441 , Poisson's eq. 3441
P.D.E., second order, 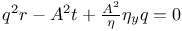 E.22 E.22
P.D.E., second order, 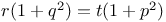 J.58 J.58
P.D.E., second order, 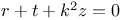 M.1 M.1
P.D.E., second order, 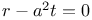 3433 3433
P.D.E., second order, 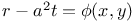 , &c. 3565 , &c. 3565
P.D.E., second order, 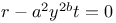 E.27 28 E.27 28
P.D.E., second order, 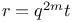 C.98 C.98
P.D.E., second order, 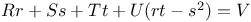 3424 3434—3440 J.61 3424 3434—3440 J.61
P.D.E., second order,  geoQ.2 geoQ.2
P.D.E., second order, 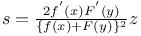 C.81 C.81
P.D.E., second order, 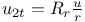 where where 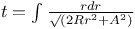 L.38 L.38
P.D.E., second order, 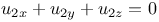 3551 3626 J.36 Mo.78 see 3551 3626 J.36 Mo.78 see
P.D.E., second order, 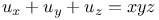 3552 3552
P.D.E., second order, 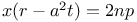 E.13 E.13
P.D.E., second order, 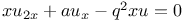 3618 3618
P.D.E., second order, 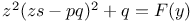 A.70 A.70
P.D.E., second order, (1+r)t+(1+t)r-2pqs=0 An.53
P.D.E., second order, construction of explicitly integrable equations of the form 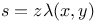 JP.28 JP.28
P.D.E., second order, in 4 and 5 variables Mem.13
P.D.E., second order, in two independent variables trA.54 trNo.81 C.92
P.D.E., second order, in two independent variables, transf. of 97 M.24
P.D.E., second order, integration by change of variables C.74
P.D.E., second order, q(1+q)r+p(1+p)t-(p+q+2pq)s=0 3432
P.D.E., second order, r+t=0 A.2 CM.1 J.59 73 74 L.43
P.D.E., second order, r=q J.72
P.D.E., second order, Rr+Ss+Tt+Pp+Qq+Zz=U 3442
P.D.E., second order, Rr+Ss+Tt=V, Monge's method 3423 CM.3 N.76 Q.6
P.D.E., second order, s+ap+bq+abz=V 3444
P.D.E., second order, s+Pp+Qq+Z=0 Me.76
P.D.E., second order, transf. of C.97
P.D.E., simultaneous C.92 th78 LM.9 M.23 Z.20
P.D.E., simultaneous, linear J.65
P.D.E., system of C.13 74 81
P.D.E., system of, 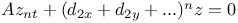 C.94 C.94
P.D.E., system of, 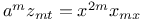 A.30 31 A.30 31
P.D.E., system of, 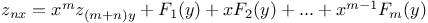 A.51 A.51
P.D.E., system of, dz=Hdx+Kdy+Ldp+Mdq+Ndr+ &c. J.14
P.D.E., third order, two independent variables LM.8 N.83
Pangeometry G.5 15
Pantograph 5423 Mem.31 TE.13
Paper currency A.42
Pappus, prs in plane geometry A.38 Z.5
Parabola anal. 4200—4239 eqCM.2 N.42 54 70
Parabola anal., geo CM.4 Me.71 cn1249 thsN.60 63 71 76 80
Parabola and right line see "Right line"
Parabola geo. 1220—1244
Parabola in space A.3
Parabola, chords of 1239 4224
Parabola, chords of, two intersecting 1242
Parabola, circle of curvature of 1260 A.61
Parabola, circum-hexagon and triangle CM.1
Parabola, determination of vertex and axis N.58
Parabola, eq. deduced from eq. of ellipse 1219
Parabola, focal chord 4235—4239
Parabola, focus and directrix N.49
Parabola, latus rectum 1222 Me.75
Parabola, normal, length of 4233—4234
Parabola, plane and spherical A.60
Parabola, quadrature of 1244 A.32
|
 |
|
О проекте
|
|
О проекте



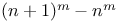
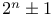
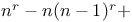 , &c.
, &c. 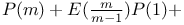
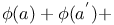 , &c.=n, where a, a', &c., are the divisors of n
, &c.=n, where a, a', &c., are the divisors of n 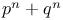 in terms of pq
in terms of pq 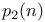
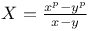
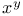 ,
, 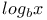 , sin x, cos x,
, sin x, cos x, 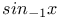 ,
, 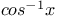
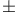
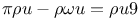
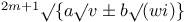 , &c.
, &c. 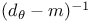 , &c.
, &c. 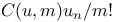
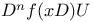
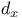
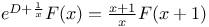
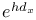
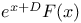 , &c.
, &c. 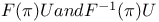
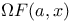

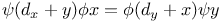
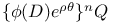
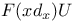 , where
, where 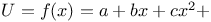
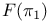
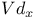 ,
, 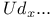 , &c
, &c 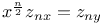
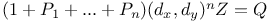
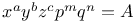
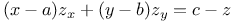
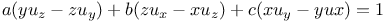
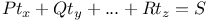
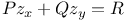
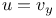 and
and 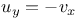
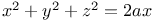
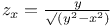 ;
; 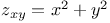
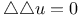
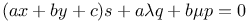
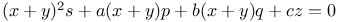
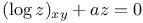
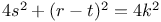 approx. integn.
approx. integn. 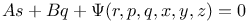
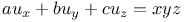 , &c.
, &c. 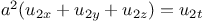
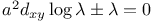
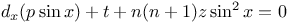
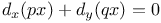
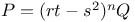 , Poisson's eq.
, Poisson's eq. 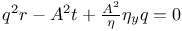
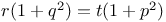
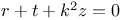
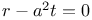
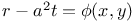 , &c.
, &c. 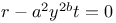
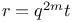
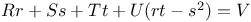

 where
where