|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Misner C.W., Thorne K.S., Wheeler J.A. — Gravitation |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Radio sources, cosmic 759—762
Radio sources, cosmic isoiropy on sky 703 (see also “Quasars”)
Radius of closed Friedmann universe 704f
Raising indices see “Index manipulations”
Rays, in geometric optics 573ff 581f
Redshift Doppler 63f 794
Redshift due to “ether drift” 1064f
Redshift of radiation from a collapsing star 847 849f 872
Redshift parameter, z, denned 187
Redshift, cosmological contrasted with Doppler shift 794
Redshift, cosmological derivations from standing waves 776
Redshift, cosmological derivations from wave-crest emission, propagation, and reception 777f
Redshift, cosmological derivations using symmetry-induced constant of geodesic motion 777 780
Redshift, cosmological in anisotropic cosmology 801 (see also under “Cosmology”)
Redshift, cosmological independent of wavelength 775
Redshift, cosmological of cosmic microwave radiation 764—765 779
Redshift, cosmological of particle energies and de Broglie waves 780
Redshift, cosmological used to characterize distances and times in universe 779
Redshift, cosmological “tired light” does not explain 775
Redshift, gravitational, for gravitational waves 956f 968
Redshift, gravitational, for photons compared with 1970 clock technology 1048
Redshift, gravitational, for photons derivation from energy conservation 187
Redshift, gravitational, for photons equivalence principle tested by 189f 1056
Redshift, gravitational, for photons experimental results 1058 1060
Redshift, gravitational, for photons from geodesic equation in generic static metric 657 659
Redshift, gravitational, for photons geodesic motion tested by 1055—1060
Redshift, gravitational, for photons implies spacetime is curved 187—189
Redshift, gravitational, for photons in linearized theory 446f
Redshift, gravitational, for photons in solar spectum 1058—1060
Redshift, gravitational, for photons Pound — Rebka-Snider experiment 1056—1058
Redshift, gravitational, for temperature 568 685
Reference system see “Coordinate system” “Inertial “Lorentz “Proper
Regge calculus, applications and future of 1178—1179
Regge calculus, blocks associated with one hinge 1170
Regge calculus, choice of edge lengths 1177—1178
Regge calculus, choice of lattice structure 1173—1177
Regge calculus, continuum limit of 1169
Regge calculus, count of faces 1177
Regge calculus, Einstein’s geometrodynamic law, expressed in 1173
Regge calculus, facing, packing, and right-through blocks 1176
Regge calculus, flow diagram for 1171—1172
Regge calculus, geometry determined by lengths 1167
Regge calculus, hinges 1169
Regge calculus, initial-value data in 1172
Regge calculus, simplexes and deficit angles 1167—1169
Regge calculus, skeleton geometry 1169
Regge calculus, suitable for low-symmetry geometrodynamics 1166
Regge calculus, supplementary vertices in 1176
Regge calculus, surveyed Chap. 42
Regge calculus, variational principle for geometrodynamics 1170
Regge — Wheeler radial coordinate see “Tortoise coordinate”
Reissner — Nordstram geometry as limiting case of Kerr — Newman 878
Reissner — Nordstram geometry coordinates with infinity conformally transformed 920
Reissner — Nordstram geometry derivation of metric 840—841
Reissner — Nordstram geometry global structure of 920—921
Reissner — Nordstram geometry Kruskal-like coordinates for 841
Reissner — Nordstram geometry throat for Q = M identical to Bertoiti — Robinson universe 845
Reissner — Nordstram geometry uniqueness of (Birkhoff-iype theorem) 844ff
Relative acceleration see “Geodesic deviation”
Relativity see “Special relativity”; “General relativity”
Renormalization of zero-point energy of particles and fields 426ff
Retarded fields and radiation reaction 474
Retarded potential 121
Reversible and irreversible transformations in black-hole physics 889f
Ricci curvature see under “Curvature formalism
Ricci rotation 1-forms see «Rotation 1-forms”
Ricci rotation coefficients see “Connection coefficients”
Riemann see under “Curvature formalism
Riemann normal coordinates 285ff 480—486
Riemannian geometry characterized 242 304f
Riemannian geometry of apple, is locally Euclidean 19—21
Riemannian geometry of spacetime, is locally Lorentzian 19—23 (see also specific concepts such “Connection”)
Riemannian geometry Riemann’s founding of 220
Riemannian geometry track-1 treatment of Chap. 8
Riemannian geometry track-2 treatment of Chap. 13
Robertson — Walker line element 722 759
Rods 301 393 396—399
Roll — Krotkov — Dicke experiment see “Eotvos — Dicke experiments”
Rotation 1-forms 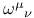 350—354 360 350—354 360
Rotation 1-forms 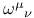 matrix notation for 359 (see also “Covariant derivative” “Connection matrix notation for 359 (see also “Covariant derivative” “Connection
Rotation as stabilizer of stars 633f
Rotation group SO(3), manifold of generators 242—243 264
Rotation group SO(3), manifold of geodesies and connection 264 332
Rotation group SO(3), manifold of isometric to 3-sphere 725
Rotation group SO(3), manifold of metric 332
Rotation group SO(3), manifold of Riemann curvature 288
Rotation group SO(3), manifold of structure constants 243 332
Rotation group SO(3), manifold of used in constructing mixmaster cosmological model 807
Rotation matrices see “Spin matrices”
Rotation of universe, limits on 939
Rotation operators see “Spin matrices”
Rotation rigid-body 123f
Rotations composition of 1135—1138
Rotations half-angles arise from reflections 1137
Rotations in coordinate plane 67
Rotations infinitesimal 170f 1140ff
Rotations represented as two reflections 1137ff
Rotations Rodrigues formula 1137
Rutherford scattering 647 669
Rutherford scattering relativistic corrections to 669f
Saddle points, number of 318
Sakharov view of gravitation 426—428
Scalar field equation of motion, from Einstein’s field equation 483
Scalar field propagation in Schwarzschild geometry 863 868ff
Scalar field stress-energy tensor 483
Scalar product of vectors 22 52f 62
Scalar-tensor theories of gravity see under “Gravitation theories
Schild’s argument for curvature 187—189
Schild’s ladder, applications 251—253 258 263 268 278
Schild’s ladder, described 249
Schwarzschild coordinates for a pulsating star 689
Schwarzschild coordinates for any static, spherical system 597
Schwarzschild coordinates for Schwareschild geometry 607
Schwarzschild coordinates pathology at gravitational radius 11 823—826
Schwarzschild geometry 822
Schwarzschild geometry applications as exterior of a collapsing star 846—850
Schwarzschild geometry applications as external field of a static star 607
Schwarzschild geometry applications many Schwarzschild solutions joined in lattice to form closed universe 739f
Schwarzschild geometry applications matched to Friedmann geometry to produce model for collapsing star 851ff
Schwarzschild geometry as limiting case of Kerr — Newman 878
Schwarzschild geometry BirkhofTs theorem for 843—844
Schwarzschild geometry coordinate systems and reference frames coordinates with infinity conformally transformed 919f
Schwarzschild geometry coordinate systems and reference frames ingoing Eddington — Finklestein coordinates 312 828f 849
Schwarzschild geometry coordinate systems and reference frames isotropic coordinates 840
Schwarzschild geometry coordinate systems and reference frames Kruskal — Szekeres coordinates 827 831—836
Schwarzschild geometry coordinate systems and reference frames Novikov coordinates 826—827
Schwarzschild geometry coordinate systems and reference frames orthonormal frames 821
Schwarzschild geometry coordinate systems and reference frames outgoing Eddington — Finklestein coordinates 829ff
Schwarzschild geometry coordinate systems and reference frames Schwarzschild coordinates 607 823—826
Schwarzschild geometry coordinate systems and reference frames tortoise coordinate 663 665f
Schwarzschild geometry derivation from full field equations 607
Schwarzschild geometry derivation from initial-value equation 538
Schwarzschild geometry destruction of all particles that fall inside gravitational radius 836 839 860—862
Schwarzschild geometry Dirac equation in 1164
Schwarzschild geometry explored by radially infalling observer 820—823
Schwarzschild geometry in extens Chaps 25 31
Schwarzschild geometry perturbations of high-frequency, analyzed by geometric optics 640
Schwarzschild geometry perturbations of stability against small 884
Schwarzschild geometry perturbations of wave equations for, related to Hamilton — Jacobi equation 640
Schwarzschild geometry photon motion in capture cross section 679
Schwarzschild geometry photon motion in critical impact parameter for capture 673
Schwarzschild geometry photon motion in effective potential for radial part of motion 673f 676
Schwarzschild geometry photon motion in escape versus capture as a function of propagation direction 675
Schwarzschild geometry photon motion in impact parameter 672
Schwarzschild geometry photon motion in qualitative description of 674f
Schwarzschild geometry photon motion in scattering cross section 676—679
Schwarzschild geometry photon motion in shape of orbit 673 677
Schwarzschild geometry Riemann curvature 821ff
Schwarzschild geometry Riemann curvature structure and evolution Einstein — Rosen bridge (wormhole) 837ff 842f
Schwarzschild geometry Riemann curvature structure and evolution evolution 838ff 842
| Schwarzschild geometry Riemann curvature structure and evolution not static inside gravitational radius 838
Schwarzschild geometry Riemann curvature structure and evolution Riemann curvature structure and evolution diagram of causal structure 920
Schwarzschild geometry Riemann curvature structure and evolution Riemann curvature structure and evolution embedding diagrams 528 837 839
Schwarzschild geometry Riemann curvature structure and evolution Riemann curvature structure and evolution singularities see “Singularities of Schwarzschild geometry”
Schwarzschild geometry Riemann curvature structure and evolution Riemann curvature structure and evolution singularities at r = 0 see under “Singularities”
Schwarzschild geometry Riemann curvature structure and evolution topology 838ff
Schwarzschild geometry test-particle motion in analyzed using Hamilton — Jacobi theory 649
Schwarzschild geometry test-particle motion in analyzed using symmetry-induced constants of the motion 656—672
Schwarzschild geometry test-particle motion in angular momentum 656ff
Schwarzschild geometry test-particle motion in binding energy of last stable circular orbit 885 911
Schwarzschild geometry test-particle motion in circular orbits, stability of 662
Schwarzschild geometry test-particle motion in conserved quantities for 656
Schwarzschild geometry test-particle motion in deflection angle 671
Schwarzschild geometry test-particle motion in effective potential for radial part of motion 639 656 659—662
Schwarzschild geometry test-particle motion in energy-at-infinity 656ff
Schwarzschild geometry test-particle motion in extensor Chap. 25
Schwarzschild geometry test-particle motion in nonradial orbits, details of 668
Schwarzschild geometry test-particle motion in orbit lies in a “plane” 645f 655
Schwarzschild geometry test-particle motion in periastron shift for nearly circular orbits 670
Schwarzschild geometry test-particle motion in qualitative description of orbits 662
Schwarzschild geometry test-particle motion in radial orbits, details of 663—668 820—823 824—826 835
Schwarzschild geometry test-particle motion in scattering cross section 669f
Schwarzschild geometry wave propagation in effective potentials for 868 870
Schwarzschild geometry wave propagation in electromagnetic field, Newman — Penrose constants 870f
Schwarzschild geometry wave propagation in fields of zero rest mass, integer spin 866
Schwarzschild geometry wave propagation in scalar field, analyzed in detail 863 868ff
Schwarzschild lattice universe 739f
Schwarzschild radius see “Gravitational radius”
Schwarzschild surface see “Gravitational radius”
Schwarzschild’s uniform-density stellar model 609—612
Second law of black-hole dynamics 931ff
Second law of black-hole dynamics formulated with assumptions ignored 889 891
Second law of black-hole dynamics reversible and irreversible transformations 889f 907—910 913
Second law of black-hole dynamics used to place limits on gravitational waves from hole-hole collisions 886
Second law of thermodynamics 563 567f
Second moment of mass distribution, defined 977
Second, changing definitions of 23—29
Selector parameter defined 265—266
Selector parameter used in analysis of geodesic deviation Chap. 11
Semicolon notation for covariant derivative 210
Semimajor axis of an elliptic orbit 647
Separation vector 29ff 218f 265—270
Shear stress idealized away for perfect fluid 140
Shear stress in PPN formalism 1074 1075n
Shear stress produced by viscosity 567
Shell crossing 859
Shift function as Lagrange multiplier 487
Shift function award of arbitrariness in, reversed 532
Shift function covariant and contravariant forms of 507f
Shift function metric interval as fixed by 507
Shift function two variational principles for 538
Shock waves hydrodynamic 559 564 628
Shock waves in spacetime curvature 554
Signals, extraction of from noise 1036—1038
Signature, of metric 311
Simple fluid, defined 558
simplex 307 38Of 1167ff
Simultaneity as term for spacelike slice see “Spacelike slice”
Simultaneity in Newion, Minkowskii, and Einstein spacetime 296
Singularities in geometry of spacetime and spherical gravitational collapse of a star 846 860ff
Singularities in geometry of spacetime cosmic censorship vs. naked singularities 937
Singularities in geometry of spacetime definitions of 934
Singularities in geometry of spacetime in Schwarzschild geometry, and evolution of the geometry 838f
Singularities in geometry of spacetime Mixmaster 805—813
Singularities in geometry of spacetime Mixmaster changing standards of time near 813f
Singularities in geometry of spacetime Mixmaster initial, of the universe 769f
Singularities in geometry of spacetime Mixmaster initial, of the universe prospects for understanding 707
Singularities in geometry of spacetime Mixmaster initial, of the universe what “preceded” it 769f
Singularities in geometry of spacetime Mixmaster is generic 806 940
Singularities in geometry of spacetime Mixmaster should one worry about singularities Misner’s viewpoint 813f
Singularities in geometry of spacetime Mixmaster should one worry about singularities Thome’s neutrality 1010f
Singularities in geometry of spacetime Mixmaster should one worry about singularities Wheeler’s viewpoint 1196ff
Singularities in geometry of spacetime Mixmaster unphysical, due to overidealization shell crossings 859
Singularities in geometry of spacetime Mixmaster unphysical, due to overidealization surface layers 552—556
Singularities in geometry of spacetime remote possibility that infalling objects might destroy 840
Singularities in geometry of spacetime structures of 935 940 804ff
Singularities in geometry of spacetime theorems on creation of 934ff 936 938 762
Singularities, coordinate 10—12
Singularities, coordinate illustrated by Schwarzschild coordinates 11 823ff
Size of accelerated frame 168f
Size related to angular momentum 162
Skeleton geometry 309 1169
Skeleton history 499
Slicing of spacetime 506 (see also “Spacelike slice”)
Solar system 752—756
Solar system ephemeris for (J.P.L.) 1095 1097
Solar system Nordtvedt effect in 1128 (see also “Earth” “Moon” “Planetary “Sun” “Experimental
Solar system relativistic effects in, magnitude of 1048 1068
Source counts in cosmology 798
Space foamlike structure and quantum fluctuations 1204
Space Newtonian absolute 19 40 291f
Space not spacetime, as the dynamic object 1181 (see also “Manifold” Differential “Differential “Affine “Riemannian
Space theory of matter 1202—1205
Spacecraft, used to test general relativity 1108f 1114
Spacelike slice as the dynamic object in superspace 423f 1181
Spacelike slice as “moment of time’ in spacetime 713f
Spacelike slice geometrodynamics and electrodynamics derived from physics on 419—423 (see also “Embedding diagrams” “Initial “Three-geometries”
Spacetime geometry Ensteinian as classical approximation 1181f
Spacetime geometry Ensteinian as classical leaf slicing through superspace 1184 (see also “General Relativity” “Geometrodynamics” “Curvature
Spacetime geometry Ensteinian as dynamic participant in physics 337
Spacetime geometry Ensteinian curvature of implied by gravitational red shift 187ff
Spacetime geometry Ensteinian modeled by apple, 4 Riemannian character tested by stability of Earth 398f
Spacetime geometry Ensteinian response to matter, as heart of general relativity 404
Spacetime geometry Ensteinian stratification denied by locally Lorentz character of physics 304f
Spacetime geometry Ensteinian viewed as a “gravitational field” 399f
Spacetime geometry Minkowskiian (Loreniz) see «Lorentz geometry”
Spacetime geometry Newtonian see “Newton — Cartan theory of gravity”
Spacetime geometry Newtonian, Minkowskiian and Einsteinian, compared and contrasted 296 437
Special relativity briefly outlined 47—48
Special relativity does not take in gravitation Chap. 7
Special relativity local validity as central feature of curved spacetime 304f (see also specific concepts e.g. “Electromagnetic “Lorentz
Special relativity spelled out Chaps. 2—6
Specific flux, defined 1025
Specific intensity, denned 587 589
Sphere 2-dimensional 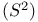 metric on 340 metric on 340
Sphere 2-dimensional 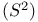 Riemann tensor of 341 Riemann tensor of 341
Sphere 2-dimensional 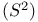 topology of 241f topology of 241f
Sphere 2-dimensional 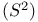 two coordinate patches to cover 12 two coordinate patches to cover 12
Sphere 3-dimensional 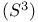 compared with spheres of lower dimensionality 704 compared with spheres of lower dimensionality 704
Sphere 3-dimensional 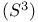 embedding diagram 723 embedding diagram 723
Sphere 3-dimensional 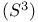 hyperspherical coordinates and metric for 723f hyperspherical coordinates and metric for 723f
Sphere 3-dimensional 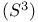 isometric to manifold of rotation group 725 isometric to manifold of rotation group 725
Sphere 3-dimensional 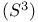 Riemann curvature tensor 721 Riemann curvature tensor 721
Sphere 3-dimensional 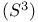 volume of 724 volume of 724
Spherical symmetry, Killing vectors for 658
Spherical systems, dynamic Birkhoff’s theorem for 883f
Spherical systems, dynamic curvature tensors for 361f
Spherical systems, dynamic Schwarzschild coordinates for 616f 689
Spherical systems, static curvature tensors for 360f
Spherical systems, static isotropic coordinates for 595
Spherical systems, static orthonormal frames for 598
Spherical systems, static rigorous derivation of line element 616f
Spherical systems, static Schwarzschild coordinates for 594—597
Spin matrices algebraic properties 1137—1142
Spin matrices and 3-vectors 1140f
Spin matrices and 4-vectors 1142f
Spin matrices as quaternions or rotation operators 1136
Spin matrices associated spin matrices 1152f
Spin matrices Hermitian conjugate of 1138
Spin matrices in law of combination of rotations 1136
Spin matrices multiplication law for 1153
Spin, as nonclassical two-valuedness 1204
Spindown of black holes 886
Spinning body equation of motion for 1120f
Spinning body spin precessions due to space curvature (“geodetic’) 1119f
Spinning body spin precessions frame-dragging 1119f
Spinning body spin precessions Thomas 175f 1118 1145ff
Spinning body spin precessions “general” 391f
Spinning body transport law for spin Fermi — Walker, in absence of curvature coupling 165 176f 1117
Spinning body transport law for spin modified by curvature coupling 391f
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



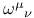
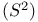 metric on
metric on 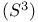 compared with spheres of lower dimensionality
compared with spheres of lower dimensionality