|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Misner C.W., Thorne K.S., Wheeler J.A. — Gravitation |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Gravitational waves generation by slow-motion, weak-field sources, formulas specialized to impulse events 987
Gravitational waves generation by slow-motion, weak-field sources, nonexistence of monopole and dipole waves 974—978
Gravitational waves generation by slow-motion, weak-field sources, order-of-magnitude formulas for 978—979 980—981
Gravitational waves generation by slow-motion, weak-field sources, role of “gravitational stresses” in generation 996—998
Gravitational waves generation by slow-motion, weak-field sources, waves are predominantly quadrupolar 975—978
Gravitational waves generation by strong-field sources, techniques for calculating particle falling into black hole, by perturbations of Schwarzschild metric 982 983
Gravitational waves generation by strong-field sources, techniques for calculating, rotation of a deformed relativistic star, by perturbations of spherical stellar structure 986
Gravitational waves generation by strong-field sources, techniques for calculating, vibrations of a relativistic star, by perturbations of equilibrium stellar structure 984—985
Gravitational waves initial-value solutions for 536
Gravitational waves intensity and spectrum of waves that bathe Earth, estimate of 986
Gravitational waves linearized theory of Fourier analysis of 1026 1027
Gravitational waves linearized theory of gauge transformations that maintain Lorentz gauge 945
Gravitational waves linearized theory of geodesic deviation 950—955 1011—1012
Gravitational waves linearized theory of in extenso 944—955
Gravitational waves linearized theory of Lorentz gauge condition 944—945
Gravitational waves linearized theory of methods to calculate transverse-traceless part 948—949
Gravitational waves linearized theory of plane-wave solutions 945—946 949 1004—1005
Gravitational waves linearized theory of polarization 952—955
Gravitational waves linearized theory of propagation equation 945
Gravitational waves linearized theory of relative accelerations are purely transverse 951
Gravitational waves linearized theory of Riemann tensor 948
Gravitational waves linearized theory of specific flux of 1027
Gravitational waves linearized theory of transverse-traceless gauge 946—950
Gravitational waves monopole and dipole waves absolutely forbidden 977 978
Gravitational waves nonlinear interaction of waves with themselves nonexistence of precisely periodic waves 956
Gravitational waves nonlinear interaction of waves with themselves self-gravitational attraction 957 968
Gravitational waves nonlinear interaction of waves with themselves wave-wave scattering 968
Gravitational waves propagation through curved spacetime analogy with water waves on ocean 993—994
Gravitational waves propagation through curved spacetime backscatter off curvature 957 864—865 869—871
Gravitational waves propagation through curved spacetime geometric optics formalism 971—972
Gravitational waves propagation through curved spacetime gravitational redshift of frequency 956—957 968
Gravitational waves propagation through curved spacetime propagation equation 967—968
Gravitational waves propagation through curved spacetime propagation of polarization tensor 968 971
Gravitational waves propagation through curved spacetime refraction of wave fronts (deflection of rays) by background curvature 956 968 972
Gravitational waves propagation through curved spacetime shock fronts 554
Gravitational waves propagation through curved spacetime shortwave formalism for 964—973 (see also “Gravitational waves: shortwave formalism”)
Gravitational waves propagation through curved spacetime spinor formalism for 1165 (see also “Gravitational waves: nonlinear interaction of waves with themselves”)
Gravitational waves propagation through curved spacetime stress-energy tensor 969—970 (see also “Gravitational waves: stress-energy tensor for”
Gravitational waves propagation through curved spacetime tails due to interaction with background curvature 957 864—865 869—871
Gravitational waves radiation reaction damping of neutron-star vibrations by 620 628 984f
Gravitational waves radiation reaction evolution of binary-star orbits due to 988
Gravitational waves radiation reaction forbids existence of exactly periodic waves 956
Gravitational waves radiation reaction formalism for calculating, in wreak-field, slow-motion sources 993ff 1001ff
Gravitational waves radiation reaction linked to outgoing-wave condition 993 1001—1002
Gravitational waves radiation reaction order-of-magnitude formulas for 979 981
Gravitational waves shortwave formalism assumptions underlying 964
Gravitational waves shortwave formalism Brill-Hartle averaging process 970
Gravitational waves shortwave formalism coarse-grain viewpoint vs. fine-grain viewpoint 965
Gravitational waves shortwave formalism expansion of Ricci tensor 964—965
Gravitational waves shortwave formalism expansion parameters of 964
Gravitational waves shortwave formalism gauge freedom 967—969
Gravitational waves shortwave formalism geometric optics specialization 971—972
Gravitational waves shortwave formalism Lorentz gauge 968
Gravitational waves shortwave formalism propagation equation 967—968
Gravitational waves shortwave formalism stress-energy tensor 969—970 (see also “Gravitational waves: stress-energy tensor”)
Gravitational waves shortwave formalism transverse-traceless gauge 969
Gravitational waves shortwave formalism variational principle used to derive 972—973
Gravitational waves shortwave formalism “steady” coordinates 964
Gravitational waves sources of astrophysical sources, order-of-magnitude formulas for 980—981
Gravitational waves sources of atomic bomb 987
Gravitational waves sources of big-bang origin of universe 712 736—737 764—765
Gravitational waves sources of binary stars 986 988—990 995
Gravitational waves sources of collapses and explosions in Virgo cluster of galaxies 1042
Gravitational waves sources of collision and coalescence of black holes 886 939 982
Gravitational waves sources of explosion of a star 987
Gravitational waves sources of fall of matter into a black hole 885 982 983 986
Gravitational waves sources of fission of an atomic nucleus 987
Gravitational waves sources of gravitational collapse of a star 628 629 1041
Gravitational waves sources of meteorite striking earth 987
Gravitational waves sources of rotating steel beam 979—980
Gravitational waves sources of rotation of a deformed neutron star (young pulsar) 628f 983 986 1040
Gravitational waves sources of supernova explosions 982 1040 1042
Gravitational waves sources of vibrations of a black hole 886
Gravitational waves sources of vibrations of neutron star 982—986
Gravitational waves stress-energy tensor for as source for background curvature of spacetime 966 973
Gravitational waves stress-energy tensor for divergence vanishes 970
Gravitational waves stress-energy tensor for elementary summary of 955—956
Gravitational waves stress-energy tensor for expressed as an average of stress-energy pseudotensor 972
Gravitational waves stress-energy tensor for expressed in terms of metric perturbations 969
Gravitational waves stress-energy tensor for expression for in traceless Lorentz gauge 970
Gravitational waves stress-energy tensor for for exact plane wave 963
Gravitational waves stress-energy tensor for for geometric-optics waves 972
Gravitational waves stress-energy tensor for for waves in nearly flat spacetime 955—956
Gravitational waves stress-energy tensor for gauge invariance of 972
Gravitational-wave cross sections for a Weber bar 1025
Gravitational-wave cross sections for a Weber bar in multimode operation 1035
Gravitational-wave cross sections for any resonant, mechanical detector 1025 1029 1032
Gravitational-wave cross sections for Earth in fundamental quadrupole mode 1036
Gravitational-wave cross sections for idealized vibrator 1024 1025
Gravitational-wave cross sections limits on usefulness of concept of cross section 1019 1022
Gravitational-wave cross sections related to emission patterns 1032—1033 1035
Gravitational-wave cross sections summary of ways to use. for wave-dominated detectors 1020— 1021
Gravitational-wave cross sections use of for noisy detectors 1038—1039
Gravitational-wave cross sections used to calculate total energy deposited in detector 1027 1028
Gravitational-wave detailed analysis of any resonant vibrator, analyzed by detailed balance 1030 1033
Gravitational-wave detailed analysis of any resonant vibrator, analyzed by dynamic method 1031—1034
Gravitational-wave detailed analysis of Earth vibrating in quadrupole mode 1035—1036
Gravitational-wave detailed analysis of electromagnetic waves in a toroidal wave guide 1043—1044
Gravitational-wave detailed analysis of idealized vibrator (two masses on a spring) 1022—1028
Gravitational-wave detailed analysis of noisy resonant vibrator (extraction of signal from noise) 1036—1040
Gravitational-wave detailed analysis of two freely falling bodies 1018
Gravitational-wave detectors conceivable types of angular accelerations of driven oscillators 1013 1017
Gravitational-wave detectors conceivable types of angular accelerations of rotating bars (“heterodyne detector”) 1013 1016—1017
Gravitational-wave detectors conceivable types of beads on stick 444f
Gravitational-wave detectors conceivable types of Earth-moon separation 1013 1014 1018
Gravitational-wave detectors conceivable types of electromagnetic waves in a toroidal wave guide 1043—1044
Gravitational-wave detectors conceivable types of idealized vibrator (2 masses on a spring) 1022—1028
Gravitational-wave detectors conceivable types of nonmechanical detectors 1040
Gravitational-wave detectors conceivable types of normal-mode vibrations of an elastic bar 1013 1016 1025 1035 1038
Gravitational-wave detectors conceivable types of normal-mode vibrations of Earth and moon 1013 1015
Gravitational-wave detectors conceivable types of normal-mode vibrations of general elastic bodies 1013 1016 1025 1028—1035 1041—1042
Gravitational-wave detectors conceivable types of oscillations of Earth’s crust 1013 1015
Gravitational-wave detectors conceivable types of pumping of fluid in a rotating pipe 1013 1018
Gravitational-wave detectors methods of analyzing (for mechanical detectors small compared to wavelength) driving forces of waves 1006 1009 1010
Gravitational-wave detectors methods of analyzing (for mechanical detectors small compared to wavelength) dynamic analysis: Newtonian equation of motion plus wave driving forces 1006—1009
Gravitational-wave detectors methods of analyzing (for mechanical detectors small compared to wavelength) for noisy detector 1019 1036—1040
Gravitational-wave detectors methods of analyzing (for mechanical detectors small compared to wavelength) line-of-force diagram 1011—1012
Gravitational-wave detectors methods of analyzing (for mechanical detectors small compared to wavelength) method of detailed balance 1028 1029—1030 1033
Gravitational-wave detectors methods of analyzing (for mechanical detectors small compared to wavelength) proper reference frame of detector 1005—1006 1010 1012
Gravitational-wave prospects for the future 1040ff
Gravitational-wave sensors for monitoring displacements 1041 1042
Gravitational-wave thermally noisy detectors extraction of small signal from noise 1036—1040
Gravitational-wave thermally noisy detectors sensitivity of to hammer-blow waves 1039
Gravitational-wave thermally noisy detectors ways to improve sensitivity 1040
Gravitons 972
Gravity gradiometer 400—403
Group see “Rotation group”; “Lorentz group”
Group of motions 652—653 (see also “Killing vector fields”)
Gyromagnetic ratio, of Kerr — Newman black hole 883 892
Gyroscopes employed in constructing proper reference frame 327 330f
Gyroscopes employed in definition of Fermi — Walker transport 165
Gyroscopes precession of as experimental test of general relativity 1117—1120 (see also “Dragging of inertial frames”)
Hair on a billiard ball 978
Hair on a hole see «Kerr — Newman geometry uniqueness
Hamilton — Jacobi theory 486ff 641—649
Hamilton — Jacobi theory, for electrodynamics 1195
Hamilton — Jacobi theory, for free particle 1194
Hamilton — Jacobi theory, for geometrodynamics in superspace 423f 1180—1190
Hamilton — Jacobi theory, for harmonic oscillator 1194
Hamilton — Jacobi theory, for test-particle motion deflection of light by sun, in PPN formalism 1102f
Hamilton — Jacobi theory, for test-particle motion in Kerr — Newman gravitational and electromagnetic fields 900—901
Hamilton — Jacobi theory, for test-particle motion in Newtonian M/r potential 644—649
Hamilton — Jacobi theory, for test-particle motion in Schwarzschild gravitational field 649
Hamilton — Jacobi theory, for test-particle motion perihelion shift in PPN formalism 1114f
Hamilton — Jacobi theory, relation to quantum theory 641—643
Hamiltonian contrasted with super-Hamiltonian, for charged particle in field 488—489
Hamiltonian dynamics, in the language of forms 125—126
Hamiltonian dynamics, symplectic structure of 126
Hamiltonian electromagnetic 497
Hamiltonian for test-particle in Newtonian l/r potential 644 (see also “Super-Hamiltonian”)
| Hamiltonian, ADM, applied to mixmaster cosmology 809
Hamilton’s principle for geodesic motion 654
Harrison — Wakano — Wheeler stellar models 625ff 696
Harrison — Wheeler equation of state 625
Hat product see “Wedge product”
Heat flow in general relativity heat-flux 4-vector 567
Heat flow in general relativity in a stationary gravitational field 568
Heat flow in general relativity law of thermal conductivity 567
Heat flow in general relativity references on 559
HII regions in galaxies 710 761 786f
Hilbert’s variational principle see “Variational principle Hilbert’s”
Histories, democracy of 320
Histories, space of 318—319
Histories, sum over 320 419 499f
Holonomic basis 204 210 239
Homologous pulsations of a star 697 1079
Honeycomb structure see “Forms”
Horizons in cosmology 815f
Horizons in Friedmann cosmologies 740ff 815
Horizons, in black-hole physics caustics of 925
Horizons, in black-hole physics created by gravitational collapse 862 863 867 924
Horizons, in black-hole physics definition of 923—924
Horizons, in black-hole physics for Kerr — Newman geometry 879ff
Horizons, in black-hole physics for Kerr — Newman geometry angular velocity of 914
Horizons, in black-hole physics for Kerr — Newman geometry area of 889 914
Horizons, in black-hole physics for Kerr — Newman geometry generators of 903f
Horizons, in black-hole physics generators of 903—904 925 929—931 932
Horizons, in black-hole physics global structure analyzed 926—931
Horizons, in black-hole physics global structure of (theorem) 924—925
Hubble expansion rate 709f
Hubble expansion rate distance-redshift relation used in measuring 780—781
Hubble expansion rate expressed in terms of expansion factor a (t) 732
Hubble expansion rate relationship to other cosmological parameters 771—773 (see also under “Cosmological models”
Hubble expansion rate, history of knowledge of 709—710 758—761
Hughes — Drever experiment 1064
Hydrodynamics equilibrium in a stationary gravitational field 566 568
Hydrodynamics Euler equation 564
Hydrodynamics for a fluid with viscosity and heat flow 567—568
Hydrodynamics for a simple fluid with no heat flow or viscosity 562—563
Hydrodynamics general relativistic basic references 562n 568
Hydrodynamics gradient of 4-velocity resolved into 4-acceleration. expansion, relation. and shear 566
Hydrodynamics interaction of charged matter with an electromagnetic field 570 (see also “Thermodynamics laws
Hydrodynamics Newtonian, in absence of gravity 152ff
Hydrodynamics Newtonian, in presence of gravity 387f 1077—1080
Hydrodynamics post-Newtonian see under “PPN formalism”
Hydrodynamics volume changes related to divergence of flow lines 565
Hydrostatic equilibrium buoyant force 606
Hydrostatic equilibrium in any stationary gravitational field 566
Hydrostatic equilibrium in static, spherical star 601—602 605
Hydrostatic equilibrium Oppenheimer — Volkoff equation of 605
Hyperbolic motion of an accelerated observer 166ff 173f
Hypersurface, spacelike see «Spacelike slice”
Ideal gas 139f
Identity, as automatically fulfilled conservation law 405
Imaginary time coordinate not used 51
Impact parameter for hyperbolic orbit in Schwarzschild field 670
Impact parameter for hyperbolic, Newtonian orbit 647
Impact parameter for photon in PPN formalism 1101f
Impact parameter for photon in Schwarzschild field 672
Index manipulations in affine manifolds 225f
Index manipulations in curved, Riemannian manifolds. 201—204 223f
Index manipulations in global Lorentz frames 85
Index manipulations in linearized theory 436
Index, contravariant and covariant 76
Induction, from electromagnetic 4-potential 122
Inertia 460
Inertial forces 165 332
Inertial forces in Newton — Cartan theory 294
Inertial frames, dragging of see «Dragging of inertial frames”
Inertial guidance 247
Inertial mass 159f 431 1051
Inertial reference frame, local (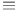 local Lorentz frame if orthonormal coordinates are used) 18f local Lorentz frame if orthonormal coordinates are used) 18f
Inertial reference frame, local (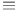 local Lorentz frame if orthonormal coordinates are used) defined by uniform velocity of free test particles 23 local Lorentz frame if orthonormal coordinates are used) defined by uniform velocity of free test particles 23
Inertial reference frame, local (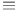 local Lorentz frame if orthonormal coordinates are used) mathematical representation of see “Ricmann normal coordinates” “Lorentz local” local Lorentz frame if orthonormal coordinates are used) mathematical representation of see “Ricmann normal coordinates” “Lorentz local”
Inertial reference frame, local (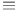 local Lorentz frame if orthonormal coordinates are used) used in analysis of tide-producing acceleration 29—37 local Lorentz frame if orthonormal coordinates are used) used in analysis of tide-producing acceleration 29—37
Infinitesimal Lorentz transformation see “Lorentz transformation infinitesintal”
Infinity, regions of in asymptotically flat spacetime 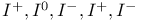 detined 917—918 detined 917—918
Infinity, regions of in asymptotically flat spacetime conformal transformations of 919—921 936
Infinity, regions of in asymptotically flat spacetime conformally transformed coordinate diagrams 919—921
Initial-value data as uniquely determining future, Hilbert on 434
Initial-value data for geometrodynamics compatible on spacelike slice 489—490
Initial-value data for geometrodynamics count of 529—533
Initial-value data for geometrodynamics improperly posed data 534—535
Initial-value data for geometrodynamics in extensor Chap. 21
Initial-value data for geometrodynamics on characteristic surface 490
Initial-value data for geometrodynamics required for dynamics 484—485
Initial-value data for geometrodynamics separation of time and dynamic data 533
Initial-value data for geometrodynamics thin-sandwich conjecture 534
Initial-value data for geometrodynamics time and dynamic data mixed in 3-geometry 533
Initial-value data for geometrodynamics York’s formulation of gives conformal 3-geometry 540—541
Initial-value data for geometrodynamics York’s formulation of gives conjugate York momenta 542
Initial-value data for geometrodynamics York’s formulation of gives York’s curvature 541
Initial-value data for geometrodynamics York’s formulation of on hypersurface of zero or constant extrinsic time 539—540
Initial-value data for geometrodynamics York’s formulation of sketched 490
Initial-value data formulation of on characteristic hypersurface 554
Initial-value data mystery of what fixes them 555
Initial-value equations for geometrodynamics 515—516 519 525 531—535
Initial-value problem for geometrodynamics other symmetric cases as route to cosmology 537 (see also “Geometrodynamics” “Integrating
Initial-value problem for geometrodynamics other symmetric cases Friedmann universe 537 705f 727f 744
Initial-value problem for geometrodynamics other symmetric cases mixmaster universe 537 806—811
Initial-value problem for geometrodynamics other symmetric cases pulsating star 691—694
Initial-value problem for geometrodynamics other symmetric cases waves with cylindrical symmetry 537
Initial-value problem for geometrodynamics other symmetric cases waves with spherical symmetry 537
Initial-value problem for geometrodynamics thin-sandwich formulation of as guide in counting degrees of freedom 529—533
Initial-value problem for geometrodynamics thin-sandwich formulation of as guide to geometrodynamics 529—531
Initial-value problem for geometrodynamics thin-sandwich formulation of as option in specifying data 529
Initial-value problem for geometrodynamics thin-sandwich formulation of electrodynamic analog 529
Initial-value problem for geometrodynamics time-antisymmetric case 490
Initial-value problem for geometrodynamics time-antisymmetric case formulated 536
Initial-value problem for geometrodynamics time-antisymmetric case mass of wave is positive 536
Initial-value problem for geometrodynamics time-antisymmetric case wave equation for conformal correction factor 536
Initial-value problem for geometrodynamics time-symmetric case 490
Initial-value problem for geometrodynamics time-symmetric case formulated 535
Initial-value problem for geometrodynamics time-symmetric case gravitational wave amplitude in 536
Initial-value problem for geometrodynamics time-symmetric case role of base metric in 535
Initial-value problem for geometrodynamics time-symmetric case wave equation for conformal correction factor 535
Initial-value problem for geometrodynamics York’s formulation of existence and uniqueness of solutions 543
Initial-value problem for geometrodynamics York’s formulation of wave equation for conformal factor 542
Initial-value theory for electrodynamics 523f 526 529ff “Integrating
Injection energy 561 562
Integral conservation law 146
Integrating forward in time geometrodynamic equation compared to electrodynamics 527—528
Integrating forward in time geometrodynamic equation options in choice of lapse and shift 527—528
Integrating forward in time geometrodynamic equation statement of initial data in 526—527
Integrating forward in time Maxwell’s equations as guide to geometrodynamics 527 (see also “Electrodynamics” “Geometrodynamics” “Initial
Integrating forward in time Maxwell’s equations options in choice of potential 527
Integrating forward in time Maxwell’s equations statement of initial data in 527
Integration of differential forms 94—97 150f
Integration of tensors, in track-1 language 147ff (see also “Stokes’ theorem” “Gauss’s “Volume”)
Interference, constructive and destructive 419 423f 1185—1187
Interferometry, used to measure deflection of radio waves by sun 1104—1105
Intergalactic matter, mean density of 712 761f
Interval, Lorentz 19—23
Intrinsic curvature see under “Curvature formalism
Intrinsic time of Sharp, Baierlein, and Wheeler 487 490
Invariants of electromagnetic field 110 480—483
Invariants of Riemann tensor 491
Irreducible mass of a black hole 889f 913
Isolated system 454
Isometry 652—653 (see also “Killing vector fields”)
Isostasy 402
Isothermal star clusters 685ff
Isotropic coordinates for a star 595
Isotropic coordinates for Schwarzschild geometry 840
Isotropic coordinates in post-Newtonian approximation 1097
Isotropy and homogeneity of universe adiabatic cooling of anisotropy 802
Isotropy and homogeneity of universe in extensor Chap 30
Isotropy and homogeneity of universe man could not exist in an anisotropic universe 939
Isotropy and homogeneity of universe pair creation by anisotropy energy 769 803—804
Isotropy and homogeneity of universe viscous dissipation of anisotropy 769 802—803
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



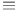 local Lorentz frame if orthonormal coordinates are used)
local Lorentz frame if orthonormal coordinates are used) 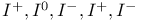 detined
detined