|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Misner C.W., Thorne K.S., Wheeler J.A. — Gravitation |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Isotropy implies homogeneity 715 723
Jacobi identity, for commutators 240
Jacobian 93 148 160f
Jacob’s ladder see “Schild’s ladder”
Jeans instability 757
Junction conditions 490
Junction conditions across null surface 554
Junction conditions and motion of surface layer 555
Junction conditions applied to collapsing shell of dust 555—556
Junction conditions applied to surface of a collapsing star 852—853
Junction conditions extrinsic curvature may jump 554
Junction conditions from electrodynamics as guide 551
Junction conditions intrinsic geometry continuous 553
Junction conditions relevant components of Einstein field equation 552
Junction conditions surface stress-energy tensor 552—553
Jupiter, motion of satellites 637
Kasner cosmological model 801 805ff
Keplerian orbits in Newtonian field of a point mass 647—649
Keplerian orbits in Newtonian field of a point mass analyzed using Hamilton — Jacobi theory 644—649
Keplerian orbits in Newtonian field of a point mass effective potential for 661
Kepler’s laws, discovery by Kepler 755
Kepler’s laws, “1-2-3” law 39 450 457
Kernel, of wave operator 121
Kerr coordinates 879f
Kerr diagram 881
Kerr geometry, as limiting case of Kerr — Newman 878
Kerr — Newman geometry and electromagnetic field Boyer — Lindquist coordinates electromagnetic field tensor 877 878
Kerr — Newman geometry and electromagnetic field Boyer — Lindquist coordinates metric 877 878
Kerr — Newman geometry and electromagnetic field Boyer — Lindquist coordinates pathology of at horizon 880
Kerr — Newman geometry and electromagnetic field Boyer — Lindquist coordinates vector potential 898
Kerr — Newman geometry and electromagnetic field dynamic properties change of M, Q, S when particles fall into horizon 904—910 913
Kerr — Newman geometry and electromagnetic field dynamic properties electromagnetic energy of 890
Kerr — Newman geometry and electromagnetic field dynamic properties irreducible mass 889—890 913
Kerr — Newman geometry and electromagnetic field dynamic properties reversible and irreversible transformations of 889—890
Kerr — Newman geometry and electromagnetic field dynamic properties role as endpoint of gravitational collapse 882—883
Kerr — Newman geometry and electromagnetic field dynamic properties rotational energy of 890
Kerr — Newman geometry and electromagnetic field dynamic properties stability against small perturbations 884—885
Kerr — Newman geometry and electromagnetic field history of 877n
Kerr — Newman geometry and electromagnetic field horizon 879ff
Kerr — Newman geometry and electromagnetic field horizon angular velocity of 914
Kerr — Newman geometry and electromagnetic field horizon area of 889 914
Kerr — Newman geometry and electromagnetic field horizon null generators of 903—904
Kerr — Newman geometry and electromagnetic field Kerr coordinates electromagnetic field tensor 879
Kerr — Newman geometry and electromagnetic field Kerr coordinates metric 879
Kerr — Newman geometry and electromagnetic field Kerr coordinates transformation between Kerr and Boyer — Lindquist coordinates 879f
Kerr — Newman geometry and electromagnetic field Kerr diagram for 881
Kerr — Newman geometry and electromagnetic field Kerr — Schild coordinates 903
Kerr — Newman geometry and electromagnetic field Killing tensor 893
Kerr — Newman geometry and electromagnetic field Killing tensor principal null congruences 901—904
Kerr — Newman geometry and electromagnetic field Killing vectors 879 892ff
Kerr — Newman geometry and electromagnetic field light cones 891 896—897
Kerr — Newman geometry and electromagnetic field light cones electromagnetic-field structure 877ff 883 892
Kerr — Newman geometry and electromagnetic field limiting cases (Schwarzschild, Reissner — Nordstram, Kerr, extreme Kerr — Newman) 878
Kerr — Newman geometry and electromagnetic field locally nonrotating observers 895—896
Kerr — Newman geometry and electromagnetic field magnetic dipole moment 883 892
Kerr — Newman geometry and electromagnetic field maximal analytic extension of 882
Kerr — Newman geometry and electromagnetic field multipole moments of 883 892
Kerr — Newman geometry and electromagnetic field parameters of (M, Q, S, or a) 878
Kerr — Newman geometry and electromagnetic field rotational properties dragging of inertial frames 879ff 893—896
Kerr — Newman geometry and electromagnetic field rotational properties ergosphere 880
Kerr — Newman geometry and electromagnetic field rotational properties gyromagnetic ratio 883 892
Kerr — Newman geometry and electromagnetic field rotational properties intrinsic angular momentum vector 891
Kerr — Newman geometry and electromagnetic field rotational properties static limit 879ff 894
Kerr — Newman geometry and electromagnetic field stationary observers 893—894
Kerr — Newman geometry and electromagnetic field test-particle motion in axial component of angular momentum 898—899
Kerr — Newman geometry and electromagnetic field test-particle motion in binding energy of last stable circular orbit 885 911
Kerr — Newman geometry and electromagnetic field test-particle motion in Carter’s fourth constant of the motion, 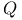 or or 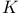 899 899
Kerr — Newman geometry and electromagnetic field test-particle motion in effective potential for equatorial motion 911
Kerr — Newman geometry and electromagnetic field test-particle motion in energy-at-inflnity 898—899 910
Kerr — Newman geometry and electromagnetic field test-particle motion in equations of motion in separated form 899—900 901
Kerr — Newman geometry and electromagnetic field test-particle motion in Hamilton — Jacobi derivation of equations of motion 900—901
Kerr — Newman geometry and electromagnetic field test-particle motion in orbits in equatorial plane 911—912
Kerr — Newman geometry and electromagnetic field test-particle motion in rest-mass of particle 899
Kerr — Newman geometry and electromagnetic field test-particle motion in super-Hamiltonian for 897
Kerr — Newman geometry and electromagnetic field uniqueness as external field of a black hole heuristic explanation of uniqueness 875 877
Kerr — Newman geometry and electromagnetic field uniqueness as external field of a black hole implications for realistic gravitational collapse 863
Kerr — Newman geometry and electromagnetic field uniqueness as external field of a black hole theorems implying uniqueness 876 938 939
Kerr — Newman geometry and electromagnetic field wave propagation in 914—915
Kerr — Schild coordinates 903
Killing tensor field 893n
Killing vector fields 650—653
Killing vector fields associated conservation laws for test-particle motion 651
Killing vector fields commutator of is Killing vector 654
Killing vector fields eigenvalue problem for finding 654
Killing vector fields for flat spacetime 654
Killing vector fields for Kerr — Newman geometry 879 892ff
Killing vector fields for spherically symmetric manifolds 658
Killing’s equation 650
Kinetic theory in curved spacetime applications 583
Kinetic theory in curved spacetime applications computation of optical appearance of a collapsing star 850
Kinetic theory in curved spacetime applications elementary expression for pressure 139—140
Kinetic theory in curved spacetime applications photons 587ff
Kinetic theory in curved spacetime applications relativistic star clusters 679—687
Kinetic theory in curved spacetime applications stress-energy tensor as integral over momentum Kinetic theory in curved spacetime applications space 589f
Kinetic theory in curved spacetime basic concepts distribution function (number density in phase space) defined 583f 590
Kinetic theory in curved spacetime basic concepts mass hyperboloid 585
Kinetic theory in curved spacetime basic concepts momentum space 583ff 590
Kinetic theory in curved spacetime basic concepts phase space 584f 590
Kinetic theory in curved spacetime basic concepts volume in phase space 584—587 590
Kinetic theory in curved spacetime basic laws collisionless Boltzmann equation (kinetic equation) 587 590
Kinetic theory in curved spacetime basic laws Liouville’s theorem for noninteracting particles in curved spacetime 584 586—587 590
Kinetic theory in curved spacetime basic laws specialized to photons 587—589
Kinetic theory in curved spacetime in extenso 583—590
Klein — Alfven cosmology 748 770
Kronecker delta 22
Kruskal diagrams 528 834f 839 848 855
Kruskal — Szekeres coordinates for metric in 827
Kruskal — Szekeres coordinates for relationship to Schwarzschild coordinates 833—835
Kruskal — Szekeres coordinates for Schwarzschild geometry 828—832
K’ai-feng observatory 11
Lagrangian perturbations 690—691
Lamb — Retherford shift, principal mechanism 1190
Landau — Lifshitz pseudotensor see “Pseudotensor”
Laplace operator, vs. d’Alembertian 177
Lapse function as Lagrange multiplier 487
Lapse function award of arbitrariness in, reversed 532
Lapse function covariant and contra variant forms of 507—508
Lapse function metric interval as fixed by 507
Lapse function variational principle for 538
Laser ranging to moon 1048 1130f
Lattice see “Clocks”; “Rods”
Laws of physics in curved spacetime 384—393 (see also specific laws e.g. “Kinetic “Hydrodynamics” “Conservation
Leap second 28
Least action, principle of applied in elementary Hamiltonian mechanics 125—126
Least action, principle of related to extremal time 315—324
Lens effect 589 795f 887
Levi — Civita tensor in flat spacetime 87f
Levi — Civita tensor in general basis 202 207
Levi — Civita tensor in spherical coordinates 206
Levi — Civita tensor orientation of 87f
Lie derivative independent of any affine connection 517
Lie derivative of a tensor 517
Lie derivative of a vector 240
Lie groups 198
Lie transport law 240
Light cone characterization of advanced and retarded potentials 122
Light cone Newton — Cartan vs. Einstein difference 297 (see also “Causal relationships”)
Light, bending of see “Deflection of light”
Line element see “Metric”
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) equivalence of the two theories spelled out 435
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity Chap 18 448—451 461—464 944—955
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity bar operation 436—438
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity curvilinear coordinates 441
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity effect of gravity on matter and photons 442—444
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity field equations 437—438 461f
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity formula for metric 438
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity gauge invariance of Riemann curvature 438
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity gauge transformations 438 441
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity global Lorenu transformations 4.V1
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity Lorentz gauge 438 441
| Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation as linearized limit of general relativity sketched 435
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) presentation from spin-2 viewpoint 179—186
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) self-inconsisiency of 180 443f
Linearized theory of gravity (same as Spin-2 theory in flat spacetime) self-inconsisiency of complete repair of leads to general relativity 186 424f
Lines of force diagram for gravitational waves 101
Lines of force never end, as core of Maxwell’s equations 420
Lines of force relation to honeycomb structure 102
Lorentz force law compared equation of geodesic deviation 35
Lorentz force law derived from Einstein’s field equations 473—475
Lorentz force law double role: defines fields and predicts motions 71—74
Lorentz force law energy change associated with 73
Lorentz force law for a continuous medium 570
Lorentz force law formulated, in flat spacetime 73
Lorentz force law in curved spacetime 201 568
Lorentz force law in language of energy-momentum conservation 155
Lorentz force law in language of forms 101—104
Lorentz force law in three languages 474
Lorentz frame, local closest to global Lorentz frame 207
Lorentz frame, local evidences for acceleration relative to 327
Lorentz frame, local mathematical representations of 217f 285ff 314f
Lorentz frame, local straight lines are geodesies of curved spacetime 312—324
Lorentz frame, local used to analyze redshift experiments 1056—1060 (see also “Inertial frame local”)
Lorentz gauge see “Gauge transformations and invariance”
Lorentz geometry, global 19—23
Lorentz geometry, global contrasted with Euclidean geometry 51
Lorentz geometry, global spacetime possesses, if and only if Riemann vanishes 284
Lorentz group 242
Lorentz invariance, experimental tests of 1054f
Lorentz transformations 66—69
Lorentz transformations boost 67 69
Lorentz transformations in spin-matrix language 1142—1145
Lorentz transformations in spin-matrix language velocity parameter 1145
Lorentz transformations infinitesimal antisymmetric matrix for 171
Lorentz transformations infinitesimal generator of 329
Lorentz transformations infinitesimal special case: boost along coordinate axis 80
Lorentz transformations key points 67f
Lorentz transformations matrix description of 66
Lorentz transformations post-Newtonian limit of 1086
Lorentz transformations rotation in a coordinate plane 67
Lorentz transformations used to annul Poynting flux 122 (see also “Rotations”)
Lorentz transformations velocity parameter in 67
Lorentz transformations way to remember index positions 66
Lowering indices see “Index manipulations”
Lunar orbit, experimental tests of general relativity using 1048 1116 1119 1127—1131
Machine with slots see under “Covariant derivative” “Metric” “Tensor”
Mach’s principle 490 543—545
Mach’s principle acceleration relative to distant stars 543
Mach’s principle and dragging of inertial frames 547 (see also “Dragging of inertial frames”)
Mach’s principle and Foucault pendulum 547
Mach’s principle and York’s formulation of initial-value problem 546
Mach’s principle dragging analoaous to magnetic effect 548
Mach’s principle dragging analoaous to magnetic effect inertial influence of distant stars 548
Mach’s principle dragging analoaous to magnetic effect sum-for-inertia in 549
Mach’s principle dragging analoaous to magnetic effect “flat” space as part of closed space in 549
Mach’s principle gives inertia here in terms of mass there 546
Magnetic flux, from integration of Faraday 99—101
Magnetic poles, absence of 80
Magnetostatics, plus covariance, gives magnetodynamics 80 106
Magnitude-redshift relation see under “Cosmology observational
Manifold, diflerentiable 10 13 241ff
Many-fingered time, and arbitrariness in slice through spacetime 713f 1184
Mass active vs. passive see “Cavendish gravitational constant”
Mass center of 161
Mass experimental, finite, as difference between two infinities 474—475
Mass hyperboloid 585
Mass inertial vs. gravitational 431 1051
Mass inertial, density of 159f
Mass-energy, density of see “Stress-energy tensor”
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) as geometric object residing in asymptotically flat spacetime 453 “active gravitational mass”) as geometric object residing in asymptotically flat spacetime 453
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) conservation law for 455 468—471 “active gravitational mass”) conservation law for 455 468—471
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) contribution of gravitational field to 467 “active gravitational mass”) contribution of gravitational field to 467
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) contribution of gravitational field to localizable to within a wavelength for gravitational waves 955f 964ff 969f “active gravitational mass”) contribution of gravitational field to localizable to within a wavelength for gravitational waves 955f 964ff 969f
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) contribution of gravitational field to not localizable in generic case 466ff “active gravitational mass”) contribution of gravitational field to not localizable in generic case 466ff
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) contribution of gravitational field to precisely localizable only for spherical systems 603f 803f “active gravitational mass”) contribution of gravitational field to precisely localizable only for spherical systems 603f 803f
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) denned by rate metric approaches flatness in extensor Chap. 19 “active gravitational mass”) denned by rate metric approaches flatness in extensor Chap. 19
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) denned by rate metric approaches flatness in general 453 455 “active gravitational mass”) denned by rate metric approaches flatness in general 453 455
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) denned by rate metric approaches flatness in linearized theory 448—450 “active gravitational mass”) denned by rate metric approaches flatness in linearized theory 448—450
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) measured via Kepler’s 1-2-3 law 450 457 636ff “active gravitational mass”) measured via Kepler’s 1-2-3 law 450 457 636ff
Mass-energy, total, of an isolated, gravitating system ( “active gravitational mass”) no meaning of for closed universe 457—459 “active gravitational mass”) no meaning of for closed universe 457—459
Matrix, inverse, explicit expression for 161 (see also “Jacobian” “Determinant”)
Matter in universe, luminous, mean density of 710f 761
Maxima, number of 318
Maximal analytic extension of a geometry 882
Maxwell energy density 140—141
Maxwell, dual 2-form representation of electromagnetic field, introduced 105 (see under “Electromagnetic field”)
Maxwell’s equations and conservation of energy-momentum 483
Maxwell’s equations component version in flat spacetime 80f
Maxwell’s equations deduced from “lines of force end only on charge” 79—81
Maxwell’s equations derived from physics on a spacelike slice 419—420
Maxwell’s equations derived from stress-energy and Einstein field equation 471—473
Maxwell’s equations for vector potential 569
Maxwell’s equations geometric version 88—89
Maxwell’s equations in curved spacetime 391 568
Maxwell’s equations in language of forms 112—114
Maxwell’s equations nowhere failing 1200 (see also “Electrodynamics” “Lorentz
Maxwell’s equations solution for particle in an arbitrary state of motion 121—122
Mean eccentric anomaly 648
Measurability of geometry and fields in classical theory 13
Measurement, possibilities defined by theory 1184
Measuring rods see “Rods”
Mercury, perihelion precession of see “Perihelion shift”
Meshing of local Lorentz frames 190—191
Metric coefficients in specific manifolds and frames see specific manifolds e.g. “Sphere or e.g. “Kerr
Metric compatibility with covariant derivative 313ff 353f
Metric components of in arbitrary basis 201 310f
Metric components of in Euclidean coordinates 22
Metric components of in Lorentz coordinates 22 53
Metric computation of connection coefficients from 210 216
Metric descriptions as line element 77 305 310
Metric descriptions as machine with slots 22 51—53 77 305 310f
Metric descriptions in component language 77 310f
Metric descriptions in terms of basis 1-forms 77 310
Metric descriptions introduced and defined 22
Metric descriptions summarized 77 305 310f
Metric determinant of components defined 202
Metric determinant of components, differentiated, gives contraction of connection coefficients 222
Metric determinant of components, variation of 503
Metric distilled from distances 306—309
Metric elasticity of space 426—428
Metric enters electromagnetism only in concept of duality 105 114
Metric role in Newton — Cartan spacetime 300 302
Metric role in spacetime of general relativity measured by light signals and free particles 324
Metric role in spacetime of general relativity measured by light signals and free particles, as “gravitational field” 399—400
Metric role in spacetime of general relativity measured by light signals and free particles, components not all predicted by geometrodynamic law 409
Metric role in spacetime of general relativity measured by light signals and free particles, test for local Lorentz character 311—312
Metric structure, and symplectic structure 126
Metric theories of gravity 1067ff
Metric theories of gravity experiments to test whether the correct theory is metric Chap. 38 1067
Metric theories of gravity PPN formalism as approximation to 1069
Microwave radiation see “Cosmic microwave radiation”
Minima, number of 318
Minkowski geometry see “Lorentz geometry”
Missing matter, “mystery of” 710 (see also under “Cosmology”)
Mixmaster oscillations damp chaos 769
Mixmaster universe 805—814
Mobius strip 96
Moment of inertia tensor defined 977
Moment of rotation as meaning of Einstein curvature 373—377
Moment of rotation conservation of 378ff 473
Momentum field, electromagnetic 497f 524
Momentum space 583ff 590
Momentum vector see “Energy-momentum 4-vector”
Momentum, in mechanics, as space rate of change of action 486—487
Moon effect on tides 44
Moon laser ranging to 1048 1130f
Moon orbit of tests of general relativity using 1048 1116 1119 1127—1131
Moon separation from Earth as gravitational-wave detector 1013f 1018
Moon shadow on Earth 24—26
Morse theory 318
Mossbauer effect 63 1056 1057
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



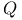 or
or 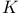
 “active gravitational mass”) as geometric object residing in asymptotically flat spacetime
“active gravitational mass”) as geometric object residing in asymptotically flat spacetime