Авторизация
Поиск по указателям
Bach E., Shallit J. — Algorithmic Number Theory (том 1)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Algorithmic Number Theory (том 1)Авторы: Bach E., Shallit J. Аннотация: "[Algorithmic Number Theory] is an enormous achievement and an extremely valuable reference." — Donald E. Knuth, Emeritus, Stanford University
Язык: Рубрика: Математика /Теория чисел /Вычислительная теория чисел /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1996Количество страниц: 516Добавлена в каталог: 21.05.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
50—52 278 58 59 63 66 151 12 46—47 49 51 12 47—49 147 7 16 47 3 45 46 51 56 65 50—52 61 64 278 51 52 278 2-regular sequence 338 3-conjunctive normal form 48 3-SAT 48 Abbott, W.L. 334 Abel's identity 25 26 38 Abel, N.H. 369 Abelian groups 30 116 138 Abelian groups, fundamental theorem of 138 152 Abramov, S.A. 98 Absolute Berlekamp algebra 164 189 190 Absolutely irreducible 136 Abundant number 93 94 Acceptance 45 Acyclic 57 Adams, W.W. 314 379 382 Addition chains 121 Additive number theory 259 Adleman — Manders — Miller algorithm 161 Adleman, L.M. 13 14 17 64 65 96 122 160 194 195 200 266 285 294 311 316 Admissible sequence 226 243 258 Agnew.G.B. 351 Agou, S. 197 Aho, A.V. xiii 150 152 326 345 Aieilo, W. 121 Aitken, A.C 347 Akbik, S. 350 Akl, S.G. 15 Akushskit, I.Ya. 312 Alagic, S. 99 Albert, A.A. 4 14 39 148 344 350 Alford, W.R. 251 276 313 315 316 algebraic 33 Algebraic integers 227 Algebraic number theory xiii 227—233 260—263 266 285 Algebraic number theory, computations 260 Algorithmic number theory xiv 1 2 9 Algorithms, Atlantic City 51 52 65 278 279 305 Algorithms, Las Vegas 51 52 65 168 278 279 293 Algorithms, Monte Carlo 51 52 65 278 279 Algorithms, polynomial-time 12 Algorithms, randomized 12 Alia,G. 121 ALICE 118 Allard, P.E. 355 Allouche. J.-P. xv xvi 150 338 339 Alphabet 44 AMM algorithm 160 183 Amo, S. 314 382 Amon, D. 196 Anderson, S.F. 66 Angluin, D. 353 Ankeny's theorem 178 245 253 Ankeny's theorem for number fields 231 262 263 Ankeny's theorem, explicit version 235 Ankeny, N.C 218 245 253 Ansari, A.R. 318 Anti-Chinese remainder theorem 107 122 Apostol, T.M. 38 246 323 335 367 368 Appel, K.I. 2 Approximate equality 26 29 Arbib, M.A. 99 Archibald, R.C. 14 312 Arithmometer 6 15 Arnault, F. 314 Artin symbol 230 262 Artin — Schreier polynomials 179 193 Artin — Scnreier equation 348 362 Artin — Whaples approximation theorem 118 342 Artin's conjecture 152 221 227 255—256 Artin's conjecture for inlinitely many bases 222 256 Artin's conjecture for number fields 263 Artin's conjecture for polynomials 135 Artin's conjecture, prime tuples and 256 Artin's constant 256 Artin's constant, complexity of 256 Artin, E. 118 148 149 152 153 205 221 255 262 342 345 348 353 362 Arwin, A. 196 Aryabhata 4 14 Aryabhatiya 4 98 Asano, Y. 351 Ash,D.W. 351 Associates 32 Associative law 30 Asymptotic differentiation 238 Asymptotic growth of functions, notation for 25 Asymptotic integration 27—28 39 Atkin, A.O.L. 13 314 353 Atlantic City algorithms 51 52 65 278 279 305 Augustine, St. 273 Automatic sequences 150 Averbuch, A. 152 Avizienis, A. 346 Ayoub, R.G. 15 Babai, L. 65 Babbage, H.P. 15 Baby-step giant-step algorithm 161 Bach, E. 99 153 195 198 200 201 253 255 256 264 325 326 328 332 344 352 353 356 359 369—371 373 379 386 Bachmann, P. 38 96 123 246 344 Backlund, R.J. 240 243 249 257 369 374 Bahbage, C. 6 Baillie, R. 253 305 314 382 Baker, C.L. 310 Baker, P.W. 120 Baker, R.C 225 257 Balasubramanian, R. 2 13 310 Bang, T. 318 Bannon, P.J. 14 Baratz, A.E. 315 Barlow. P. 14 96 Bartec, T.C. 148 Baruah, S.K. 342 Basis-factor algorithm 85 Bassalygo, L.A. 150 Bateman — Hom conjecture 259 Bateman, P.T. 14 259 375 Batui, C. 11 Baum, U. 152 Bays, C. 297 317 Bcntardi, D. 11 Beame, P.W. xv 65 Beard. J.T.B., Jr. 196 Beauchemin, P. 316 Beeger, N.G.W.H. 313 Beiler. A.H. 312 Bell, E.T. 7 15 Ben-Or algorithm 359 Ben-Or, M. 196 198 355 356 359 Benaissa, M. 148 Bengelloun, S.A. 317 Beniley, J.L. 96 Benin, P. 121 Benrand's postulate 225 238 Benrand's postulate for arithmetic progressions 367 Bergeron, R 121 Berlekamp algebra 164 190 Berlekamp algebra, absolute 164 189 190 Berlekamp algorithm 164 Berlekamp's algorithm 164 167 189 190 Berlekamp's algorithm, running time of 165 Berlekamp, E.R. 148 149 164 195—197 200 347 348 352 354 356 Berndt, B.C. 363 Bernoulli numbers 38 240 Bernstein, D. 99 326 Bernstein, L. 98 Berstel, J. 121 Bertrand, J. 225 238 367 Beth, T. 148 351 Bhargava, V.K. 148 351 Bicknell, M. 314 381 Bicycle-chain sieve 9 16 Biermann, O. 347 Biermann. K.-R. 309 310 Big-O notation 25 37 38 42 246 Big-omega notation 25 38 Big-theta notation 25 38 Bilharz, H. 152 Binary gcd algorithm 82—84 92 99 Binary gcd algorithm for polynomials 149 Binary gcd algorithm, extended 93 Binary gcd algorithm, variants of 93 Binary Jacobi algorithm 343 Binary method 102 121 Binary search 48 Binel form for Fibonacci numbers 330 Binet, J.P.M. 98 330 Binomial coefficients 35 Binomial equations in finite fields 155—163 189 195 Birch, B.J. 1 13 Birkhoff, G. 13 39 Bitlingsley. P. 248 Blake, I.E. 351 Blakley, G.R. 120 343 Blankinship, W.A. 96 Bleichcnbacher, D. 314 Block designs 196 Blokh, E.L. 196 Blum, M. xv 98 Blundon, W.J. 257—258 Bob 118 Boeffgen, R. 361 Bohman. J. 258 318 365 369 Bohr, H. 246 Bojanczyk, A.W. 98 Bokhari, S.H. 318 Bombieri, E. 251 Bond, D.J. 316 Boolean circuits 58 148 boolean formulas 48 Boos, P. 360 Boraing, A. 312 Borcl, E. 373 374 Borel — Cantelli lemma 373 374 Borho, W. 312 Borodin, A. 65 121 149 151 152 Borosh, I. 343 Borrell, D. 198 352 Borwein, P.B. 326 Bos, J. 121 Bose, N.K. 346 Bosma, W. 312 314 316 Bouniakowsky, V. 15 259 Bourbaki, N. 39 Boute, R.T. 38 Boyar, J. xv 148 372 Boyd, C. 315 Boys, C.V. 15 Bradley, G.R 96 Brahmagupta 4 14 Brancker, T. 1 Brassard, G. 64 316 Brauer, A. 121 318 Brenljes, A.J. 98 Brent, R.P. 39 98 99 149 249 257—259 310 317 Bressoud, D.M. xiv Breusch, R. 320 Brewer, B.W. 312 Brezinski, C. 98 Brickell, E.F. 120 121 Briggs, W.E. 369 Brillhart, J. xv xvi 8 10 14 15 310 311 380 385 Brlek, S. 121 Brodnik, A. xv Brooks, A.S. 245 Browder, F.E. 16 Brown, J. 309 Brown, Jr.J.L. 98 Bruckman, P.S. 314 Brun — Titchmarsh theorem 263 Brun. V. 97 206 258 263 317 Bshouty, N. 152 Buchmann, J.A. 99 200 260 Buck, R.C. 318 Buell, D.A 10 16 312 Buhl, J. 312 Buhler, J.P. 2 13 312 Bum's constant 258 Bum's constant, intractability of 258 Bumby, R.T. 353 Burgess, D.A. 123 201 253 255 373 Burthc, Jr., R.J. 253 317 Burtsev. V.M. 312 Butler, M.C.R. 196 198 Cadwell, H. 256 257 Cahen, E. 368 Calculators, mechanical 6 8 15 249 Caldwell, C.K. 312 Callan, D. 319 Calmel, J. 148 198 Calude. C. 315 Cames, R. xv Camion, P.R. 149 196 Campbell, D. 311 Campbell-Kelly, M. 16 Canonical representative 101 Canonical representative for gcd of polynomials 130 Canonical representative for multiplicative inverse 102 Cantelli, F.P. 373 374 Cantor — Zassenhaus algorithm 167—168 190 Cantor, D.G. 11 148 151 167 196 197 353 355 Capoeelli, R.M. 122 Cappello, P.R. 122 Cardano, formula of 184—185 200 363 Cardano, G. 200 Carissan, E. 8 15 Carissan, P. 8 Carlitz, L. 152 356 358 360 364 Carmichael lambda function 275 Carmichael lambda function for polynomials 194 Carmichael numbers 227 266 275—279 313 314 Carmichael numbers, infinitely many 276 Carmichael, R.D. 310 312 313 Caron, T.R. 16 Cartier, P. 123 Carvaho, J. 312 Casde, C.M.A. 97 Cassels, J.W.S. 262 Casteran, P. 121 Cataldi, P. 1 308 310 Cauchy principal value 246 Cauchy's theorem 138 Cauchy, A.L. 149 199 200 313 360 363 Caviness, B.E. 98 CayIey, A. 149 CEILING 19 Central limit theorem 256 Cerbone, G. 122 Cerlienco, L. 346 Certificate 279 Cesaro, E. 36 238 324 332 335 367 CFA algorithm 76
Реклама
 |
|
О проекте
|
|
О проекте



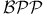
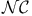
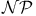

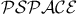 -complete
-complete