Авторизация
Поиск по указателям
Bach E., Shallit J. — Algorithmic Number Theory (том 1)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Algorithmic Number Theory (том 1)Авторы: Bach E., Shallit J. Аннотация: "[Algorithmic Number Theory] is an enormous achievement and an extremely valuable reference." — Donald E. Knuth, Emeritus, Stanford University
Язык: Рубрика: Математика /Теория чисел /Вычислительная теория чисел /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1996Количество страниц: 516Добавлена в каталог: 21.05.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Dubner, R. 10 16 Dubner.H. 10 16 312 313 Duboc, C. 121 Dubois, R. 313 Ducray, S. 247 Dudley, U. 318 Duncan, R.L. 98 Dunten, B. 317 Duparc, H.J.A. 313 Dupre, A. 80 98 Dussaud. R. 313 Dynamic programming 329 Earle, J.G. 66 Eastman, W.L. 152 Eberly.W. 152 Ecker, M.W. 340 Edgar, G.A. 319 Edges 57 Edmonds, J. 12 16 64 Edwards, H.M. 38 245 246 249 251 369 Egecioglu, O. 121 Ehrman, J.R. 311 375 Eisenstein, G. 119 123 343 350 Elder, J.D. 9 Eldridge, S.E. 120 121 Elia, M. 195 Elkies, N.D. 13 Elliott, P.D.T.A. 248 249 253 255 Elliptic curve pseudoprimes 314 Elliptic curves 266 Elliptic curves, polynomial factorization and 201 Elliptic curves, square roots mod p and 195 Empty product 20 Endoes — Kac theorem 248 ENIAC 9 entropy 65 Epasinghe, P.W. 98 Eppstein, D. 64 Er, M.C. 122 ERATOSTFINES algorithm 296 Eratosthenes 236 265 Eratosthenes, sieve of 4 5 204 Erdoes, P. 121 206 246 248 249 253 257 304 313 314 335 376 ERH see extended Riemann hypothesis Ernvall, R. 2 13 Error, one-sided 50 278 Error, two-sided 51 Escott, EB. 122 314 382 Estes, D.R. 123 Euclid 1 4 20 96 204 205 273 303 Euclidean algorithm 41 67—70 Euclidean algorithm for polynomials 127—130 143 Euclidean algorithm for polynomials, running time 149 Euclidean algorithm for polynomials, uniqueness 347 Euclidean algorithm for resultants 347 Euclidean algorithm in real quadratic fields 98 Euclidean algorithm, bit complexity of 68 70 Euclidean algorithm, extended 4 70—73 93 Euclidean algorithm, least-remainder variation 79—82 98 Euclidean algorithm, musical theory and 97 Euclidean algorithm, number of division steps 41 Euclidean algorithm, subtractive version 97 Euclidean algorithm, worst-case analysis 69 Euclidean Domain 98 EUCLUD algorithm 67 Euler liars 279 Euler phi function 21 Euler phi function for polynomials 194 Euler phi function, estimates 237 Euler phi function, explicit bounds for 234 Euler phi function, formula for 35 Euler pseudoprimes 277 305 313 Euler witness 280 Euler — Maclaurin expansion 39 Euler — Maclaurin expansion for gamma function 240 Euler — Maclaurin expansion for zeta function 240 250 Euler's constant 26 39 Euler's criterion 110 122 143 178 186 242 277 Euler's summation formula 26 36 207 Euler's theorem 35 101 Euler, L. 2 4 5 14 15 21 26 38 39 98 111 121 122 205 242 245 250 265 273 303 309 347 375 Evans, R.J. 363 Evdokimov, S.A. 199—201 EVEH NUMBERS 45 60 Even pseudoprimes 313 Even, S. 121 Ewing. J. 309 Expected polynomial time 51 Explicit formulas 213 250 Exponent of a group 31 275 Exponent of a permutation group 238 Exponent of a polynomial 135 Exponential integral 365 EXTENDED EUCLID algorithm 72 Extended Euclidean algorithm 4 70—73 93 Extended Riemann hypothesis 123 159 178 182 185 187 205 216 239 251 252 314 Extended Riemann hypothesis, applied to algorithms 252 Extended Riemann hypothesis, empirical evidence for 252 Extended Riemann hypothesis, heuristic argument for 241 Extended Riemann hypothesis, true on average 251 Extended Riemann hypothesis, weak 253 Extended Riemann hypothesis, П 241 Extension 33 Extension, finite 33 Extension, separable 143 Factor 48 307 Factor refinement see gcd-free basis Factor stencils 9 15 Factor tables 13 Factor tables for polynomials 196 Factorization into products of primes 20 Factorization mod 174—175 Factorization of matrices 195 Factorization of polynomials over finite fields 155 163—168 195—198 200—201 Factorization of polynomials over finite fields, distinct degree 171 Factorization of polynomials over finite fields, special cases 200 201 Factorization over p-adic numbers 176 199 Factorization, integer 1 3 7 9 42 47 148 Factorization, integer, continued-fraction algorithm 10 Factorization, integer, Morrison — Brillhart algorithm 10 Factorization, integer, quadratic sieve algorithm 10 Factorization, integer, trial division 265 Factorization, integer, uniquc 20 35 38 Factorization, polynomial 3 Factorization, polynomials over finite fields 125 189—190 Factorization, polynomials over finite fields, distinct degree 198 Faddeev, D.K. 196 Fagin, B.S. 64 False witness 314 Fast Fourier Transform 150 151 369 Fateman, R.J. 121 Feit, W. 198 Felkel, A. 6 Feller, W. xiii 247 373 374 FELLOWS — KOBLITZ algorithm 268 Fellows, M.R. 311 Fendel, D. 15 Feng. G.-L. 148 Fenn, S.T.J. 148 Ferguson, H.R.P. 98 Fermat liars 275 305 Fermat numbers 10 267 272 273 Fermat numbers, factorization of 119 Fermat primes 243 Fermat's theorem 21 35 38 101 265 Fermat's theorem, primality proofs and 266—272 Fermat, P. 2 4 14 38 Ferrier, A. 10 16 309 Feynman, R.P. 243 376 FFT see fast Fourier transform fibonacci 265 Fibonacci numbers 37 68 95 122 Fibonacci numbers, Binet form for 330 Fibonacci numbers, computing large 60 103 104 Fich, F.E. 151 Ficken, F.A. 96 Fiduccia, C.M. 122 338 Field of algebraic numbers see number fields Field, definition of 33 Field, extension 33 Field, extension, normal 230 Field, finite see finite fields Fiirer,M. 315 Finck, P.J.E. 96 97 Findlay, P.A. 122 Finite abelian groups, fundamental theorem of 31 Finite automata 150 362 Finite characteristic 34 Finite extension 33 Finite fields 125—153 155—201 344—352 Finite fields, construction of 155 171—173 178—182 193 198—199 Finite fields, existence of 125 Finite fields, hardware for 132 351 Finite fields, inversion 143 Finite fields, isomorphism between 172—173 192 199 Finite fields, models of 126 145—148 Finite fields, normal bases for 191 Finite fields, parallel algorithms for 151 Finite fields, software for 148 Finite fields, uniqueness of 126 Finite groups 30 Finite groups, cyclic 147 Finitely generated 30 Finn, J. 65 315 Fischer, P.C. 318 Fitch, J. 325 Flad, J.-P. 15 Fleischmann, P. 356 Fletcher, C.R. 38 Flipponi, P. 314 FLOOR 19 Floyd, R.W. 95 335 Fogels, E.K. 263 Forcade, R.W. 98 Ford, K. 335 Format's last theorem 2 13 Format's last theorem, heuristic arguments 243 376 Formula 299 Formula, good 300 Four-color conjecture 2 Fraleigh, J.B. 39 Frame, J.S. 98 123 Frandsen, G.S. xv 148 198 350 356 Fredman, M.L. 152 385 Fridlender, V.R. 372 Friedl, K. 372 Friedlander, J.B. 261 373 Friedmann, A. 195 Frobenius automorphism 133 Frobenius map 133 134 136 143 159 164—166 180 196 Frobenius map, absolute 136 189 Frobenius, F.G. 15 152 Froeberg, C.E. 14 369 Froehlich, A. 148 262 Fruechtl, K. 258 Function, multiplicative 23 Function, polynomial-time computable 49 Fundamental Theorem of Arithmetic 20 35 38 Fundamental theorem of finite abelian groups 31 Fung, G.W. 15 Furry, W.R. 365 Gaal, L. 152 Gage, P. 309 Gallagher, P.X. 251 Galois group 34 133 Galois group, relative 133 Galois theory xiii 133 227 Galois, E. 15 148 197 198 Gandhi, J.M. 306 318 382 Gao, S. 351 356 Gardiner, V. 249 Gardner, M. 15 96 332 Garey, M.R. xiii 64 Gate 58 Gauss sums 285 286 316 Gauss's lemma 117 Gauss, C.R. 1 5 15 38 106 111 122 152 194 197 199 200 204 205 236 245 253 265 310 344 363 Gaussian integers 38 98 Gaussian periods 147 179 181 193 200 378 GCD see greatest common divisor gcd-free basis 84 326 GCD-FREE Basis algorithm 89 gcd-free basis for polynomials 143 344 Ge, G. 99 Gegenbauer. L. 198 247 383 Geiselmann, W. 351 Gel'fond, A.O. 246 Genaille, H. 7 15 Generalized Riemann hypothesis 64 168 178 182 184 193 194 205 229 252 255 285 292 Generalized Riemann hypothesis, empirical evidence for 261 Generating set, bounds for, assuming ERH 220 Generating set, bounds for, averaged 255 Generating set, bounds for, heuristics 242 253 Generator 116 Gennero, M.C. 197 Gentleman, W.M. 121 Gerardin, A. 7—8 15 Gerlach, H.W. 316 380 Gibson, J.K. 120 Giesbrecht, M 197 350 356 369 370 Gilbert, W. xv Gill, J. 65 327 Gillies, D.B. 16 309 311 375 Gioia, A.A. 121 Glaisher, J.W.L. 13 15 257 258 Godel's thesis 11 Goedel, K. 11 12 16 310 Goel, A. xv Goettfert, R. 356 Gohl, G. 365 Goldbach's conjecture 1 259 Goldbach, C. 259 Goldreich. O. 96 Goldschmidt, R.E. 66 Goldstein, C. 38 Goldstein, L.J. 260 261 263 Goldstine, H.H. 14 Goldston, D.A. 257 Gollmann. D. 351 Golobew, W.A. 259 Golomb, S.W. 95 149 197 257 317 318 335 382 Golovanov, P.N. 151 Good, L.J. 248 311 375 Goodman, A.W. 99 Goodslein, R.L. 318 Gordon, D.M. 121 314 Gordon, J.A. 317 334 352 Goutier, C. 316 Graduate course outline xiii Graham, R.L. 38 39 339 Graham, S.W. 313 Gram, J.P. 249 250 256 365 Granville, A. 13 251 256 257 276 313 315 316 Greatest common divisor 3 34 67—99 186 Greatest common divisor for polynomials 128 360 Greatest common divisor on rational numbers 34 Greatest common divisor, analogue method for 96 Greatest common divisor, billiards and 92 Greatest common divisor, binary algorithm for 82—84 92 99 Greatest common divisor, binary algorithm for, variants of 93
Реклама
 |
|
О проекте
|
|
О проекте



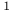 formula for
formula for 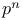
![$(\mathbb{Z}[i])$](/math_tex/2c0c436afe5ca9ff323688855d805fd882.gif)