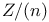Авторизация
Поиск по указателям
Bach E., Shallit J. — Algorithmic Number Theory (том 1)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Algorithmic Number Theory (том 1)Авторы: Bach E., Shallit J. Аннотация: "[Algorithmic Number Theory] is an enormous achievement and an extremely valuable reference." — Donald E. Knuth, Emeritus, Stanford University
Язык: Рубрика: Математика /Теория чисел /Вычислительная теория чисел /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1996Количество страниц: 516Добавлена в каталог: 21.05.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Landau, E. 37—39 205 228 238 246 247 251 255 260 261 324 346 366—368 Lander, L.J. 2 13 243 257 375 Landrock. P. 317 Landry, F. 311 Landsberg, G. 352 Lang, S. 39 148 199 260 261 344 349 352 360 377 Langemyr, L. 152 Language 44 Language classes 44—46 Language, accepted by algorithm 45 Lapidus, M.L. 249 Laplace transforms 213 Laplace, P.S. 374 Larsen, G.N. 148 Larson, R.G. 314 Las Vegas algorithms 51 52 65 157 168 278 279 293 Law of Large Numbers 212 247 Lawrence, F.W. 8 15 Laws, Jr.B.A. 148 Lazars, D. 99 196 347 Lazarus, R, 249 Le-Ngoc, T. 348 354 Least common multiple 34 Least common multiple for several inputs 34 Least common multiple of binomial coefficients 35 Least common multiple on rational numbers 34 Least common multiple, computation of 20 Least common multiple, definition of 19 Least common multiple, formula for 34 Least common multiple, relationship to gcd 34 Least integer function 19 Lebesgue, V.-A. 119 123 319 343 Lebmer, D.H. 2 8—11 13—16 97 171 194 197 249 255 265 267 279 300 309—314 317 318 358 363 365 380 Lebon, E. 13 Legendre symbol 101 110—111 123 141 Legendre symbol, efficient computation of 111 Legendre symbol, pseudo-random behavior of 254 Legendre, A.M. 15 111 121—123 195 199 204 205 215 245 251 257 306 320 353 365 Leger, E. 96 Lehman, R.S. 2 13 249 Lehmanti, D.J. 305 315 382 386 Lehmer, D.N. 1 9 13 15 16 310 365 Lehmer, E. 2 13 14 255 314 352 363 Leibniz, G.W. 6 38 Leighton, F.T. 311 329 Leiserson, C.E. xiii 328 Lejeune-Dirichlet, P.G. see Dirichlet P.G.L. Lemer, M 16 Lemoine, E. 326 Lempel, A. 350 Lenstra, A.K. xv 10 197 201 285 316 Lenstra, Jr.H.W. xv 1 13 99 121 148 194 199—201 256 260 285 310 311 316 326 344 350 351 356 373 375 379 380 385 386 Leonard, P.A. 152 Leong, B. 121 Leung, J.Y.-T. 342 Levin, G. 122 Levin, L. 64 Levy, P. 258 Lewis, D.J. 199 Li, X.M. 196 Liang, J.Y.Y 369 Liars 314 Liars, Euler 279 Liars, Fermai 275 305 Liars, strong 281 282 Lidl, R. 148 194 199 314 362 Lieberherr, K. 315 Lieuwens, E. 314 Lifchitz, H. 310 Lilley, S. 15 Lin-Kriz, Y. 96 Lind, D. 314 381 Lindemann, F.A. 319 see Lord Lindgren, H. 318 Lindhurst, S. 194 Linear algebra, complexity of 195 376 Linear congruemial generator 115 Linear recurrence 115 122 131 Linnik's theorem 223 241 242 245 256 Linnik's theorem for number fields 231 263 Linnik's theorem for number fields, explicit version 235 Linnik's theorem, assuming ERH 223 Linnik's theorem, assuming ERH, explicit version 235 Linnik, Yu.V. 223 241 242 245 256 Lipton, R.J. 121 122 Litow, B.E. 148 149 151 Littlewood, J.E. 38 247 248 252 258 259 366 Liule-o notation 25 38 Liverance, E. 379 Livingston, M.L. 263 Lloyd, D.B. 196 Lloyd, S.P. 359 LMO algorithm 302 Loeh, G. 313 Log-space uniform 58 Logarithmic integral 209 246 365 367 Looff, W. 308 309 Loop unrolling 96 Loos, R.G.K. 123 198 Lovasz, L. 201 Low, M.E. 252 Lubiw, A. 329 Lucas numbers 305 Lucas pseudoprimes 314 Lucas sequences 195 Lucas — Lehmer test 273—275 Lucas, E. 6 7 9 10 15 265 267 309—312 Lueh, G. 259 Lugiez, D. 361 Luk, F.T. 99 149 Lund, C. 372 Luneburg, H. 356 Luo, X. 318 Lutz, D. 64 Ma, K. 149 Mac Lane, S. 39 Machines, Cray XMP 10 Machines, ENIAC 9 Machines, EPOC 10 Machines, IBM 360 11 Machines, microcomputers 16 Machines, Sun 10 Machines, supercomputers 16 Machines, SWAC 10 MacLagan-Wedderbum, J.H. 148 Maclaurin, C. 39 Macsyma 11 Maeder, R.E. 63 122 Mahnke, D. 379 Maier, R 249 256 257 Mairson, H.G. 317 Majewskt, B.S. 96 Makowski, A 314 Mallette, R. 121 Malm, D.E.G. 305 315 381 Malo, E. 305 314 381 382 Malula, D.W. 99 Manasse, M. 10 Mandelbaum, D.M. 99 Manders, K.L. 14 64 160 194 195 Mann, H.B. 196 379 Mansour, Y. 65 96 Many-one reductions 47 49 64 353 Mapes, D.C. 318 Maple 11 Marci, A.E. 310 Marcus, D.A. 98 260 Marsaglia, G. 3 14 Marsh, D.C.B. 319 Martinelli, E. 121 Mason, T.E. 8 15 Massey, J.L. 149 351 Massias, J.P. 368 Mathcws,G.B. 200 318 Mathematica 1 Matiyasevich, Yu.V. 12 14 17 250 371 Matrices, circulant 144 Matrices, computing powers of 144 Matrices, enumeration by rank 352 Matrices, multiplication of 55 Matrices, multiplication, complexity 352 Matrices, nonsingular 147 Matsumoto, T. 121 Matthews, K.R. 96 Matthews, R.W. 148 314 Maurer, U.M 314 317 Maximal ideals 32 Mays, M.E. 98 McCarthy, D.P. 121 McCoy, N. 352 McCurdy, K.J. 10 16 McCurley, K.S. xv 121 242 256 263 264 373 McDaniel, W.L. 314 McDonald, B.R. 152 352 360 McEIiece, R.J. 352 355 Mclnnes, J. 369 370 McMillan, E.M. 39 Mead, C.A. 65 Meertens, L. 38 Meidanis, J. 122 123 Meijer, A.R. 97 Meissel, E.D.F 300 318 Meller, N.A. 249 Menezes, A.J. xv 196 197 201 Mersenne numbers 5 6 9 267 272—274 Mersenne numbers, factorization of 119 Mersenne numbers, Lucas' test for primality of 7 15 Mersenne numbers, strong prime tuples conjecture and 376 Mersenne primes 10 243 274 303 Mersenne primes, density of 375 Mersenne primes, largest 10 Mersenne, M. 4 5 14 Mertens's conjecture 248 Mertens's theorem 205 210 237 247 Mertens's theorem as sieve 247 Mertens's theorem for arithmetic progressions 251 Mertens's theorem, assuming Riemann hypothesis explicit bounds 249 Mertens's theorem, explicit version 234 Mertens, E 2 205 209 237 245 332 Mertens, S. 312 Metropolis, N. 249 Metsankyla, T. 2 13 Meyer, A.R. 64 65 122 Meyer, R 351 Michel, P. 65 Microcomputers 16 Mignotte, M. 63 194 196 198 201 315 Mihailescu, P. 311 Miller — Rabin algorithm 282 Miller — Rabin test 281—283 294 304 314 Miller — Rabin test, compared to Solovay — Strassen 283 Miller, G.L 12 96 99 115 160 194 195 284 314 315 386 Miller, J.C.P. 122 255 309 338 Miller, V.S. 300 318 356 365 385 Miller, W. 368 Milller, J. 308 Mills, W.H. 306 318 382 Minimal polynomials 34 134 144 146 152 352 Minimal polynomials for primitive elements 352 Minkowski, H. 261 Minsky, M.L. 310 327—329 Mirimanoff, D. 356 Misra, J. 317 318 Mitchell, H.H. 260 Mitrinovic, D.S. 263 Mitsui, Т. 261 Miyamoto, I. 314 Mo, Z. 314 MOD 21 Modular arithmetic 21 Modulus 115 Moebius function 2 23 38 134 Moebius function for polynomials 191 Moebius function in finite fields 132 143 Moebius function, parallel complexity of 121 151 Moebius inversion 23 35 135 Moebius, A.E 38 191 Moenck, R.T. 97 150 201 347 Monagan, M.B. 13 Monet, S. 64 Monic 33 Monier, L. 305 314 Monoids 30 Monte Carlo algorithms 51 52 65 278 279 Montgomery, H.L 250 253 263 379 Montgomery, P.L. xv 120 151 Montolivo, E. 352 Moore, E.H. 148 Moore, E.R. 64 Moore, T.E. 99 Morain, E. 15 121 313 Moral certainty 310 Moran, A. 259 Moree, P. 367 Morehead, J.C. 312 Morii, M. 148 Morita, H. 120 Moroz, B.Z. 253 Morrison, D.R. 148 Morrison, J.F. 199 Morrison, M.A. 10 11 311 Moser, L. 317 318 325 Most-wanted number 9 Motwani, R. 65 Mueller, W.B. 314 Muir, Т. 98 Mullin, R.C. 351 Multiplication, fast algorithms for 60 63 Multiplicative function 23 Multiplicative inverse in 102 Multiplier 115 Munro, L. 152 Murala, L. 255 256 Musser, D.R. 249 Muurer, W.D. 123 Nagasaka, K. 344 Nair, M. 246 Naive bit complenity 7 10 42—44 59 Naive space complexity 55 Narkiewicz, W. 252 255 260 National Security Agency 4 Nazarevsky 312 Nebgen, E. 312 Needham, J. 122 313 Nelson, H.L. 309 Nemeth, E. xv Netto, E. 149 Neudccker, W. 249 Neukirch, J. 262 Neumann, B.H. 382 Nevin, N. 64 Newman, D.J. 247 Newton, I. 348 Newton, method of 176 Nickel, L 16 309 Nicolas, J.-L. 14 263 310 316 368 Nicomachus 14 Niebuhr, W 313 Niederreiter factorization algorithm 190 Niederreiter, H.N. 148 194 199 356 362
Реклама
 |
|
О проекте
|
|
О проекте