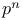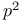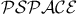Авторизация
Поиск по указателям
Bach E., Shallit J. — Algorithmic Number Theory (том 1)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Algorithmic Number Theory (том 1)Авторы: Bach E., Shallit J. Аннотация: "[Algorithmic Number Theory] is an enormous achievement and an extremely valuable reference." — Donald E. Knuth, Emeritus, Stanford University
Язык: Рубрика: Математика /Теория чисел /Вычислительная теория чисел /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1996Количество страниц: 516Добавлена в каталог: 21.05.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Nielsen, N. 365 Nievengloski, G.H. 98 Nim-multiplication 349 Niven, I. 318 325 Noll, c. 16 309 Nondctenninistic polynomial time 46 Nondeterministic algorithm 46 Nondeterministic random access machine 60 Nonresidues 178 183 186 241 252 253 Nonresidues in finite fields 200 Nonresidues, bounds for 242 253 372 Nonresidues, bounds for, averaged 253—254 Nonresidues, pseudo-random behavior of 217 253 Nonresidues, quadratic see quadratic nonresidues Norm 134 136 152 157 Norm in a number field 227 Norm in a number field, computation 243 Norm of an ideal 228 Norm, complexity of 347 Norm, computation of 144 Normal bases 145 148 151 Normal bases of primitive elements 356 Normal bases, constructing 356 Normal bases, density of 350 Normal bases, polynomial factorization and 356 Normal bases, special 350 Normal subgroups 31 NORMAL-POWER algorithm 350 Norman, A.C. 314 Norre, C. 312 Norris, M.J. 120 Norton, G.H. 97 99 149 334 Norton, K.K. 253 Number fields 227 Number fields, degree 227 Number fields, discriminant 227—228 244 Number fields, integral basis 227 244 Number fields, norm 227 228 Number fields, norm, computation 243 Number fields, normal extension of 230 Number fields, presentation of 227 Number fields, trace 227 Number fields, trace, computation 243 Number fields, zeta function see zeta function Dedekind NUMBER OF DIVESORS TABLE algorithm 298 Number of prime divisors, estimates 237 Number of prime divisors, explicit bounds for 234 Number of prime divisors, normal distribution 248 Number theory, computational complexity and 3—4 Number theory, probabilistic 248 Number-of-divisors function, average order of 26 Number-of-divisors function, estimates 237 263 Number-of-divisors function, explicit bounds for 234 Number-of-divisors function, formula for 35 Odlyzko, A.M. xv 2 13 64 250 261 263 291 300 318 365 385 Odoni, R.W. 255 Oesierte, I. 264 Ofman, Y. 63 65 151 326 345 Ogiwara, M. 317 Oldham, I.B. 196 Olivier, M. 11 369 Olivos, J. 121 Omura, J.K. 351 One-sided error 50 278 Onyszchuk, I.M. 351 Oracle 49 Order of a group element 31 Order, multiplicative 9 101 147 Order, multiplicative, efficient computation of 115 Ordinary leaves 302 Ore, O. 152 153 260 318 Orton, G.A. 14 Orup, H. 122 Oswald, A. 314 Out-degree 58 OwingsJ.C 314 p-adic numbers 175—176 192 199—262 p-th roots in characteristic p 162 p-th roots, mod 192 p.i.d. (principal idea) domain) 33 Pajunen, S. 386 Pall, G. 123 Pan, V. 96 Papadimitriou, M 318 Papert, S. 310 Parady, B.K. 258 312 Parallel computation 9 16 57—59 Parberry, E.A. 314 Parberry, I. 318 PARI 11 Parikh, S.N. 99 Parkin, T.R. 2 13 243 257 375 Partial quotients 75 Partition 49 329 Partition problem 48 Pascal, B. 6 Patashnik, O. 38 39 Paterson, M. 38 Pathology 192 Patterson, C.D. 16 Paxson, G.A. 312 Peano arithmetic 372 Pei, D. 351 Pellet, A.-E. 152 356 362 Penk, M.A. 258 312 334 Penttonen, M. 65 Pepin's test 272 312 Pepin,T. 311 312 Peppard, L.E. 14 351 Peralta, R.C. 253 353 Perfect numbers 5 273 Perfect numbers, even 273 303 Perfect numbers, odd 273 Perfect powers, complexity of determining 59 242 Permutation group, cycles in 359 Permutation group, exponent of 238 Permutations, random polynomials and 359 Perrin, R. 305 382 Pervushin, J.M. 7 15 367 Peterson, I. 16 309 Peterson, W.W. 148 Petr, K. 196 198 Pettorossi, A. 122 Phi function 21 Phi function for polynomials 194 Philippe, J.-L. 318 Phong, B.M. 314 Piarron de Mondesir, E.S. 318 Picutti, E. 308 309 Pieper, H. 123 Pierce expansion 94 95 Pila, J. 200 326 Piltz, A. 251 256 258 Pin, J.-E. 310 Pinch, R.G.E. 199 313—315 Pincin, A. 351 Pintz, J. 311 317 380 Piontas, M. 148 Pippenger, N. 66 121 Piras, F. 346 Pitteway, M.L.V. 97 Plaisted, D.A. 64 317 Planck, M. 241 Plankensteiner, B. 97 Pocklington, H.C. 7 8 15 121 310 353 Pohst,M. xiv 260 Poilin, J.M. 314 381 Poisson distribution 256 Poisson process 256 Poletti, L. 259 Poli, A. 197 Polkinghorn, Jr.J.E. 196 Pollard, J.M. 311 Polvani, G. 256 Polya — Vinogradov inequality 263 Polynomial rings 32 125 Polynomial time 12 45 54 Polynomial time, expected 51 Polynomial-cost RAM 52 Polynomial-time computable function 49 Polynomial-time Turing reductions 50 Polynomials over finite local rings 360 Polynomials, Artin — Schreier 179 193 Polynomials, cyclotomic 147 Polynomials, irreducibility tests for 168 172 198 Polynomials, irreducible 34 Polynomials, mod 192 Polynomials, multiplication of 143 Polynomials, prime-producing 6 Polynomials, primitive, number of 152 Polynomials, sparse representation of 163 Pomerance, C. 10 16 195 251 257 263 276 285 291 295 310 311 313—316 380 381 Popadic, M.S. 263 Porter, J.W. 97 Post, E.L. 12 16 64 Potler, A. 257 Poulet, P. 314 POWER algorithm 102 Power algorithm, iterative implementation 103 114 Power algorithm, recursive implementation 102 Power residues, recognition 351 Powers, D.M. 66 Powers, R.E. 10 Prabhu, K.A. 346 Prachar, K. 246 253 258 368 369 Prasad, T.V.S.R.V. 310 Pratt tree 269 Pratt, V.R. 311 Preste, M.D. 196 Primality testing 45 266 Primality testing of polynomials 168 172 198 Primality testing, Pepin's test 312 Primality testing, randomized algorithms for 12 278—283 Prime factorization 20 Prime fields 125 Prime ideal theorem 228 261 Prime ideal theorem for arithmetic progressions 263 Prime ideal theorem, equivalent forms 261 Prime ideal theorem, holds up to constant factor 261 Prime ideals 33 228 Prime ideals, degree of 228 Prime ideals, density 243 Prime ideals, density of 228 261 Prime ideals, ramified 262 Prime ideals, splitting of 229 230 262 Prime number sieves 295—299 Prime number theorem 20 29 204 236 245—247 Prime number theorem for arithmetic progressions 215 245 251 Prime number theorem for arithmetic progressions, assuming ERH 217 Prime number theorem for arithmetic progressions, equivalent forms 251 Prime number theorem for arithmetic progressions, explicit version 235 263 Prime number theorem for cosets of 215 Prime number theorem for cosets of 217 Prime number theorem, analytic proof 210—211 239 Prime number theorem, assuming Riemann hypothesis 212 Prime number theorem, assuming Riemann hypothesis, explicit bounds 249 Prime number theorem, elementary proof 206 246 Prime number theorem, explicit versions 233 Prime number theorem, heuristic argument for 236 Prime number theorem, holds up to constant factor 207—208 246 Prime number theorem, intuitive argument for 206—207 238 246 Prime number theorem, probabilistic interpretation 209 Prime number theorem, sharpest known version 209 Prime numbers 20 Prime numbers in an arithmetic progression 348 Prime numbers in arithmetic progressions 245 251 Prime numbers in arithmetic progressions, bounds for 222—223 241 256 Prime numbers in arithmetic progressions, density 235 Prime numbers in arithmetic progressions, finding 224 241 Prime numbers in arithmetic progressions, heuristic arguments 242 Prime numbers in arithmetic progressions, infinitely many 215 Prime numbers in cosets of 224 Prime numbers of polynomial form 259 Prime numbers, approximately 247 258 Prime numbers, approximations for 238 Prime numbers, arithmetic progression of 259 Prime numbers, arithmetic progression of, longest known 259 Prime numbers, counts of 247 256 Prime numbers, estimating sums over 28 Prime numbers, gaps between 224—225 242 243 256 257 Prime numbers, infinitely many 20 204—205 236 365 Prime numbers, random 265 Prime numbers, statistical mechanics and 249 Prime numbers, tables or 6 13 Prime numbers, tuples of 226—227 Prime numbers, twin nee twin primes Prime-producing polynomials 6 Prime-reciprocal constant 233 237 264 PRIMES 45 46 Primes, explicit estimates for functions of 233—236 PRIMETEST algorithm 294 Primitive polynomials 135 352 Primitive polynomials, number of 144 152 Primitive roots 109 116 252 Primitive roots, bounds for 255 Primitive roots, bounds for, assuming ERH 221 241 Primitive roots, bounds for, averaged 255 Primitive roots, bounds for, heuristics 242 Primitive roots, bounds for, mod 255 Primitive roots, search procedures 255 Principal ideal 33 Principal ideal domain 33 143 Pritehard, P. 259 317—318 Probabilistic number theory 248 Probabilistic primality tests 278—283 Prodinger, H. 339 Prom's test 273 Proof, polynomial-length 46 Protasi, M. 122 Proth, K. 267 312 Pseudo-code xiv Pseudo-polynomial time 329 Pseudo-random number generation 3 115 Pseudoprimes 275—277 305 313 314 Pseudoprimes, 56 Pseudoprimes, composite 313 Pseudoprimes, elliptic curve 314 Pseudoprimes, Euler 277 305 313 Pseudoprimes, even 313 Pseudoprimes, Fermat 275 Pseudoprimes, Lucas 314 Pseudoprimes, ordinary 275 Pseudoprimes, strong 277 281 313 Public-key cryptography 12 Purdy, C.N. 98 Purdy, G.B. 93 98 99 252 334 Putnam, H. 12 Pythagoreans 204 245 QBF 65 Quadratic character 110 Quadratic character, polynomial-time algorithm for 110 Quadratic equations in finite fields 145 189 Quadratic equations over finite fields 157 182 Quadratic nonresidues 109 110 189 Quadratic nonresidues, bounds for 123 253 372 Quadratic nonresidues, bounds for, assuming ERH 218—221 241 Quadratic nonresidues, bounds for, averaged 253—254 Quadratic nonresidues, bounds for, heuristics 217—218 242 245 Quadratic nonresidues, deterministic algorithm for 123 178 Quadratic nonresidues, efficient algorithm for finding 110
Реклама
 |
|
О проекте
|
|
О проекте