Авторизация
Поиск по указателям
Bach E., Shallit J. — Algorithmic Number Theory (том 1)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Algorithmic Number Theory (том 1)Авторы: Bach E., Shallit J. Аннотация: "[Algorithmic Number Theory] is an enormous achievement and an extremely valuable reference." — Donald E. Knuth, Emeritus, Stanford University
Язык: Рубрика: Математика /Теория чисел /Вычислительная теория чисел /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1996Количество страниц: 516Добавлена в каталог: 21.05.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Chailin, G.J. 315 Chang, T.-H. 195 Characteristic 0 34 Characteristic of a field 34 Characters 141 242 Characters on abclian group 144 Characters, Dinchlet 216 Characters, Dinchlet, primitive 216 Characters, Dinchlet, principal 216 Characters, orthogonality of 144 Characters, quadratic 141 142 146 195 196 Characters, sums over explicit bounds 234 Chartres, B.A 317 Chatland, H. 98 Chebotarev density theorem 231—263 Chebotarev density theorem, assuming GRH 231 Chebotarev density theorem, assuming GRH, explicit version 236 Chebotarev, N.G. 231 263 292 Chebyshev psi function 22 Chebyshev psi function for arithmetic progressions 235 Chebyshev psi function, estimates 246 367 Chebyshev theta function 22 246 Chebyshev theta function for arithmetic progressions 233 Chebyshev's inequality 356 Chebyshev, P.L. 204 208—209 236—238 245 246 261 367 368 Chemac, L. 1 Chen, C.-L. 354 Chen, J-N. 121 Chen, J.M. 196 Cheng, U. 149 Chernick, J. 304 313 380 Chernoff, H. 329 Cherwell, Lord 258 365 Chianilli, D.M. 10 16 Chicn, R.T. 196 Chin, Y.H 121 Chinese remainder theorem 3 101 104—108 118 122 289 Chinese remainder theorem for polynomials 136 152 Chinese remainder theorem in hardware 14 Chinese remainder theorem, algorithm for 105 Chinese remainder theorem, data structures interpretation 105 Chinese remainder theorem, generalized 106 122 Chinese remainder theorem, structure version 105 Chinese remainder theorem, systolic arrays and 122 Chistov, A.L. 197—199 245 379 Chor, В. 96 148 349 Chowla, S. 15 369 Chudnovsky, D.V. 16 Chudnovsky, G.Y 16 Church's thesis 12 Church, A. 12 16 Churchhouse, R.R. 14 248 CIPOLLA algorithm 157 373 Cipolla's algorithm 158 159 162 189 Cipolla, M. 157—158 162 189 194—196 199 314 353 360 367 373 Circuit families 58 65 Circulanls 144 Claasen, H.L. 152 Clark, D.W. 14 Clarke, J.H. 313 Class field theory 262 Class group 1 Class groups 260 262 263 Class groups, generating sets 263 Clause 48 Clausen, T. 309 310 co- 46 Cobham, A. 12 16 64 123 252 Coding scheme 46 Coding theory 148 167 Cody, W.F. 365 Cohen, A.M. 249 Cohen, G.L. 310 Cohen, H. xiv 1 11 13 14 285 316 369 385 Cohen, S.D. 152 199 255 Cohn, H. 15 260 262 376 Cohn, P.M. 96 98 CoIe, F.N. 15 Colbum, Z. 14 Collins, G.E. 10 63 97—99 123 149 152 347 377 Collins. S. 340 Colmar, Thomas de 6 Colquitt, W.N. 16 Comba, P.G. 63 Common divisor 19 Common multiple 19 Commutative law 30 Commutative rings 32 Complete residue system 139 Complex analysis xiii Complexity classes 45 46 Complexity classes, complement of 46 Complexity classes, parallel 57—59 Complexity classes, randomized 50—52 Complexity theory 41 44 Composite numbers 20 Composite pseudoprimes 313 COMPOSITES 46 Computation 53 Computation in 101 Computation in 102 Computation in 101 Computation in 101 Computation in 146 Computation in 146 Computation in 146 Computation in 146 Computation in finite fields, addition 132 Computation in finite fields, inverse 132 143 Computation in finite fields, multiplication 132 Computation in finite fields, subtraction 132 Computation in k[X], addition 132 Computation in k[X], division with remainder 132 Computation in k[X], multiplication 132 143 Computation in k[X], subtraction 132 Computational complexity 1 Computational complexity, number theory and 3—4 Computational number theory 2 Computational number theory, history of 4—11 Computer algebra 3 Comrie, L.J. 15 Condie, L. 310 317 Conductors 230 262 Conductors, estimates for 230 244 262—263 Conductors, examples of 230 Configuration 53 Conjectures, Artin 255—256 Conjectures, Bateman — Horn 259 Conjectures, Cramer 225 242 257 258 Conjectures, extended Riemann hypothesis 216 Conjectures, generalized Riemann hypothesis 229 Conjectures, Goldbach 1 259 Conjectures, Hardy and Littlewood 248 Conjectures, li(x) overestimates prime count 248 Conjectures, Mertens 248 Conjectures, pair correlation 250 257 Conjectures, Riemann hypothesis 211 Conjectures, strong prime tuples 226 243 248 258—259 Conjectures, twin prime 226 258 Conjectures, Wagstaff 224 256 Conjugacy classes in groups 31 Conjugate elements in groups 31 Conjugates 34 134 143 Conjunctive normal form 48 Conrey, J.B. 249 Continuants 73 74 77 98 Continuants, efficient computation of 75 Continuants, name of 98 Continued fraction algorithm, nearest-integer variation 79 Continued fractions 75—79 130 131 149 150 Continued fractions for rational functions 130—150 Continued fractions, algorithm for computing 76 Continued fractions, definition of 75 Continued fractions, generalization of 90 Continued fractions, higher-dimensional versions 98 Conway, J.H. 148 349 Cook reductions 64 Cook, B.M. 351 Cook, S.A. 12 16 63—65 96 327 329 Cooper, A.E. 123 Coppersmith, D. 2 13 352 Cormack. G.V 312 Cormen, T.H. xiii 328 Coset, right 30 Cosnard, M. 318 Costa Pereira, N. 263 Coster, M. 121 Cottrell, A. 121 Couffignal, L. 15 Couvreur, C. 310 Cramer's conjecture 242 Cramer, H. 225 241 242 246—249 256—258 375 Crandall, R.E. 2 13 258 312 Crepeau, C. 316 Critical strip 210 Cryptanalysis 149 Cryptography 4 148 cryptography, public-key 12 Cryptology 4 Cube roots in finite fields 182 Cubic equations over finite fields 184—185 193 Cubic nonresidues 183 Cull, P. 122 Cunningham chains 259 Cunningham Project 8 Cunningham tables 10 Cunningham, B.D. 196 Cunningham. A.J.C. 8 15 195 259 Curtze, M. 308 Cyclic groups 30 109 116 Cyclotomic fields 228 261 Cyclotomic fields, degree of 228 Cyclotomic fields, discriminant 228 Cyclotomic fields, discriminant of 261 Cyclotomic fields, integral basis 228 Cyclotomic polynomials 147 180 185 Cyclotomic polynomials, factorization mod p 147 Cyclotomic polynomials, irreducibility 261 Cyclotomic polynomials, polynomial factorization and 201 Cyclotomic polynomials, solution by radicals and 200 CYCLOTOMIC RINGS Test algorithm 290 Cyclotomif rings test 285—293 CZ algorithm 167 d'Ocagne, M. 15 D'ooge, M.L. 14 317 Dai, Z. 149 Damgard, I.B. 253 317 Datta, B. 98 121 Davenport, H. 98 246 251 252 263 319 Davenport, J.H. 314 361 387 Davida. G.I. 148 149 151 Davies, D. 252 261 Davis, J.A. 10 16 Davis, M. 12 16 17 371 Davis, P.J. 122 248 Davy, Sir H, 6 Daykin, D.E. 98 de Heinzelin, J. 245 de la Valtee Poussin, C.-J. 205 215 245 246 251 de Lagny, Т.E. 96 de Leeuw, K. 64 de Melo,W. 121 de Polignac, A. 258 Debnath, L. 14 Decision algorithms 47 Decision problems 44 45 Dedekind, J.W.R. 38 99 152 153 205 228 229 244 260—262 376 Degree of a field extension 33 Degree of a number field 227 Degree of a polynomial 32 Delay-line sieve 9 Deleglise, M. 300 318 365 Demeczky, M. 199 Demytko, N. 317 Deng, X. 96 Denjoy, A. 248 Denncau, M.M. 16 Depth 55 Depth of a boolean circuit 58 Depth of a straight-line program 57 Derivative 169 Deshouillers, J.-M. 2 13 Determinants, circulant 144 DETERMINISTIC SOLOVAY — STRASSEN algorithm 284 Di Porto, A. 314 352 Diab, M. 148 Diaconis, P. 335 Diamond, H.G. 246 Dick, T. xv Dickson, L.E. 14 15 122 196 258 260 309 310 313 352 382 Dictz. P.F. 385 Dietel, A. 121 Dieudonne, J. 39 Difference Engine 6 15 Different 260 Differentiation, asymptotic 367 Diffie, W. 12 Dijkstra, E.W. 311 Diophantine equations 3 45 Diophantine equations, unsolvahility of 12 Direct product of groups 31 Direct sum of rings 33 Directed graph 57 Dirichlet divisor problem 39 Dirichlet series, convergence region 239 Dirichlet's theorem 152 Dirichlet, P.G.L. 39 93 215 221 245 251 322 332 348 351 372 Discrete logarithms 161 196 Discrete logarithms, baby-step giant-step method 161 Discriminants 260 Discriminants of cyclotomic fields 261 Discriminants of elements 244 Discriminants of number fields 227—228 244 260 Discriminants of number fields, intractability 245 Discriminants of polynomials 119 Discriminants of quadratic fields 245 Discriminants, estimates for 244 260—261 Discriminants, ramified primes and 262 Discriminants, relative 260 Distinct degree algorithm 171 198 Distinct-degree factorization 171 191 198 Distributed computation 16 Division rings 32 Division, fast algorithms for 60 divisors 19 Divisors for polynomials 194 Divisors, number of 26 35—36 319 Divisors, product of 37 Divisors, sum of 22 35 319 Dixon, J.D. 11 97 310 316 dle Moivre, A. 330 Dobkin, D. 121 Doenias, J. 312 Dornsetter, J.L. 149 Downey, P. 121 Drake, S. 14 Dresel, L.A.G. 314 Dress, F. 2 13 Driscoll, J. 99 332 344 356 du Bois-Reymond. P. 39
Реклама
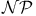
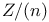, addition ![$\mathbb{Z}/(n)[X]/(f)$](/math_tex/fda1db55a60e5676ec8caf17d24d3aad82.gif)
, addition 
|
|
О проекте