|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grimaldi R.P., Rothman D.J. — Discrete and Combinatorial Mathematics: An Applied Introduction |
|
|
 |
| Предметный указатель |
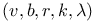 -design 825 826 831 -design 825 826 831
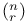 15 21 41 42 436 15 21 41 42 436
 422 422
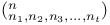 23 23
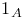 279 279
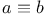 (mod n) 686 (mod n) 686
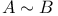 A-23 A-23
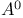 , , 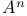 , , 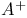 , A* 315 , A* 315
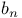 , the n-th Catalan number 38 490 , the n-th Catalan number 38 490
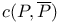 646 646
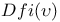 616 619—621 616 619—621
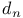 402 403 410 402 403 410
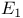 , , 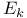 , E 371 , E 371
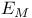 374 374
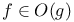 290 291 290 291
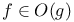 on S 5 498 on S 5 498
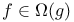 293 293
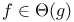 294 294
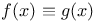 (mod s(x)) 808 (mod s(x)) 808
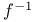 283 283
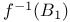 285 285
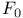 (contradiction) 53 (contradiction) 53
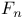 719 734 719 734
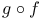 280 280
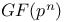 830 830
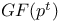 813 818 813 818
 626 626
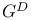 549 549
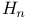 (the nth harmonic number) 202 (the nth harmonic number) 202
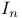 348 A-16 348 A-16
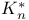 559 559
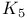 540 543 540 543
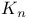 352 523 352 523
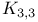 542 543 542 543
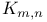 541 541
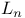 (the nth Lucas number) 216 (the nth Lucas number) 216
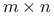 matrix A-11 matrix A-11
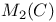 , , 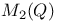 , , 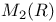 , , 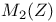 674 674
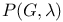 566—568 570 566—568 570
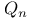 532 542 667 532 542 667
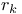 , , 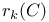 405 406 405 406
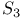 , , 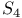 750 750
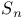 787 789 794 830 787 789 794 830
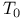 (tautology) 53 (tautology) 53
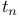 (the nth triangular number) 198 (the nth triangular number) 198
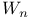 520 572 520 572
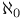 (aleph null) 303 A-30 A-31 (aleph null) 303 A-30 A-31
 457 458 469 457 458 469
![$\beta [=(1-\sqrt{5})/2]$](/math_tex/eeba96a544609853661c914dc2db25bc82.gif) 457 457
 (blank, space) 311 (blank, space) 311
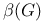 564 666 564 666
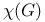 565 621 565 621
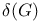 664 665 664 665
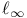 827 828 827 828
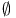 (the null set) 127 (the null set) 127
 88 88
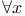 88 124 88 124
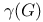 577 577
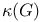 517 549 615 517 549 615
 (for a design) 826 (for a design) 826
 (the empty string) 310 323 (the empty string) 310 323
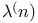 567 567
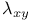 825 825
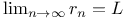 103 103
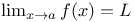 99 100 99 100
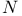 133 133
 , , 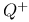 , , 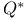 133 133
 , , 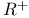 , , 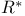 133 134 133 134
 , , 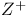 133 134 133 134
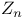 134 686 134 686
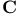 , , 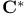 134 134
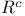 (converse of relation (converse of relation 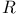 ) 282 ) 282
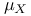 177 177
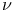 320 320
 (output function) 320 (output function) 320
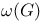 293 293
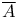 138 138
 (Euler’s phi function) 394 395 689 692 747 759 760 (Euler’s phi function) 394 395 689 692 747 759 760
 notation 239 notation 239
 notation 17 notation 17
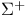 , , 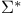 310 310
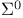 , ,  , , 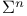 309 309
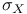 (standard deviation) 180 182 183 (standard deviation) 180 182 183
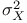 (variance) 180 (variance) 180
 294 294
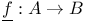 252 252
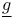 dominates f on S 498 dominates f on S 498
(0, 1)-matrix 345 347 348 352 378 see
(i,j)-entry of a matrix A-1 1
(m + 1, m) parity-check code 764 765
(n, m) block code 764 see
1-equivalence 338
1-equivalent states (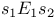 ) 371 ) 371
2-isomorphic graphs 555
2-methyl propane 584
a is congruent to b modulo n 686
a-z cut 645
Abel, Niels Henrik 705 745 794 830
Abelian group 161 745 746 799
Absolute value 219 224
Absorption Laws for a Boolean algebra 735
Absorption Laws for Boolean functions 713
Absorption Laws for Boolean variables 713
Absorption Laws for logic 59
Absorption Laws for set theory 139
Abstract algebra 394 624 742
Access function 254
Achilles 119
Ackermann, Wilhelm 259
Ackermann’s function 259
Acronym 155
Aczel, Amir D. 706 708
Addition 136 137
Addition of binary numbers 720
Addition of equivalence classes of integers (in 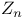 ) 687 ) 687
Addition of equivalence classes of polynomials 809
Addition of matrices A-12
Addition of polynomials 800
Additions 636 637
Additive identity for a ring 674
Additive identity for matrices A-13
Additive identity for real numbers 103
Additive inverse for a ring element 674 679 680 701
Additive inverse for integers 278
Additive inverse for matrices A-13
Additive inverse for real numbers 103
additive rule 162 168 172
Address in a universal address system 589
Address in computer memory 5 694
Address, class A address 12
Address, class B address 12
Address, class C address 12
Address, internet address 12
Address, local address 12
Adjacency list 379
Adjacency list representation 378 379
Adjacency matrix (for a graph) 352 539 600
Adjacency of a pair of vertices 352
Adjacent from 349 514
Adjacent mark ordering algorithm 453 506
Adjacent to 349 514
Adjacent vertices 349
Adleman, Leonard 759
Affine Cipher 691 692 759
Affine plane 820—822 826—828 831
Aggregate 123
Aho, Alfred V. 378 506 507 574 575 623 624 642 667 668 708
Ahuja, Ravendra K. 562 575 637 643 654 668
Al-jabr 242
Al-Khowarizmi, Abu Ja’far Mohammed ibn Musa 242
| Albert, A. Adrian 831
Aleph 303
alfa 226
Algebra 123 242
Algebra of logic 742
Algebra of propositions 55 57 58 see
Algebra of switching circuits 742
Algebra of switching functions 711
Algebraic coding theory 18 761—779 795 796
Algebraic coding theory, (m + 1, m) parity-check code 764 765
Algebraic coding theory, (n, m) block code 764
Algebraic coding theory, binary representations 778 779
Algebraic coding theory, binary symmetric channel 762 763
Algebraic coding theory, block code 764
Algebraic coding theory, code word 763 769 771 772 774 776—778
Algebraic coding theory, coding schemes 763
Algebraic coding theory, coset leader 775—777
Algebraic coding theory, d(x, y) 766
Algebraic coding theory, decoding 763
Algebraic coding theory, decoding algorithm 772
Algebraic coding theory, decoding by coset leaders 776
Algebraic coding theory, decoding function 764 767
Algebraic coding theory, decoding scheme 769
Algebraic coding theory, decoding table 774 775
Algebraic coding theory, decoding table with syndromes 776
Algebraic coding theory, distance 766
Algebraic coding theory, distance function 766 767
Algebraic coding theory, dual code 773
Algebraic coding theory, efficiency of a coding scheme 764
Algebraic coding theory, encoding 763
Algebraic coding theory, encoding function 763 764 767 769 771 773
Algebraic coding theory, equivalent codes 778
Algebraic coding theory, error 762
Algebraic coding theory, error correction 767—769
Algebraic coding theory, error detection 767—769
Algebraic coding theory, error pattern 762 763 771 779
Algebraic coding theory, five-times repetition code 765 769
Algebraic coding theory, generator matrix 769 771 772 774 111
Algebraic coding theory, Gilbert bound 773
Algebraic coding theory, Golay, Marcel 761 795 796
Algebraic coding theory, group code 773 774 776 111
Algebraic coding theory, Hamming bound 773
Algebraic coding theory, Hamming code 778
Algebraic coding theory, Hamming matrix 778
Algebraic coding theory, Hamming metric 767
Algebraic coding theory, Hamming, Richard 761 766 795 796
Algebraic coding theory, independent events 762
Algebraic coding theory, majority rule 765
Algebraic coding theory, message 763 769 777 778
Algebraic coding theory, minimum distance between code words 767—769 771 773 774
Algebraic coding theory, minimum weight of nonzero code words 774
Algebraic coding theory, mixed strategy 768
Algebraic coding theory, multiple errors 763
Algebraic coding theory, nearest neighbor 771
Algebraic coding theory, noise 761
Algebraic coding theory, parity-check code 764 765
Algebraic coding theory, parity-check equations 770 111
Algebraic coding theory, parity-check matrix 772 774 776—779
Algebraic coding theory, probability 761—765
Algebraic coding theory, rate of a code 764 778
Algebraic coding theory, received word 762 763 111
Algebraic coding theory, retransmission 765 769
Algebraic coding theory, S(x,k) 161
Algebraic coding theory, Shannon, Claude Elwood 761 795 797
Algebraic coding theory, sphere (S(x,k)) 767
Algebraic coding theory, syndrome 771 775—777 779
Algebraic coding theory, systematic form 778
Algebraic coding theory, transmission error 762 767
Algebraic coding theory, triangle inequality 767
Algebraic coding theory, triple repetition code 765 768 769
Algebraic coding theory, weight 766
Algebraic coding theory, wt(x) 766
Algebraic expression 590
Algebraic formulae 623
Algebraic structures 745 761
Algebraic substitution 449
Algorism 242
Algorithm 41 42 233 242—244 289 290 294 295 297 299—301 349 378 442 599 605 613 615 619—621 624 632 633 636—642 649 653
Algorithmic manner 631
Algorithms, adjacent mark ordering 458 506
Algorithms, articulation points 619 620
Algorithms, biconnected components 619 620
Algorithms, binary search 501—503
Algorithms, breadth-first search 598 599
Algorithms, bubble sort 450
Algorithms, decoding 772
Algorithms, depth-first search 597 598 617
Algorithms, Dijkstra’s shortest-path 633 634 667 668
Algorithms, divide-and-conquer 496—503
Algorithms, Edmonds — Karp algorithm 653—657 663
Algorithms, Euclidean algorithm for integers 232 233
Algorithms, Euclidean algorithm for polynomials 808
Algorithms, exponentiation 297—299
Algorithms, Fibonacci numbers 477 478
Algorithms, Ford — Fulkerson algorithm 654—657 663
Algorithms, generating permutations 453 506
Algorithms, greatest common divisor 232 233
Algorithms, greatest common divisor (recursive) 455
Algorithms, Huffman tree 613
Algorithms, Kruskal’s algorithm 639—641
Algorithms, linear search 296 302
Algorithms, maximum value 301
Algorithms, Merge Sort 496 608
Algorithms, merging two sorted lists 607
Algorithms, minimization process for a finite state machine 372—373
Algorithms, nonisomorphic trees on n labeled vertices 586 587
Algorithms, polynomial evaluation 301
Algorithms, Priifer code for a labeled tree 586 587
Algorithms, Prim’s algorithm 641—643 668
Algorithms, searching an array 295 296
Algorithms, topological sorting algorithm 360 361
Algorithms, universal address system 589
Alkane 584
Allowable choices 87
alpha testing 185
Alphabet 18 309—311 313 315 316 337 338 609 610
Alphabetical ordering 589
Alternating sequence 650
Alternating triple 135
Alternative form of the Principle of Mathematical Induction 206—208 217 238 298 458 503 582 583
American Journal of Mathematics 411
American National Standards Institute 125
An Investigation in the Laws of Thought on Which Are Founded the Mathematical Theories of Logic and Probability 119
An Investigation of the Laws of Thought 186 711 742
Analysis 444
Analysis of Algorithms 3 247 259 292 294—300 304 305 453 473 503 A-1 A-6
Analytic Theory of Probability 150 188
Analytical engine 242
Analytische Zahlentheorie 304
Ancestor 588 616—619
AND 48 50
AND gate 149 719 720
Annals of Mathematics 706
ANSI FORTRAN 125
Antichain 381
Antisymmetric property (of a relation) 340 341 347 348 353 357 358 376 377
Anton, Howard A-21
AP(F) 822 824 826—828
Apianus, Petrus 188
Appel, Kenneth 565 573 575
Application Specific Integrated Circuit 149
Applied Boolean algebra 742
Approximately equal ( ) 7 ) 7
Approximation theory 304
arbitrary 110
ARC 321 329 349 514
Argue by the converse 74 82 109 547
Argue by the inverse 75 82 110
Argument 47 53 67 72 74 75 107 108 112
Aristotle 117 118 238
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



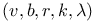 -design
-design 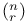

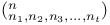
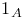
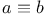 (mod n)
(mod n) 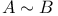
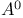 ,
, 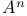 ,
, 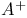 , A*
, A* 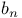 , the n-th Catalan number
, the n-th Catalan number 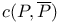
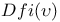
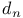
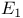 ,
, 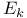 , E
, E 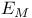
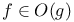
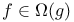
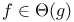
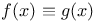 (mod s(x))
(mod s(x)) 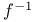
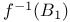
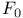 (contradiction)
(contradiction) 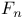
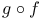
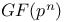
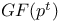

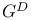
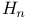 (the nth harmonic number)
(the nth harmonic number) 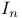
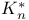
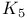
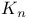
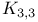
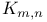
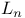 (the nth Lucas number)
(the nth Lucas number) 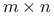 matrix
matrix 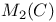 ,
, 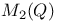 ,
, 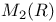 ,
, 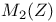
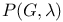
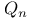
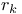 ,
, 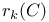
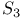 ,
, 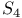
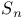
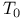 (tautology)
(tautology) 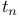 (the nth triangular number)
(the nth triangular number) 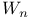
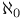 (aleph null)
(aleph null) 
![$\beta [=(1-\sqrt{5})/2]$](/math_tex/eeba96a544609853661c914dc2db25bc82.gif)
 (blank, space)
(blank, space) 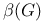
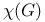
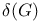
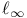
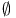 (the null set)
(the null set) 
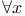
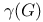
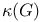
 (for a design)
(for a design) 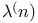
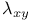
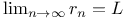
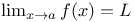
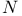
 ,
, 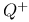 ,
, 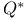
 ,
, 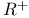 ,
, 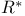
 ,
, 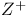
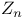
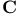 ,
, 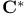
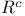 (converse of relation
(converse of relation 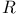 )
) 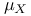
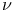
 (output function)
(output function) 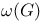
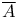
 (Euler’s phi function)
(Euler’s phi function)  notation
notation  notation
notation 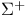 ,
, 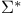
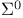 ,
, 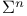
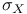 (standard deviation)
(standard deviation) 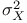 (variance)
(variance) 
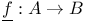
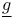 dominates f on S
dominates f on S 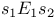 )
)  )
)