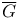|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grimaldi R.P., Rothman D.J. — Discrete and Combinatorial Mathematics: An Applied Introduction |
|
|
 |
| Предметный указатель |
Finite state machine, internal states 320 321 327 371
Finite state machine, k-equivalent states 338 371
Finite state machine, k-unit delay machine 329
Finite state machine, Mealy machine 333
Finite state machine, minimization process 371—376 378
Finite state machine, next state 320
Finite state machine, next state function 320
Finite state machine, one-unit delay machine 329
Finite state machine, output 320—322 324 328 329
Finite state machine, output alphabet 320 321
Finite state machine, output function 320
Finite state machine, pigeonhole principle 327
Finite state machine, reachability 338
Finite state machine, reachable state 330
Finite state machine, redundant state 371 373
Finite state machine, reset 321
Finite state machine, second level of reachability 338
Finite state machine, sequence recognizer 326 327 332
Finite state machine, serial binary adder 323 324
Finite state machine, sink (state) 331
Finite state machine, starting state 320 329
Finite state machine, state diagram 321 324 327
Finite state machine, state table 321 322 324 331
Finite state machine, strongly connected machine 331
Finite state machine, submachine 331
Finite state machine, transfer sequence 331
Finite state machine, transient state 330
Finite state machine, transition sequence 331
Finite state machine, transition table 321
Finite state machine, two-unit delay machine 329
Finite strings 310
Finite three-dimensional geometry 831
Finizio, Norman 506 507
First level of infinity 303 A-30
First level of reachability 338
First-degree factor 805 806
First-in first-out structure 598
First-order linear recurrence relations 448 450
Fisher, R.A. 831
Fissionable material 486
Five-times repetition code 765 769 see
Fixed (invariant) 781 783 789
Fixed order 597
Fixed point (of a function) 403
Flach, Matthias 706
Floor function (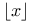 ) 253 254 297 496 602 ) 253 254 297 496 602
Flow in a transport network 644—654 656 662 663
Flow of current 536
flowchart 203 204 349
Folding method (for hashing) 694
Fontane, Johnny 186
For all x 88
For any x 88
For at least one x 88
For each x 88
For every x 88
For some x 87 88
Forbidden positions 406 408
Ford — Fulkerson algorithm 654—657
Ford, Lester Randolph, Jr. 649 653 654 668 669
Foreign Office at Bletchley Park 333
Forest 581 639 641 642
Formal Logic; or, the Calculus of Inference, Necessary and Probable 118
Formulario Mathematico 243
Forward edge 650 651 654 655
Foulds, L.R. 562 575 576
Foundations of mathematics 333
Foundations of the Theory of Probability 188
Founder of information theory 795
Four-color conjecture 573
Four-color problem 565 575
Fourier, Joseph Baptiste Joseph 303
Foxtrot 226
Fractals 506
Free variable 88
Frege, Gottlieb 119
Frequency of occurrence 611 692
Frey, Gerhard 706
Frobenius, Georg 796
Front (of a list) 598 599
Fulkerson, Delbert Ray 649 653 654 668 669
Full binary tree 611
Full house 152
Full m-ary tree 614
full-adder 721
Function 99 175 186 211 247 252—257 259—263 267—271 278—293 295 302 303 309 311 318 320 376 394 395 403 409 410 602 644 660 673 697—704 712 739
Function complexity 247
Function composition see "Composite function"
Function dominance 292 294 341 498
Function inverse see "Inverse of a function"
Function, 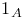 279 279
Function, 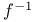 283 283
Function, access function 254
Function, Ackermann’s function 259
Function, associative binary operation 268
Function, Big-Oh notation 290
Function, bijective function 279 283
Function, binary operation 267—269
Function, Boolean function 712
Function, ceiling function 254
Function, characteristic function 307
Function, closed binary operation 267 268 270
Function, codomain 253 279 281 287
Function, commutative binary operation 268 270
Function, composite function 280 281
Function, composition of functions 278 280 282
Function, constant function 261
Function, decoding 767
Function, definition 252
Function, distance function 766 767
Function, domain 175 253 257 270 281 287
Function, dominance 292—294
Function, encoding 763 764 767 769 771 773
Function, equality 279
Function, Euler’s phi function 394 395 689
Function, exponential 402 A-1 A-5
Function, extension 257
Function, finite function 247 284 302
Function, finite sequence of n terms A-25
Function, fixed point 403
Function, floor function 253 254 297
Function, function complexity 247
Function, function dominance 290—292 294 498
Function, greatest integer function 253 297
Function, hashing function 673 694 695 708
Function, identity function 279
Function, image of a set 256 257
Function, image of an element 253
Function, incompletely specified Boolean function 732
Function, infinite sequence A-25
Function, injective function 255
Function, inverse function 278 283 285 A-9
Function, invertible function 282—285 287
Function, logarithmic A-1 A-5
Function, mapping 252
Function, monary operation 267
Function, monotone increasing function 494 495 500 501 503 608 609
Function, next state function 320 682
Function, notation 253
Function, one-to-one correspondence 279 303
Function, one-to-one function 255—257 409 410
Function, onto function 260—263 265
Function, order (of a function) 290 292 293
Function, order-preserving function 366 509
Function, output function 320 682
Function, partial function 260
Function, phi function 394 395
Function, powers of a function 282
Function, pred (predecessor) 307
Function, preimage of a set 285—287
| Function, preimage of an element 253
Function, projection 270 271
Function, range 253
Function, recursive function 453
Function, restriction 257
Function, scattering function 694 708
Function, self-dual Boolean function 744
Function, sequence 255
Function, space complexity function 290
Function, succ (successor) 307
Function, surjective function 260
Function, switching function 712
Function, symmetric Boolean function 744
Function, time complexity function 290 297—299
Function, trunc(ation) 254
Function, unary operation 267 268
Fundamental conjunction 715—718 721 723 724 732 738
Fundamental disjunction 717 718
Fundamental theorem of algebra 356
Fundamental Theorem of Arithmetic 193 237—240 244 254 265 275 314 342 394 703 704 A-29
F[x] 802
F[x]/(s(x)) 810
G 523
g dominates f 290
G-e (e an edge) 522
G-v (v a vertex) 522
Galileo 303
Gallian, Joseph A. 707 708 795 796
Gallier, Jean H. 119 120
Galois field 813 818
Galois theory 707 795 831
Galois, Evariste 707 794 795 813 830 831
Gambler’s ruin 510
games of chance 188
Gardiner, Anthony 795 796
Gardner, Martin 39 42 507 795 796
Garland, Trudi Hammel 506 507
Garrett, Paul 693 708 795 796
Gate 720
Gating network 309 719—722 731
Gauss, Carl Friedrich 377 705 707
gcd (greatest common divisor) for integers 231—236 240 394 453 454 688 734 737
gcd (greatest common divisor) for polynomials 807 808
General solution of a homogeneous recurrence relation 468
General solution of a nonhomogeneous recurrence relation 471
General solution of a second-order linear homogeneous recurrence relation with constant coefficients 456
Generalizations of the principle of inclusion and exclusion 397—401
Generalized associative law for 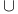 213 213
Generalized associative law for 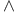 212 212
Generalized associative law for a group 746
Generalized associative law of addition of real numbers 214—216
Generalized associative law of multiplication of real numbers 214 215
Generalized associative laws in a ring 674
Generalized Binomial Theorem 422
Generalized DeMorgan’s laws 146
Generalized distributive laws in a ring 674
Generalized intersection of sets 146
Generalized union of sets 146
Generated recursively A-26
Generates 753
Generating function 303 415—445 452 482—487 489 505 783 790 791
Generating function in solving recurrence relations 482—487
Generating function, calculational techniques 418—431
Generating function, convolution of sequences 430 431 440
Generating function, definition 418
Generating function, distributions 415—417
Generating function, exponential generating functions 436—439 443
Generating function, geometric series 419
Generating function, moment generating function 443 444
Generating function, nonlinear recurrence relation 487—490
Generating function, ordinary generating function 436
Generating function, partitions of integers 432—435
Generating function, power series 417
Generating function, rook polynomial 416
Generating function, summation operator 440—442
Generating function, table of identities 424
Generator matrix 769 771 772 774 777 see
Generator of a cyclic group 755
GENERIC 110
Genesereth, Michael R. 119 120
Geometric progression 447
Geometric random variable 430 446
Geometric series 419 423 428 476
Geometrie die Lage 622
Geometry 123 222 242 506 794 795
Gerasa 707
Germain, Sophie 705
Gersting, Judith L. 333 334
GF 813
GF(n) 821 824 827 828
Gilbert bound 773 see
Gill, Arthur 333 334
Giornale di matematiche 820
glb (greatest lower bound) 363 709
Global result 632 639
Goedel, Kurt 187
Goedel’s Proof 188
Golay, Marcel J.E. 761 795 796
Goldberg, Samuel 506 507
Golden ratio 457 469 506
Golomb, Solomon W. 796
Gone With the Wind 47 48 52
Gopolan, K. Gopal 743
Gorenstein, Daniel 795 796
Graceful (labeling of a tree) 627 628
Graff, Michael 795
Graham, Ronald Lewis 304 305 506 507 642 667—669
Grandparent 593
Graph coloring 564—573 575
Graph isomorphism 523 526—528 699
Graph planarity 352 615
Graph theory 324 349—354 378 379 395 396 411 513—579 615—621 624 631 632 657 659—665 667 730 see "Transport "Trees"
Graph theory in degree (of a vertex) 535
Graph theory,  626 626
Graph theory, 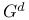 549 549
Graph theory, 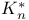 559 559
Graph theory, 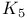 540—543 547 540—543 547
Graph theory, 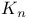 352 523 352 523
Graph theory, 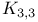 542 543 547 542 543 547
Graph theory, 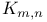 541 541
Graph theory, 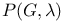 566—568 570 566—568 570
Graph theory, 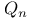 532 542 667 532 542 667
Graph theory, 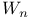 520 572 520 572
Graph theory, 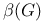 , the independence number of G 564 666 , the independence number of G 564 666
Graph theory, 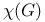 , the chromatic number of G 565 621 , the chromatic number of G 565 621
Graph theory, 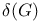 664 665 664 665
Graph theory, 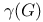 , the domination number of G 577 , the domination number of G 577
Graph theory, 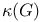 , the number of components of G 517 549 615 , the number of components of G 517 549 615
Graph theory, 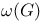 , the clique number of, G 578 , the clique number of, G 578
Graph theory, 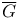 523 523
Graph theory, 2-isomorphic graphs 555
Graph theory, adjacency list 379
Graph theory, adjacency list representation 378 379
Graph theory, adjacency matrix 352 539 600
Graph theory, adjacent from 349 514
Graph theory, adjacent to 349 514
Graph theory, adjacent vertices 349
Graph theory, algorithm for articulation points 619 620
Graph theory, arc 349 514
Graph theory, articulation point 615—621 624
Graph theory, associated undirected graph 350 353 517
Graph theory, biconnected component 615 619—621 624
Graph theory, biconnected graph 615
Graph theory, binary tree 488 595 600
Graph theory, bipartite graph 541 542 558 659 660 662—665 668
Graph theory, bridge 550
Graph theory, chromatic number 413 565 615 621
Graph theory, chromatic polynomial 413 564—571 574
Graph theory, circuit 516 534 551
Graph theory, clique 578
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



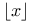 )
) 
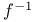
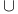
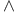

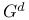
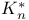
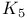
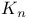
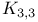
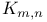
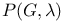
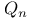
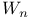
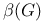 , the independence number of G
, the independence number of G 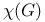 , the chromatic number of G
, the chromatic number of G 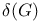
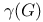 , the domination number of G
, the domination number of G 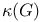 , the number of components of G
, the number of components of G 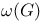 , the clique number of, G
, the clique number of, G