|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grimaldi R.P., Rothman D.J. — Discrete and Combinatorial Mathematics: An Applied Introduction |
|
|
 |
| Предметный указатель |
STIRLING, JAMES 303
Stirling’s formula 304
Stoll, Robert R. 119 120
Storage circuits 5
Strang, Gilbert A-21
Street, Anne Penfold 796 797 831 832
String 12 18 19 128 129 309—323 328 337 338 609 610 761
String,  (the empty string) 310 323 (the empty string) 310 323
String, concatenation 311 312
String, empty string 310 323
String, equality of strings 311
String, length of a string 18 310—312
String, palindrome 319
String, powers of strings 312
String, prefix 312 313 315
String, proper prefix 312 315
String, proper substring 313
String, proper suffix 312
String, reversal 317 319
String, substring 313 315 328 338
String, suffix 312 313 315
Strongly connected component 352
Strongly connected directed graph 351 539
Strongly connected machine 331
Structured programming 203
Subboard 404 405 408 409
Subfield 809 811 812
Subgraph 521 523 525 582 588
Subgraph induced by a set of vertices 522
Subgroup 748 749 756—758
Subgroup generated by a group element 754
Sublist 450 606 607
Submachine 331 682
Subring 682—684 699 702
Subsections of strings 312
Subsequence A-26
Subset 124—128 130—132 138 140 141 149
Subset relation 250 358 359 362 363 737
Subsets with no consecutive integers 457
Substitution rules (in logic) 60—62 69 71 72 76 80
Substring 313 315 328 338
Subtraction 137 224 225 227 228 356
Subtraction (in a ring) 680
Subtree 488 583 588 590 593—596 602
Succ (successor) function 307
Success 161 178 179 182
Successor 243 307
Such that 124
Sufficient condition 48
Suffix 312 313 315 338
Suffix function 318
Sum of a geometric series 476
Sum of atoms 738
Sum of bits 720 721
Sum of Boolean functions 712
Sum of matrices A-12
Sum of minterms 717
Sum of squares 200
Sum of the weights of the edges 631
Summation 17 18
Summation formulas 32 33 35 47 196 197 200 259 430 441 470
Summation notation 17 18
Summation operator 440 441
Summation, index 17
Summation, lower limit 17
Summation, upper limit 17
Summations 292
Sumo wrestlers 277
Sun (R) Microsystems, Inc. 5
Superimposed 815
Superset 138
Suppes, Patrick C. 189
Surjective function 260
Switches (in a network) 64—66 551
Switches in series 65
Switching circuits 742
Switching function 711 712 719 742
Switching network 64—66
Sylow, Ludwig 795
Sylvester, James Joseph 411 A-11
Symbolic logic 118
Symmetric Boolean function 744
Symmetric difference 136 313
Symmetric group (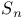 ) 787 789 794 830 ) 787 789 794 830
Symmetric property (of a relation) 339—343 347 348 353 366—369 376 377
Syndrome 771 775—777 779 see
Syndrome decoding 779
System of congruences 702 707 708
System of distinct representatives 663 668
System of linear equations A-18 A-19
System of recurrence relations 486 487
Systematic form 778 see
Szekeres, George 276
T-shaped figure 121
Table for a relational data base 271
Table for decoding 774—776 see
Table of Big-Oh forms 293
Table of identities for generating functions 424
Table of particular solutions for the method of undetermined coefficients 479
Table of rules for negating statements with one quantifier 96
Table of rules of inference 78
Table of Stirling numbers of the second kind 264
Tabular form 71
Tabulation algorithm 742
Tallahassee 17
Taniyama, Yutaka 706
Tarry, G. 819
Tartaglia, Niccolo 188
Taubes, G. 795 797
Tautology 53 58—61 67 69 71 76 113
Taylor, Richard 706
Telephone communication system 320
Terminal (in a switching network) 64
Terminal vertex 588
Terminals 552
Terminating vertex 349 514
Terminus 349 514
Ternary operation 306
Ternary strings 469
tetrahedron 547 548 792
Thatcher, Margaret 74
The Book of Creation (Sefer Yetzirah) 41
The Calculus of Inference, Necessary and Probable 118
The Godfather 186 692
The Mathematical Analysis of Logic, Being an Essay towards a Calculus of Deductive Reasoning 118
Theorem 53 67 70 84 87 98 99 105 106 110 112 113 117 119 193 222
Theorie Analytique des Probabilites 443
Theory of equations 411
Theory of graphs see "Graph theory"
Theory of groups see "Group theory"
Theory of languages 18 332 337
Theory of matrices 411
Theory of numbers see "Number theory"
Theory of rings see "Ring theory"
Theory of sets see "Set theory"
Theory of types 187
There exists an x such that 88
Therefore ( ) 71 ) 71
Third Reich 333
Third-order linear homogeneous recurrence relations with constant coefficients 463 464
Thomas, R. 575 576
Thompson, John 795
Tile 470
Tiling 464
Time complexity function 290 297—299 450 452 496 498 500 501 605—609 624 see
Time complexity function for the bubble sort 450—452
Time complexity function for the merge sort 607—609
Tolerance 650
Top (of a stack) 490
Top-down approach 41
| Topological sorting 359 377
Topological sorting algorithm 360 361 363
Total order 359—361 377
Totally ordered poset 359
Tournament 559 602
Towers of Hanoi 472 505
Trail 516 517 528
Transfer sequence 331
Transfinite cardinal number 303
transform 253
Transformation 36 37
Transient state 330
Transition 320
Transition sequence 331
Transition state 321
Transition table 321
Transitive property (of a relation) 339—343 347 348 353 357 358 366—368 376 377
Transmission errors 762 767
Transmission of digital signals 188
Transmitter 767 769
Transport network 324 644—658 660—663 665 667 668
Transport network, 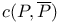 646 648 652 654 646 648 652 654
Transport network, a-z cut 645
Transport network, associated undirected graph 645 650
Transport network, backtrack 653 656
Transport network, backward edge 650 651 654
Transport network, capacity 644
Transport network, capacity for a vertex 657
Transport network, capacity of a cut 646 665
Transport network, capacity of an edge 644 645 650 654
Transport network, chain 650
Transport network, conservation condition 645 651
Transport network, cut 645—648 652 661 662
Transport network, definition 644
Transport network, Edmonds — Karp algorithm 653—657
Transport network, f-augmenting path 650—654 656 663
Transport network, flow in a network 644—654
Transport network, Ford — Fulkerson algorithm 654—657
Transport network, forward edge 650 651 654 655
Transport network, Max-Flow Min-Cut Theorem 649 652
Transport network, maximal flow 645 647
Transport network, network 644
Transport network, quasi-path 650
Transport network, saturated edge 645 649 650
Transport network, semipath 650—653
Transport network, sink 644—646 648 653
Transport network, source 644—646 648 653
Transport network, tolerance 650
Transport network, unsaturated edge 645
Transport network, usable edge 653 655 656
Transport network, val(f) 645—648
Transport network, value of a flow 645—649 651—653
Transpose of a matrix 348
Transposition of a Ferrers graph 435
Trappe, Wade 693 708 795 797
Traveling salesman problem 562 574
Treatise on Algebra 186
TREE 250 488 489 573 581—629 641 642 653 655 656 796 see
Tree diagram 154 157 248—250 331 488
Tree traversal 594
Tree, algorithm for articulation points 619 620
Tree, algorithm for constructing a Huffman tree 613
Tree, algorithm for counting labeled trees 586 587
Tree, algorithm for the universal address system 589
Tree, ancestors 588 616—619
Tree, articulation point 615—621 624
Tree, back edge 616—619 621
Tree, backtrack(ing) 593 596—598 600 616
Tree, balanced tree 601 602
Tree, biconnected component 615 619—621 624
Tree, binary rooted tree 589 590 594 595
Tree, binary tree 488 595 600
Tree, branch nodes 588
Tree, branches 488 614
Tree, breadth-first search 598—600
Tree, breadth-first search algorithm 598 599
Tree, breadth-first spanning tree 599
Tree, caterpillar 627 628
Tree, characteristic sequence 625
Tree, child 588 590 594 598 617—620
Tree, complement of a subgraph 586
Tree, complete binary tree 589 595 596 600 605
Tree, complete binary tree for a set of weights 612
Tree, complete m-ary tree 600—602
Tree, complete ternary tree 603
Tree, decision tree 602 603
Tree, definition 581
Tree, depth-first search 597 598 600 617 624
Tree, depth-first search algorithm 597 598 617
Tree, depth-first spanning tree 615—620
Tree, descendants 588 616—619
Tree, dfi(v) 616 619—621
Tree, dictionary order 589
Tree, directed tree 587
Tree, Fibonacci tree 626
Tree, forest 581 639 641 642
Tree, full binary tree 611
Tree, full m-ary tree 614
Tree, graceful tree 627
Tree, grandparent 593
Tree, height 601—603 611
Tree, Huffman tree 613 614
Tree, inorder (traversal) 594 595
Tree, internal vertices 588 591 593 601 612
Tree, Kruskal’s algorithm 639—641
Tree, labeled complete binary tree 610
Tree, labeled tree 586
Tree, leaf 588
Tree, left child 590 594 610 611
Tree, left subtree 590 592 594—596
Tree, level 588 589 593 597 607 611
Tree, level number 588 601 602 612
Tree, lexicographic order 589
Tree, m-ary tree 600
Tree, merge sort algorithm 496 608
Tree, minimal spanning tree 639 667 668
Tree, null child 594 595
Tree, optimal spanning tree 638 639 642
Tree, optimal tree 612 613 640—642
Tree, order for the vertices of a tree 588 589 592—595
Tree, ordered binary tree 488
Tree, ordered rooted tree 588
Tree, parent 588 593 597 613 619—621
Tree, pendant vertex 583 584
Tree, postorder (traversal) 592—595
Tree, prefix code 609 611 613 614 624
Tree, preorder (traversal) 592—596
Tree, Prim’s algorithm 641—643 653
Tree, quick sort 609
Tree, right child 590 594 610 611
Tree, right subtree 592 594—596 614
Tree, root 587—590
Tree, rooted Fibonacci tree 626
Tree, rooted tree 587—596 600 601
Tree, sibling 588 593 612
Tree, sorting 581 605 606 608
Tree, spanning forest 582
Tree, spanning tree 582 596 597 599 631 638 640
Tree, spine (of a caterpillar) 627 628
Tree, subtrees 583 588 590 593—596 602
Tree, terminal vertex 588
Tree, universal address system 589
Tree, W(T) 612
Tree, weight of a tree 612
Tree, weights for an optimal tree 612
Tremblay, Jean-Paul 704 708
Trend 33
Trial 179
Triangle inequality 767
Triangular number 193 198 482 572
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 (the empty string)
(the empty string) 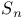 )
)  )
)