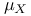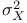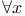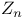|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grimaldi R.P., Rothman D.J. — Discrete and Combinatorial Mathematics: An Applied Introduction |
|
|
 |
| Предметный указатель |
Premise 53 67 70 107 109—111
Preorder (traversal) 592—597 616 619 620 623
Prescribed order 597 599 620 653 655
Preservation of Boolean algebra operations 739
Preservation of ring operations 698
Prim, Robert Clay 638 641 667 669
Primary key 272
Prime characteristics 812
Prime factorization 238 240
Prime integer (or number) 116 193 221 222 230 237 238
Prime order (for a group) 758
Prime polynomial 807
Primitive statement 48
Prim’s algorithm 641—643 653
Princeton University 706
Principia Mathematica 119 187
Principle of cross classification 411
Principle of duality for a Boolean algebra 735
Principle of duality for Boolean functions 713
Principle of duality for Boolean variables 713
Principle of duality for logic 59
Principle of duality for set theory 141
Principle of inclusion and exclusion 261 385 389—397 402 407 411 412 415 659
Principle of Mathematical Induction 194—196 198 200—206 213—216 218 244 315 317 390 425 441 448 468 469 599 see "The
Principle of Strong Mathematical Induction 206
Private-key cryptosystem 693 759 760
probability 3 42 123 150—189 247 262 402 408 409 411 428 430 468 506 759—765
probability distribution 176 177 179 180 428 430
Probability rules and laws 172
Probability, 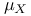 177 177
Probability, 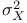 180 180
probability, additive rule 162 168 172
Probability, Axioms of probability 159 161
Probability, Bayes’Theorem 170 173 188
Probability, Bernoulli trial 161 178 179
Probability, Binomial probability distribution 179
Probability, Chebyshev’s Inequality 183 184 188
Probability, conditional probability 166—173
Probability, continuous sample space 164
Probability, discrete sample space 164 175
Probability, E(X) 111 182 183
Probability, elementary event 158
Probability, event 151 158 159
Probability, expectation 177
Probability, expected value 177 179 180
Probability, experiment 150—153
Probability, independent events 155 158 161 170
Probability, independent outcome 154 166 170 174
Probability, Kolmogorov, Andrei 159
Probability, law of total probability 169 170 173
Probability, mean 177 180 183
probability, multiplicative rule 168 172
Probability, mutually disjoint events 159
Probability, outcome 180 181 183
Probability, random variable 175—184
Probability, Rule of complement 159 172
Probability, sample space 150—155
Probability, standard deviation 180 182 183
Probability, variance 177 180
Problem of the 36 officers 819 831
Procedure for integer division 224
Procedure for the Euclidean algorithm 234
Proceedings of the Royal Geographical Society 565
Product of Boolean functions 712
Product of disjoint cycles 780 781 786
Product of matrices A-14
Product of maxterms 717 718
Product of sets 248
Program Evaluation and Review Technique (PERT) network 357 377
Program verification 203
Projection 270—272
Projective plane 827 828
proof 10 47 84 103 104 119 see "Mathematical "Mathematical
Proof by contradiction 76 77 80 84 99 114 115 127 137 237 273 291
Proper coloring of a graph 565—568 570
Proper divisors of 0 221
Proper divisors of zero 675 677 689 801
Proper prefix 312 315
Proper subgroup 748
Proper subset 124—126
Proper substring 313
Proper suffix 312
Properties of a Boolean Algebra 735 736
Properties of a group 747
Properties of exponents A-3
Properties of logarithms A-6
Properties of the integers 193—246
Properties of the integers, Division algorithm 223
Properties of the integers, Euclidean algorithm 232 233
Properties of the integers, Fundamental Theorem of Arithmetic 238
Properties of the integers, greatest common divisor 231 232
Properties of the integers, least common multiple 236
Properties of the integers, mathematical induction 193—208
Properties of the integers, primes 193 221 222 230 237 238
Properties of the integers, Well-Ordering Principle 194
Proposition 47 see
Propositional calculus 735
Pruefer code 586 587
Prune (a tree) 596
Pruned tree 611
Pseudocode procedure for binary search 502
Pseudocode procedure for bubblesort 450
Pseudocode procedure for Euclidean algorithm 234
Pseudocode procedure for exponentiation 297
Pseudocode procedure for Fibonacci numbers 477—479
Pseudocode procedure for gcd (recursive) 455
Pseudocode procedure for linear search 296
Pseudocode procedure for modular exponentiation 693
Pseudorandom numbers 689
Public-key cryptosystem 759 760
push 490—493
Puzo, Mario 186 692
q is necessary for p 48
Quadratic equation 794
Quadratic order 293
Quadratic time complexity 299
Quantified open statement 87
Quantifiers 91 98 103—105 119 125 146 195 291
Quantifiers,  88 88
Quantifiers, 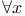 88 88
Quantifiers, bound variable 88
Quantifiers, connectives 88 89
Quantifiers, existential quantifier 87 88
Quantifiers, free variable 88
Quantifiers, implicit 89 90
Quantifiers, universal quantifier 87 88
Quantify 87
Quantum theory A-11
Quartic equation 794
Quasi-path 650
Quaternary alphabet 474
Quaternary relation 271
Quaternary sequence 247
QUEUE 598 599
Quick sort 609
Quine — McCluskey method 727 742
Quine, Willard van Orman 742 743
Quintic equation 794 830
Quintilianus, Marcus Fabius 705
Quotient 221 223 224
Quotient group 831
r(C, x) 404—406 408
Rabbits 505
Radicals 830
Ralston, Anthony 537 575 576
Ramsey theory 305
Ramsey, Frank Plumpton 305
Random variable 175—184 209 296 428 430
Random walk 506
Randomly generated numbers 689
| RANGE 175 253 392 393
Rank 559 819
Rate of a code 764 778 see
Ratio Test 429
Rational number exponent A-2
Rational numbers 133 194 A-30
Reachability 338
Reachable state 330
Reactor 486
Read, R.C. 566 571 574 576 796 797
Real numbers 133 139 194 A-27 A-28 A-30
Real-valued function 99
Rear (of a list) 598 599
Rearrangement 749
Reasoning system 86
Rebman, Kenneth R. 304 305
Received word 762 763 777 see
Record 694
Recurrence relations 447—510
Recurrence relations, analysis of algorithms 473
Recurrence relations, associated homogeneous relation 471—473 479 480
Recurrence relations, boundary conditions 448
Recurrence relations, characteristic equation 456
Recurrence relations, characteristic roots 456 468
Recurrence relations, constant coefficients 448
Recurrence relations, Fibonacci relation 457
Recurrence relations, first-order linear relation 448
Recurrence relations, general solution 456 468 471
Recurrence relations, geometric progression 447
Recurrence relations, homogeneous relation 448 450 456
Recurrence relations, initial condition 448 456
Recurrence relations, linear relation 449
Recurrence relations, linearly independent solutions 456 464
Recurrence relations, Maple code 477
Recurrence relations, method of generating functions 482—487
Recurrence relations, method of undetermined coefficients 471
Recurrence relations, nonhomogeneous relation 471 472
Recurrence relations, nonlinear relation 487—493
Recurrence relations, particular solution 471 475 479 482 487—493
Recurrence relations, second-order linear relations 456—468
Recurrence relations, system of recurrence relations 486 487
Recurrence relations, Table of particular solutions for the method of undetermined coefficients 479
Recurrence relations, variable coefficients 452
Recurrent event 506
Recursion 211
Recursive algorithm 453
Recursive algorithm for the Fibonacci numbers 477 478
Recursive construction 129 447 532 620
Recursive definition 210—218 251 255 282 312 317 447 594 A-1 A-26
Recursive function 259 453
recursive method 454
Recursive procedure 453 500 606 608
Recursive process 211—213 218 316
Recursively defined set 218 251 316
Reddy, M.R. 562 575
Redei, L. 559
Redfield, J. Howard 796 797
Reducible polynomial 807
Reductio ad absurdum 76 127
Redundant state 371 373
Reed, M.B. 574 576
Refinement (of a partition) 373
Reflections 750 781 782 788
Reflexive property (of a relation) 337—343 347 348 353 366—369 376 377 782 808
Regiments 819
Region 544
Regular graph 531
Reinelt, G. 562 576
Reingold, Edward Martin 506 508
Relation 211 247 250—256 271 282 303 337—378 513 737 780—783
Relation composition 344
Relation matrix 346—349
Relation, 1-equivalence 338
Relation, antisymmetric relation 340 341 347 348 353 357 358 376 377
Relation, associative law of composition 345
Relation, binary relation 250 337
Relation, composite relation 344
Relation, converse of a relation 282
Relation, definition of a relation 250
Relation, divides relation 339 737
Relation, equivalence relation 337 342 343 353 366—378
Relation, equivalent states 338 371
Relation, first level of reachability 338
Relation, irreflexive relation 344
Relation, k-equivalent states 338 371 372
Relation, modulo n relation 337
Relation, partial order 337 341—343
Relation, partial ordering relation 341 357
Relation, poset 357—364
Relation, powers of a relation 345
Relation, reachability 338
Relation, reflexive relation 337—343 366—369
Relation, relation composition 344
Relation, relation matrix 346—349
Relation, second level of reachability 338
Relation, subset relation 250 340 358 359
Relation, symmetric relation 339—343
Relation, transitive relation 339—343
Relation, zero-one matrix 344 347
Relational data base 271 272 305
Relative complement 138
Relative frequency 158 159
Relatively prime integers 232—234 236 240 394 470
Relatively prime polynomials 808
Relativity theory 707
Remainder 223—226 234 274 276 686 689 693 804 805 810
Remainder theorem 804 805
Rencontre 403
Renyi, A. 587
Repeated real roots 467
Repetition 7 26 27 41 125 149
replacement 92 96 106 114 115 124
Replication number 825
Representation Theorem for a finite Boolean algebra 738—741 743
Resek, Diane 119 120
Reset 321
Residue arithmetic 704
Resolution 86 119
Resolvent 86
Restriction of a function 257
Retransmission 765 769
Reversal function 318
Reversal of a string 317 319
Reverse order 620
Ribet, Kenneth 706
Right branch 488
Right child 590 594 610 611
Right children 594 595
Right coset 757
Right subtree 592 594—596
Right-cancellation property (in a group) 747
Rigid motions of a cube 791
Rigid motions of a regular hexagon 788
Rigid motions of a regular tetrahedron 792 793
Rigid motions of a square 750 780
Rigid motions of an equilateral triangle 749 750
Rinaldi, G. 562 576
Ring 673 674
Ring homomorphism 697—700 706
Ring isomorphism 697—704
Ring of matrices 674 705
Ring of polynomials 799 801
Ring theory 673—709
Ring theory, 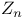 686 686
Ring theory, Boolean ring 709
Ring theory, cancellation law of multiplication 678 681
Ring theory, cancellation laws of addition 680
Ring theory, center of a ring 709
Ring theory, characteristic 812
Ring theory, commutative ring 675
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте