|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grimaldi R.P., Rothman D.J. — Discrete and Combinatorial Mathematics: An Applied Introduction |
|
|
 |
| Предметный указатель |
n-dimensional hypercube 532
n-fold product 248
n-tuple 248
Nand (connective) 66
NAND gate 727 728
Napier, John A-6
Natural logarithm 284 A-6
Natural numbers 133
Natural position 402
Nazi cipher 333
Neal, David 444
Nearest neighbor 771
Necessary and sufficient 48
Necessary condition 48
Negation 48
Negation (logic gate) 719
Negation of quantified statements 92 96 97
Negative 138
Negative integers 227
Nemhauser, G.L. 562 575 576
Nested multiplication method 301
network interface 12
network number 12
Network, dual 551—553
Network, electric power 666
Network, electrical 551 552 573 574 581 622
Network, gating 309 719—722 731
Network, logic 719 720
Network, multiple output 720 721
Network, parallel 64
Network, PERT 357 377
Network, Program Evaluation and Review Technique 357 377
Network, series 65
Network, switching 64—66
Network, transport 644—658
Neumann, Peter M. 796 797
Neutrons 486
New York Times 707
Newsom, Carroll V. 119 120 304 305
Newton, Sir Isaac 303
Next state 320
Next state function 320 682
Nicomachus of Gerasa 707
Nievergelt, Jurg 506 508
Nilsson, Nils J. 119 120
Nine-times repetition code 773 see
Niven, Ivan 243 244 444 445 708
No degree 800
Nobel prize 187
Node 349 514 see Vertices"
Noether, Emmy 706 707
Noise (in a binary symmetric channel) 761
Non-Euclidean geometry 820
Nonabelian group 749
Nonadjacent vertices 561
Noncommutative operation 590
Noncommutative ring 675 705
Nonempty universe 89
Nonequivalent configurations 783 784 790 791
Nonequivalent seating arrangements 784
Nonequivalent states 374
Nonexecutable specification statement 369
Nonhomogeneous recurrence relation 450 451 456 470—481
Nonlinear recurrence relations 449
Nonnegative integers 133
Nonplanar graph 540 541 543
Nontaking kings 510
Nontaking rooks 404 407
Nontrivial subgroup 748
Nonzero complex numbers 134
Nonzero division 221 356
Nonzero rational numbers 133
Nonzero real numbers 134
Nor (connective) 66
NOR gate 727 728
Normal subgroup 795 831
Not p 48
Not... and (connective) 66
Not... or (connective) 66
Null child 594 595
Null graph 523
Null set (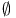 ) 127 ) 127
Number of divisions 458 459
Number of positive divisors 239
Number theory 29 188 222 242—244 303 304 394 411 412 432 442 673 705 706
Numerical analysis 304
O(g) (order of g) 290
O(g) on 5 498
Object program 253 302
octahedron 548
Octal system (base 8) 225
od(v) 535
od(z) 644
Odd integer 113 218
Odd-degree vertices 531
Officers 819
Ohm’s Law 573
Ohm’s Law for electrical flow 573
On the Theory of Groups, as Depending on the Symbolic Equation 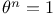 794 794
One element of a Boolean algebra 733
One factor 666
One-dimensional array 254
One-terminal-pair-graph 552
One-to-one correspondence 279 303 370 427 428 435 526 551 660 A-23—A-27
One-to-one function 255—257 279 280 409 410
One-unit delay machine 329
One’s complement 227—229
Onto function 260—265 287 288 392 411 439 682 699 739
Open contact 551 553
Open interval 99 100 134 164
Open statement 86 87 89—92 105 106 109 123 126 194 195
Open switch 64 551 553
Open trail 534
Open walk 515 516
Operand 136
Operation 136
Operations research 574 631 667
Optimal prefix code 613
Optimal spanning tree 638 639 642
Optimal tree 612 613 640—642
Optimization 41 324 562 581 631
Or (connective) 48
Or (exclusive) 48 56
OR gate 719—721
Order 6 14 15 30 125 130
Order at least 293
Order for a Boolean algebra 736
Order for functions 290 292 293
Order for the vertices of a tree 592 593
Order g (or, Order of g), O(g) 290—292
Order in a tree 588 589
Order of a finite field 812 813
Order of a group 746
Order of a group element 754
Order of a linear recurrence relation 456
Order of quantifiers 98
Order-preserving function 366 509
Ordered array 501—503
Ordered binary tree 488
Ordered pair 152 176 248 252 253 282 284
Ordered rooted tree 588
Ordered set 129 A-25
Ordered sum 205
Ordered tree 594
Ordered triples 827
Orderly permutation 455
Ordinary generating function 436 440 443 444 see
Ore, Oystein 561 668 669
Organic compounds 791—793
Origin (of an edge) 349 514
| Orlin, James B. 562 575 638 643 654 668
Orthogonal Latin squares 816—818 831
Out degree of a vertex 535 588 644
Outcome 150 151 154 155 158 175 177 178
Outgoing degree of a vertex 535
Output (for a finite state machine) 309 319
Output (from a gate) 720
Output (from an algorithm) 253 289
Output alphabet 320 321
Output function 320 682
Output string 321 322
Overcounting 19 20 411
Overflow error 229
O’Bryant, Kevin 623 624
p is sufficient for q 48
p logically implies q 69
p(m, n), the number of partitions of m into exactly n positive summands 444
p(n), the number of partitions of n 432 443
P(n, r) 7 15 41 436
Pair of orthogonal Latin squares 816—819 823
Pairs of rabbits 505
Pairwise disjoint subboards 405 408
Pairwise incidence matrix 826
Palindrome 13 174 197 319 425 426 431 432 460 461 469
Palmer, Edgar M. 574 576
Pan balance 602 603
Papadimitriou, Christos H. 333 334
Parallel algorithm 531
Parallel classes 822—824 828
Parallel computer 531
Parallel lines 822 827 828
Parallel network 64
Parent 588 593 597 613
Parenthesize an expression 38 39 490 494
Parity checks 778
Parity-check code 764 765 see
Parity-check equations 770 777 778 see
Parity-check matrix 772 774 776—779 see
Parker, Ernest Tilden 819 831
Partial breadth-first spanning tree 656
Partial fraction decomposition 426 483 485
Partial function 260
Partial order 337 341—343 356—364 376 377 476 533 737 738 see
Partial order for a Boolean algebra 736—738
Partial ordering relation 357 see "Poset"
Partial semipath 652
Partially ordered set 357 377 see
Particular solution 471 475 479 482
Partition 366—375 377 378
Partitions of integers 29 31 432—435 443 444
Pascal, Blaise 42 188 244
Pascal’s triangle 133 135 188
Patashnik, Oren 304 305 506 507
Path (in a graph) 351 516 517 556 582
Path (staircase) 9 36—38 130 132
Pattern 124
Pattern inventory 783 789—793
Pawlak, Zdzislaw 623
Peacock, George 186
Peano, Giuseppe 188 243 377
Peano’s postulates 243
Pegs 472 473
Peile, Robert E. 796
Peirce, Charles Sanders 119 377
Pendant vertex 533 549 583 584
Pennies 462 495
Pentium processor 5
Perfect integer 241
Perfect matching 666
Perfect square 90 239
Perfect, H. 668 669
Perl 4
Permutation 6—8 14 15 41 42 217 220 393 394 403 408 411 436 452 453 490—492 495 506 see
Permutation group 749 750 781 782 830 see
Permutation matrix 670
PERT network 357 377
Petersen graph 543 566 574
Petersen, Julius Peter Christian 574
Peterson, Gerald R. 742 743
Pi notation 239
Pigeonhole Principle 273—278 287 288 303—305 327 328 796
Plaintext 690—692 760
Planar graph 540—553 573
Planar-one-terminal-pair-graph 552
Planarity of graphs 352 615 see
Platonic solids 547 548 556
Pless, Vera 796 797
Points at infinity 828
Polaris submarine 357
Polish notation 591 592
Polya, George 623 625 745 796 797
Polya’s Method of Enumeration 623 779 789 891
Polya’s theory in graphical enumeration 574
Polyhedra 573
Polynomial equation 794
Polynomial evaluation algorithm 301
Polynomial in the indeterminate x 799
Polynomial order 293
Polynomial ring 801 830
Polynomial time complexity 293
pop 490—493
POSET 357—364
Poset, antichain 381
Poset, chain 381
Poset, glb (greatest lower bound) 363
Poset, greatest element 363
Poset, greatest lower bound (glb) 363
Poset, Hasse diagram 358—361
Poset, lattice 364
Poset, least element 363
Poset, least upper bound (lub) 363
Poset, length of a chain 381
Poset, lower bound 363
Poset, lub (least upper bound) 363
Poset, maximal chain 381
Poset, maximal element 362
Poset, minimal element 362
Poset, order-preserving function 366
Poset, topological sorting algorithm 360 361 363
Poset, total order 359—361
Poset, upper bound 363
Positive closure of a language 315
Positive integers 133 136 193
Positive rational numbers 133
Positive real numbers 134
Postorder (traversal) 592—595 623 628
Postulates 87 98 243
Power series 417 418 433 443 484
Power set 128 476 533
PowerBall 15
Powers of  310 310
Powers of a function 282
Powers of a group element 747
Powers of a language 315
Powers of a real number A-2
Powers of a relation 345
Powers of a ring element 802
Powers of an alphabet 310
Powers of strings 312
Pr(B|A) 167
Precedence graph 350
Precedes 347 348
Precise instructions 233
Pred (predecessor) function 307
Prefix 312 313 315 338
Prefix codes 609 611 613 614 624
Prefix notation 591
Pregel River 533
Preimage (of a set) 285 286
Preimage (of an element) 253
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



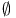 )
)