|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dunford N., Schwartz J.T., Bade W.G. — Linear Operators, Part II: Spectral Theory. Self Adjoint Operators in Hilbert Space (Pure and Applied Mathematics: A Series of Texts and Monographs) |
|
|
 |
| Предметный указатель |
Spectrum in a finite dimensional space VII.1.2 556
Spectrum in a general space VII.3.1 566
Spectrum of a B*-algebra IX.3.4 875
Spectrum of an element in a B-algebra IX.1.2 861
Spectrum of an element of a sub B-algebra IX.1 865
Spectrum of an unbounded operator 599
Spectrum of special bounded operators VII.5.2—VII.5.15 580—581
Spectrum of special unbounded operators VII.10.1—VII.10.3 604—605
Spectrum,  -simple function X.1 891 -simple function X.1 891
Spectrum, continuous VII.5.1 580 X.3.1
Spectrum, essential, of a closed operator XIII.6.1 1393
Spectrum, isolated point of VII.3.15 571
Spectrum, point VII.5.1 580 X.3.1
Spectrum, residual VII.5.1 580 X.3.1
Sphere in a metric space I.6.1 19
Sphere, closed II.4.1 70
Sphere, closed unit II.3.1 59
Sreider, Y. 392
Stability of a system of differential equations VII.2.23 564
Stasevskaya, V.V. 1588 1626
Steinhaus, H. 80—81 94 387—388
Stekloff, W. 1583
Stepanoff, W. 729
Stewart, F.M. 233
Stickelberger, L. 607
Stieltjes moment problem XII.2 1253
Stieltjes, T.J. 132 142 929 1250 1253 1269
Stokes, G.G. 383 1527
Stone and Banach see also "Banach — Stone theorem"
Stone space, definition 398
Stone theorems on representation of Boolean rings and algebras I.12.1 41 44
Stone — Cech compactification theorem IV.6.22 276 IX.2.16
Stone — Cech compactification theorem, remarks on 385
Stone — Weierstrass theorem IV.6.16 272
Stone — Weierstrass theorem, complex case IV.6.17 274
Stone — Weierstrass theorem, remarks on 383—385
Stone, M.H. 41 48 80 85 272 279 382 383—385 393 396 398 442 460 466 606 608 726 872 884 926 927 928 929 1243 1268 1269 1270 1272 1273 1274 1276 1277 1586 1588 1590 1591 1616 1619
Strictly convex B-space, definition VII.7 458
Strong operator topology, definition VI.1.2 475
Strong operator topology, properties VI.9.1—VI.9.5 511 VI.9.11—VI.9.12
Strong topology in a normed space II.3.1 59 419
Structure space of a B-algebra IX.2.7 869
Sturm — Liouville operator XIII.2 1291 XIII.9.F
Sturm, C. 1291 1462 1581 1582 1583
Subadditive function, definition 618
Subbase for a topology I.4.6 10
Subbase for a topology, criterion for I.4.8 11
Subspace of a linear space 36 see
Summability of Fourier series IV.14.34—IV.14.51 361—364
Summability of integrals IV.13.78—IV.13.101 351—356
Summability of series II.4.31—II.4.54 74—78
Summability, general principle of XIII.9.J2 1577
Summability, regular methods II.4.35 75
Summability, special types of, Abel II.4.42 76
Summability, special types of, Cesaro II.4.37 75 II.4.39 IV.14.44
Summability, special types of, Noerlund II.4.38 75
Summability, special types of, Poisson IV.14.47 363
Sunouchi, G. 233 234 391 543 552
Sup A 3
Support function, definition V.1.7 410
Supremum of a set of real numbers 3
Supremum, limit superior of a sequence of sets 126
Supremum, limit superior of a set of real numbers 4
Sylvester, J.J. 606—607
Symmetric difference 41 96
Symmetric operator, definition X.4.1 906 XII.1.7
Symmetric subspace, definition XII.4.4 1225
Szasz, O. 384
T(f,s) 668
T* 478 479 879 1188
Tagamlitzki, Y. 396 473
Takahashi, T. 388 400
Taldykin, A.T. 610
Tamarkin, J.D. 80 234—235 388 542 543 610 1118 1162 1269 1274 1276 1583
Tangent function, definition V.9.2 446
Tangent function, examples V.11.9—V.11.13 458—459
Tangent function, properties V.9.1 445 V.9.3 V.11.10—V.11.11
Tangent functionals, definition V.9.4 447
Tarski fixed-point theorem I.3.10 8
Tarski, A. 8
Tauber, A. 78 1007
Taylor expansion for analytic functions 228
Taylor, A.E. 92 233 399 540 543 552 554 606 608 612
Taylor, B. 1582
Tchebichef, P.L. 1512
Tchebicheff polynomial 369
Teichmueller, O. 48 927
Thorin, G.O. 541 1183
Tietze extension theorem I.5.3—I.5.4 15—17
Tietze, H. 15
Tingley, A.J. 406
Titchmarsh — Kodaira theorem XIII.5.18 1364
Titchmarsh, E.C. 48 612 1160 1364 1586 1587 1590 1591 1592 1614 1616 1618
Titov, N.S. 93
TM(S) or 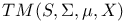 106 106
Toeplitz, O. 75 79 80 85 399 539 609 926 928 936 1269
Tomita, M. 473
Tonelli theorem III.11.14 194
Tonelli, L. 194
Topology of real numbers 11
Topology,  and and 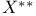 topologies in topologies in 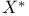 419 419
Topology, base and subbase for I.4.6 10
Topology, basic definitions I.4.1 10
Topology, bounded  topology V.5.3 427 topology V.5.3 427
Topology, functional or  topology V.3.2 419 topology V.3.2 419
Topology, functional or  topology, study of V.3 topology, study of V.3
Topology, linear spaces see "Operator topology"
Topology, metric or strong, in a B-space 419
Topology, metric or strong, study of I.6
Topology, metric, definition I.6.1 18
Topology, norm or strong, in a normed linear space II.3.1 59
Topology, product, definition I.8.1 32
Topology, study of I.4—I.8
Topology, topological group, definition II.1.1 49
Topology, topological space, definition I.4.1 10
Topology, topological space, study of I.4—I.8
Topology, weak* topology 462
Topology, weak, in a B-space 419
Tornheim, L. 884
Total boundedness in a metric space I.6.14 22
Total differential 92
Total disconnectedness 41
Total family of functions II.2.6 58
Total measurability, definition III.2.10 106 see
Total space of functionals, definition V.3.1 418
Total variation of a function III.5.15 140
Total variation of a function, of a set function III.1.4 97 see
Totally ordered set I.2.2 4
Tr A 1016
tr(S,T) 1026
Trace of a finite matrix VI.9.28 515 XI.6.8
Trace of a matrix, definition VI.9.28 515
Trace of two operators XI.6.17 1026
Transfinite closure of a manifold 462
Transformation see also "Operator"
Transformation, measure preserving 667
Transformation, metrically transitive 667
Translate of a function, definition 283
Translation by a vector 36
Translation number IV.7.2 282
Tseng, Y.Y. 94
Tsuji, M. 388 927
Tukey, J.W. 460—461
Tulajkov, A. 388
Tychonoff theorem on fixed points V.10.5 456 470
Tychonoff theorem on product spaces I.8.5 32
Tychonoff, A. 32 372 456 470
Udin, A.I. 396
Ulam, S. 91 1152
Ultrafilter, definition I.7.10 30
| Ultrafilter, properties I.7.11—I.7.12 30
Unbounded operators in Hilbert space Chap. XII
Unbounded operators, exercises on VII.10
Unbounded operators, remarks on 612
Unbounded operators, study of VII.9
Unconditional convergence of a series 92
Uniform boundedness principle for measures IV.9.8 309
Uniform boundedness principle in B-spaces II.3.20—II.3.21 66
Uniform boundedness principle in F-spaces II.1.11 52
Uniform boundedness principle, discussion of 80—82
Uniform continuity of an almost periodic function IV.7.4 283
Uniform continuity, criterion for I.6.18 24
Uniform continuity, definition I.6.16 23
Uniform continuity, extension of a function I.6.17 23
Uniform convergence as a criterion for limit interchange I.7.6 28
Uniform convergence,  -uniform convergence, criteria for III.6.2—III.6.3 145 III.6.12 -uniform convergence, criteria for III.6.2—III.6.3 145 III.6.12
Uniform convergence,  -uniform convergence, definition III.6.1 145 -uniform convergence, definition III.6.1 145
Uniform convergence, definition I.7.1 26
Uniform convergence, remarks concerning 382—383
Uniform convexity, definition II.4.27 74
Uniform convexity, properties II.4.28—II.4.29 74
Uniform convexity, remarks on 471—474
Uniform countable additivity see "Countably additive"
Uniform ergodic theory VIII.8
Uniform ergodic theory, remarks on 730
Uniform operator topology, definition VI.1.1 475
Uniform operator topology, properties VI.9.11—VI.9.12 512—513
Unit of a group 34
Unit sphere in a normed space, compactness and finite dimensionality of IV.3.5 245
Unit sphere in a normed space, definition II.3.1 59
Unit, adjunction of in a B-algebra IX.1 860
Unitary equivalence of operators X.5.12 919
Unitary operator X.4.1 906
Upper bound for an operator XII.5.1 1240
Urysohn theorems, for normal spaces I.5.2 15
Urysohn theorems, metrization I.6.19 24
Urysohn, P. 15 24
van Dantzig, D. 79 91
van Kampen, E.R. 1160
Variation of a  -continuous set function 131 -continuous set function 131
Variation of a countably additive set function III.4.7 128
Variation of a function III.5.15 140 see "Total
Variation of a regular set function III.5.12 137
Variation of a set function III.1.4—III.1.7 97—98
Variation, semi-variation of a vector-valued measure IV.10.3 320
Vaught, R.L. 884
Vector space, definition 36
Vector space, dimension of 36
Vector space, elementary properties I.11
Vector space, real or complex 49
Veress, P. 373 388 392
Vidav, I. 935
Vinkurov, V.G. 94
Vinogradov, A.A. 473
Visser, C. 610 728 933
Vitali theorems on convergence of integrals III.3.6 122 III.6.15 III.9.45 IV.10.9
Vitali theorems, covering theorem III.12.2 212
Vitali — Hahn — Saks Theorem III.7.2—III.7.4 158—160 IV.10.6
Vitali, G. 122 150 158 212 233—234 392
Volterra, V. 79 80 399
von Neumann, J. 80 85 88 235 372 380 386 389 393—394 438 461 538 611 612 659 727 728 884 886 926 927 928 933 934 1145 1152 1163 1240 1257 1263 1268 1269 1270 1272 1273 1274 1585 1588 1591
von Sz.-Nagy, B. 80 373 395 606 608 609 611 612 729 926 927 928 929 931 932 933 935 1259 1262 1263 1265 1270 1272 1273 1274
Vulich, B.Z. 93 396 540 543
Wallach, S. 1587 1592
Wallman, H. 467
Walsh, J.L. 1266 1616 1617
Walters, S.S. 399
Wassilkoff, D. 396
Watson, G.N. 1592
Weak Cauchy sequence, criteria for in special spaces IV.15
Weak Cauchy sequence, definition II.3.25 67
Weak completeness of reflexive spaces II.3.29 69
Weak completeness of special spaces IV.15
Weak completeness, definition II.3.25 67
Weak completeness, equivalence of weak and strong convergence in  IV.8.13—IV.8.14 295—296 IV.8.13—IV.8.14 295—296
Weak convergence in special spaces IV.15
Weak convergence, definition II.3.25 67
Weak convergence, properties II.3.26—II.3.27 68
Weak countable additivity and strong IV.10.1 318
Weak countable additivity, definition 318
Weak limit, definition II.3.25 67
Weak sequential compactness in reflexive spaces II.3.28 68
Weak sequential compactness in special spaces IV.15
Weak sequential compactness, definition II.3.25 67
Weak topology in a B-space 419
Weak topology, bounded  topology in topology in 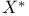 V.5.3 427 V.5.3 427
Weak topology, relations with reflexivity V.4
Weak topology, relations with separability and metrizability V.5
Weak topology, study of fundamental properties V.3
Weak topology, weak compactness V.6
Weak topology, weak operator topology, definition VI.1.3 476
Weak topology, weak operator topology, properties VI.9.1—VI.9.12 511—513
Weak topology, weak* topology 462
Weakly compact operator in  VI.8.1 498 VI.8.10—VI.8.14 VI.8.1 498 VI.8.10—VI.8.14
Weakly compact operator in 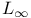 VI.9.57 519 VI.9.57 519
Weakly compact operator in C VI.7.1 490 VI.7.3—VI.7.6
Weakly compact operator, definition VI.4.1 482
Weakly compact operator, remarks on 539 541
Weakly compact operator, representation of 549
Weakly compact operator, spectral theory of, in certain spaces VII.4.6 580
Weakly compact operator, study of VI.4
Wecken, F.J. 927 928 929 933 1269
Wedderburn, J.H.M. 606
Wehausen, J.V. 83 91 381 462 471
Weierstrass, Approximation Theorem IV.6.16 272
Weierstrass, convergence theorem for analytic functions 228
Weierstrass, K. 228 232 272—273 383—384
Weierstrass, preparation theorem 232
Weil, A. 79 386 1145 1149 1152 1160 1274
Weinberger, H.F. 610
Weinstein, A. 928
Well-ordered set, definition I.2.8 7
Well-ordered set, well-ordering theorem I.2.9 7
Wentzel, G. 1614
Wermer, J. 385 930 931 935 1162
Westfall, J. 1583
Weyl — Kodaira theorems XIII.2.24 1301 XIII.5.13 XIII.5.14
Weyl, H. 372 610 612 725 940 1079 1145 1148 1149 1273 1301 1306 1351 1355 1584 1585 1586 1587 1588 1589 1590 1591
Weyr, E. 607
Whitney, H. 1162
Whittaker, E.T. 1592
Whyburn, G.T. 84
Whyburn, W.M. 1589
Widder, D.V. 383 728 1274
Wiegmann, N.A. 934
Wielandt, H. 934
Wiener closure theorem see "Closure theorem"
Wiener measure space 405
Wiener theorem on reciprocal of trigonometric series IX.4.10 881
Wiener — Levy theorem on analytic functions of trigonometric series IX.4.11 881
Wiener, N. 85 402 405 406 608 728—729 881 978 986 1003 1160 1264
Wilansky, A. 94
Wilder, R.L. 47
Wilkins, J.E., Jr. 936
Williamson, J.H. 609
Windau, W. 1585 1588
Wintner, A. 399 729 926 927 934 1552 1553 1555 1556 1557 1560 1585 1587 1590 1591 1597 1601 1602 1603 1605 1606 1607 1614 1616
Wolf, F. 612
Wolfson, K. 1587
Wright, F.B. 884
Yaglom, A.M. 407
Yamabe, H. 87
Yood, B. 474 610
Yosida see "Hille — Phillips — Yosida theorem"
Yosida, K. 233 234 373 396 466 539 541 624 715 726 727 728—730 927 929 1587 1628
Young, L.C. 542
Young, W.H. 529
Zaanen, A.C. 80 387 400 609 610 611 936 1277
Zalcwasser, Z. 462
Zermelo theorem on well-ordering I.2.9 7
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -simple function
-simple function 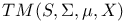
 and
and 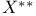 topologies in
topologies in 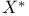
 topology
topology  -uniform convergence, criteria for
-uniform convergence, criteria for