|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dunford N., Schwartz J.T., Bade W.G. — Linear Operators, Part II: Spectral Theory. Self Adjoint Operators in Hilbert Space (Pure and Applied Mathematics: A Series of Texts and Monographs) |
|
|
 |
| Предметный указатель |
Base for a topology, definition I.4.6 10
Base for a topology, theorems concerning countable bases I.4.14 12 I.6.12 I.6.19
Basic separation theorem concerning convex sets V.1.12 412
Bellman, R. 1550
Bendixon, I. 1080
Bennett, A.A. 85
Berezanskii, Yu.M. 1587 1626
Berkowitz, J. 1543 1580 1591 1592 1594 1595 1599 1604
Bernoulli, D. 1581 1582
Bernstein theorem, concerning cardinal numbers I.14.2 46
Bernstein, F. 46
Berri, R. 395
Besicovitch, A.S. 386
Bessel equation XIII.8 1535
Bessel, F.W. 977 1348 1349 1535
Beurling, A. 361 930 978 1160 1161 1162
Bieberbach, L. 48
Bilateral Laplace and Laplace — Stieltjes transforms, definitions VIII.2.1 642
Bilinear functional II.4.4 70
Biorthogonal system in a B-space II.4.11 71
Birkhoff, G. 48 90 93 232 235 393—394 395 729
Birkhoff, G.D. 470 658—659 729 1497 1583 1586 1589 1592
Birnbaum, Z.W. 400
Blumenthal, L.M. 393
Boas, R.P., Jr. 94 473 1266
Bocher, M. 1583 1588 1589
Bochner moment problem XII.8.3 1254
Bochner, S. 232—233 235 283 315 386 390 395 540 543 552 883 1160 1254 1273 1274
Bodiou, G. 1264
Bogoliouboff, N. 730
Bohnenblust, H.F. 86 94 393 394 395—396 554
Bohr, H. 281 386—387 399 949 1149
Bohr, H., theorem concerning almost periodic functions XI.2.4 949
Boltzmann, L. 657
Bonnesen, T. 471
Bonsall, F.F. 88
Boolean algebra see also "Boolean ring"
Boolean algebra, definition 43
Boolean algebra, properties 44
Boolean algebra, representation of 44
Boolean ring, definition 40
Boolean ring, representation of I.12.1 41
Borel field of sets, definition III.5.10 137
Borel function X.1 891
Borel measurable function X.1 891
Borel measure (or Borel — Lebesgue measure), construction of 139 III.13.8
Borel — Stieltjes measure 142
Borel, E. 132 139 142 1588
Borg, G. 1561 1622
Borsuk, K. 91
Botts, T. 387 460
Bound in a partially ordered set I.2.3 4
Bound in the (extended) real number system 3
Bound, of an operator II.3.5 60
Boundary condition, adjoint XII.4.27 1237
Boundary condition, definition XII.4.25 1235 see boundary
Boundary condition, linearly independent XII.4.25 1235
Boundary condition, symmetric XII.4.25 1236
Boundary of a set I.4.9 11
Boundary values for an operator XII.4.20 1234
Boundary values, complete set of XII.4.22 1235 see
Bounded 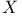 topology, continuous linear functionals V.5.6 428 topology, continuous linear functionals V.5.6 428
Bounded 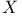 topology, system of neighborhoods for V.5.4 427 topology, system of neighborhoods for V.5.4 427
Bounded function space, additional properties IV.15
Bounded function space, definition IV.2.13 240
Bounded function space, remarks concerning 373
Bounded function space, study of IV.5
Bounded operator, definition II.3.5 60
Bounded set in a linear topological space II.1.7 51
Bounded set in a linear topological space, criterion for boundedness in a B-space II.3.3 59
Bounded set in a linear topological space, remarks on 80
Bounded sets in linear spaces V.7.5 436 V.7.7 V.7.8
Bounded strong operator topology, definition and properties VI.9.9 512
Bounded variation of a function, additional properties IV.15 378
Bounded variation of a function, criterion to be IV.13.73 350
Bounded variation of a function, definition III.5.15 140
Bounded variation of a function, generating Borel — Stieltjes measure 142
Bounded variation of a function, integral with respect to IV.13.63 349
Bounded variation of a function, integration by parts III.6.22 154
Bounded variation of a function, remarks on 392—393
Bounded variation of a function, right- and left-hand limits of III.5.16 140 III.6.21
Bounded variation of a function, set function, criteria for III.4.4—III.4.5 127—128 see
Bounded variation of a function, set function, definition III.1.4 97
Bounded variation of a function, study of IV.12
Bounded weak operator topology, definition and properties VI.9.7—VI.9.10 512
Bounded, essentially (or 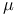 -essentially), definition III.1.11 101 -essentially), definition III.1.11 101
Bounded, totally bounded set, definition I.6.14 22
Boundedness of a continuous function on a compact set I.5.10 18
Boundedness of a finite countably additive set function III.4.4—III.4.7 127—128
Boundedness of an almost periodic function IV.7.3 283
Boundedness, principle of uniform boundedness in B-spaces II.3.20—II.3.21 66 80—82
Boundedness, principle of uniform boundedness in F-spaces II.1.11 52
Bounding point of a set, criteria for V.1.8 411 V.2.1
Bounding point of a set, definition V.1.6 410
Bourbaki, N. 47 80 82 84 232 382 463 465 471
Bourgin, D.G. 383 462
Brace, J.W. 466
Bram, J. 932 933
Brauer, A. 1078
Brauer, R. 1149
Bray, H.E. 391
Brelot, M. 1268
Brillouin, L. 1592 1614
Brodskii, M.S. 471 1164
Brouwer fixed point theorem, proof of 467
Brouwer fixed point theorem, statement 453
Browder, F.E. 1269 1634 1635 1708 1746
Brown, A. 934 935
BS 240
Buchheim, A. 607
Buniakowsky, V. 372
Burkhardt, H. 1589
bv 239
BV(I) 241
C 239
C(S) 240
Cafiero, F. 389 392
Calderon — Zygmund convolution kernel of XI.7.4 1053
Calderon — Zygmund convolution product of XI.7.6 1054
Calderon — Zygmund inequality XI.7.11 1063 XI.7.16
Calderon, A.P. 541 730 1063 1072 1077 1164 1165
Calkin, J.W. 553 1270 1273 1586 1589
Cameron, R.H. 406 407
Camp, B.H. 390
Canonical factorization of operators XII.7
Cantor diagonal process 23
Cantor perfect set V.2.13—V.2.14 436
Caratheodory theorem, concerning outer measures III.5.4 134
Caratheodory, C. 48 134 232 729 1043
Cardinal numbers, Bernstein theorem I.14.2 46
Cardinal numbers, comparability theorem I.3.5 8
Carleman, T. 536 927 1162 1163 1268 1269 1277
Carleman’s inequality XI.6.27 1038
Cartan, E. 607 1148
Cartan, H. 30 1152 1160 1274
Cartesian product of sets, definition I.3.11 9
Cartesian product of sets, properties I.3.12—I.3.14 9
Cartesian product of topological spaces I.8 31
Category theorem of Baire I.6.9 20
Cauchy integral formula 227
Cauchy integral formula for functions of an operator, in a finite dimensional space VII.1.10 560
Cauchy integral formula for functions of an operator, in general space VII.3.9 568
Cauchy integral formula for unbounded closed operators VII.9.4 601
Cauchy integral formula, remarks on 607—609 612
Cauchy integral theorem 225
Cauchy problem 613—614 639—641
Cauchy sequence in a metric space I.6.5 19—20
Cauchy sequence, generalized 28
Cauchy sequence, weak, criterion for in various spaces IV.15
Cauchy sequence, weak, in a B-space II.3.25 67—68
| Cauchy, A. 372 382—383
Cayley, A. 1270 1271
Cech compactification theorem IV.6.22 276
Cech compactification theorem of a completely regular space 279
Cech, E. 279 385 872
Cesaro summability of Fourier series IV.14.44 363
Cesaro summability of series II.4.37 75
Cesaro, E. 75 352 363
Chang, S.H. 610 1163
Change of variables for functions III.13.4—III.13.5 222—223
Change of variables for measures III.10.8 182
Character group, definition XI.3.13 968
Character, definition XI.1.5 944
Characteristic function 3
Characteristic polynomial, definition VII.2.1 561 XI.6.9
Characteristic polynomial, properties VII.2.1—VII.2.4 561—562 VII.5.17 VII.10.8
Characteristic value 606
Characterizations of 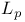 394—396 394—396
Characterizations of Hilbert space 393—394
Characterizations of the space of continuous functions 394—397
Charzynski, Z. 91
Chevalley, C. 79
Chiang, T.P. 928
Christian, R.R. 233 382 543 927
Clarkson, J.A. 235 384 393 396 397 473
Clifford, A.H. 92
Closed curve, positive orientation of 225
Closed graph theorem II.2.4 57
Closed graph theorem, remarks on 83—85
Closed linear manifold spanned by a set II.1.4 50
Closed operator, definition II.2.3 57
Closed orthonormal system, definition IV.14.1 357
Closed orthonormal system, study of IV.14
Closed set, definition I.4.3 10
Closed set, properties I.4.4—I.4.5 10
Closed sphere II.4.1 70
Closed unit sphere II.3.1 59
Closure of a set, criterion to be in I.7.2 27
Closure of a set, definition I.4.9 11
Closure of a set, properties of the closure operation I.4.10—I.4.11 11—12
Closure of a symmetric operator, definition XII.4.7 1226
Closure theorems XI.4 978—1001
Closure theorems, Wiener, 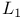 XI.4.7 986 XI.4.7 986
Closure theorems, Wiener, as a Tauberian theorem XI.5.C 1003
Closure theorems, Wiener, generalization of XI.4.21 996
Cluster point of a set I.7.8 29
co(A) 414
Coddington, E.A. 1433 1434 1498 1503 1587 1590 1591 1592
Cohen, I.S. 400
Cohen, L.W. 543 729
Collatz, L. 610 928
Collins, H.S. 466
Commutator of two operators, definition X.9 934
Compact operator in 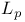 VI.9.51—VI.9.57 517—519 VI.9.51—VI.9.57 517—519
Compact operator in C VI.9.45 516
Compact operator, criteria for and properties of VI.9.30—VI.9.35 515
Compact operator, definition VI.5.1 485
Compact operator, elementary properties VI.5
Compact operator, ideals of 552—553
Compact operator, remarks concerning 539 609—611
Compact operator, representation of 547—551
Compact operator, representation of, into C(S) VI.7.1 490
Compact operator, representation of, on 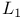 VI.8.11 507 VI.8.11 507
Compact operator, representation of, on C(S) VI.7.7 496
Compact operator, spectral theory of VII.4 VII.5.35 VII.8.2
Compact space, conditional compactness I.5.5 17
Compact space, criteria for compactness I.5.6 17 I.7.9 I.7.12
Compact space, definition I.5.5 17
Compact space, metric spaces I.6.13 21—22 I.6.18—I.6.19
Compact space, properties I.5.6—I.5.10 17—18
Compact space, sequential compactness, definition I.6.10 21
Compact space, weak sequential compactness, conditions for in special B-spaces IV.15
Compact space, weak sequential compactness, definition II.3.25 67
Compact space, weak sequential compactness, in reflexive spaces II.3.28 68
Complement of a set 2
Complement, and projections 553—554
Complement, orthocomplement IV.4.3 249
Complement, orthogonal II.4.17 72
Complemented lattice 43
Complete and  -complete lattice 43 -complete lattice 43
Complete metric space, compact I.6.15 22
Complete metric space, definition I.6.5 19
Complete metric space, properties I.6.7 20 I.6.9
Complete normed linear space see "B-space"
Complete orthonormal set in Hilbert space IV.4.8 250
Complete partially ordered space, definition I.3.9 8
Completely regular space, compactification of IV.6.22 276 IX.2.16
Completely regular space, definition IV.6.21 276 IX.2.15
Completion of a normed linear space 89
Complex numbers, extended 3
Complex vector space 38 49
Conditional compactness, definition I.5.5 17 see
Cone, definition V.9.9 451
Confluent hypergeometric function XIII.8 1526
Conjugate space, definition II.3.7 61
Conjugate space, representation for special spaces IV.15
Conjugations in groups 35
Conjugations in Hilbert space XII.4.17 1231
Connected set in n-space 230
Connected space I.4.12 12
Continuity of functionals and topology V.3.8—V.3.9 420—421 V.3.11—V.3.12
Continuity of functionals and topology in bounded 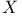 -topology V.5.6 428 -topology V.5.6 428
Continuity of functionals and topology, criteria for existence of continuous linear functionals V.7.3 436
Continuity of functionals and topology, non-existence in 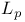 , 0<p<1 V.7.37 438 , 0<p<1 V.7.37 438
Continuous (or 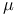 -continuous set functions), criterion for III.14.13 131 -continuous set functions), criterion for III.14.13 131
Continuous (or 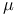 -continuous set functions), definition III.4.12 131 -continuous set functions), definition III.4.12 131
Continuous (or 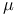 -continuous set functions), derivative of III.12.6 214 -continuous set functions), derivative of III.12.6 214
Continuous (or 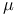 -continuous set functions), relation with absolutely continuous functions 338 -continuous set functions), relation with absolutely continuous functions 338
Continuous (or 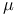 -continuous set functions), relation with integrable functions III.10 -continuous set functions), relation with integrable functions III.10
Continuous functions see also "Absolutely continuous functions"
Continuous functions as a B-space, additional properties IV.15
Continuous functions as a B-space, definition IV.2.14 240
Continuous functions as a B-space, remarks concerning 373—386
Continuous functions as a B-space, study of IV.6
Continuous functions on a compact space I.5.8 18 I.5.10
Continuous functions, characterizations of C-space 396—397
Continuous functions, criteria and properties of I.4.16—I.4.18 13—14 I.6.8 I.7.4
Continuous functions, criteria for the limit to be continuous I.7.7 29 IV.6.11
Continuous functions, definition I.4.15 13
Continuous functions, density in TM and 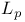 III.9.14 170 IV.8.19 III.9.14 170 IV.8.19
Continuous functions, existence of non-differentiable continuous functions I.9.6 33
Continuous functions, existence on a normal space I.5.2 15
Continuous functions, extension of I.5.3—I.5.4 15—17 I.6.17
Continuous functions, representation as a C-space, almost periodic functions IV.7.6 285
Continuous functions, representation as a C-space, bounded functions IV.6.18—IV.6.22 274—277
Continuous functions, special C-spaces 397—398
Continuous functions, uniform continuity I.6.16—I.6.18 23—24
Continuous functions, uniform continuity, of almost periodic functions IV.7.4 283
Convergence of filters I.7.10 30
Convergence of functions IV.15
Convergence of functions in 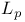 , criteria for III.3.6—III.3.7 122—124 III.6.15 III.9.5 IV.8.12—IV.8.14 388 , criteria for III.3.6—III.3.7 122—124 III.6.15 III.9.5 IV.8.12—IV.8.14 388
Convergence of functions in measure (or in 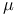 -measure), counter examples concerning III.9.4 169 III.9.33 -measure), counter examples concerning III.9.4 169 III.9.33
Convergence of functions in measure (or in 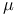 -measure), definition III.2.6 104 -measure), definition III.2.6 104
Convergence of functions in measure (or in 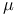 -measure), properties III.2.7—III.2.8 104—105 III.6.2—III.6.3 III.6.13 -measure), properties III.2.7—III.2.8 104—105 III.6.2—III.6.3 III.6.13
Convergence of functions, 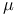 -uniform, criteria for III.6.2—III.6.3 145 III.6.12 -uniform, criteria for III.6.2—III.6.3 145 III.6.12
Convergence of functions, 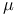 -uniform, definition III.6.1 145 -uniform, definition III.6.1 145
Convergence of functions, almost everywhere, criteria for III.6.12—III.6.13 149—150
Convergence of functions, almost everywhere, definition III.1.11 100
Convergence of functions, almost everywhere, properties III.6.14—III.6.17 150—151
Convergence of functions, quasi-uniform, definition IV.6.10 268
Convergence of functions, quasi-uniform, properties IV.6.11—IV.6.12 268—269 IV.6.30—IV.6.31
Convergence of functions, uniform, definition I.7.1 26
Convergence of functions, uniform, properties I.7.6—I.7.7 28—29
Convergence of sequences in a metric space I.6.5 19
Convergence of sequences in special spaces IV.15
Convergence of sequences, generalized I.7.1—I.7.7 26—29
Convergence of sequences, weak convergence in a B-space II.3.25 67
Convergence of series in a B-space, absolute 93
Convergence of series in a B-space, unconditional 92
Convergence of sets, definition 126—127
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



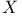 topology, continuous linear functionals
topology, continuous linear functionals 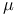 -essentially), definition
-essentially), definition 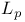
 -complete lattice
-complete lattice