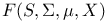|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dunford N., Schwartz J.T., Bade W.G. — Linear Operators, Part II: Spectral Theory. Self Adjoint Operators in Hilbert Space (Pure and Applied Mathematics: A Series of Texts and Monographs) |
|
|
 |
| Предметный указатель |
Convergence of sets, measurable sets in 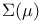 III.7.1 158 III.7.1 158
Convergence of sets, properties III.9.48 174
Convergence of sets, set functions III.7.2—III.7.4 158—160 IV.8.8 IV.9.4—IV.9.5 IV.9.15 IV.10.6 IV.15
Convergence of sets, set functions, remarks on 389—392
Convergence theorems IV.15
Convergence theorems for functions of an operator, by inverting sequences VIII.2.13 650
Convergence theorems for functions of an operator, examples of VII.8
Convergence theorems for functions of an operator, in finite dimensional spaces VII.1.9 559 see
Convergence theorems for functions of an operator, in general spaces VII.3.13 571 VII.3.23 VII.5.32
Convergence theorems for functions of an operator, study of VII.7
Convergence theorems for kernels III.12.10—III.12.12 219—222
Convergence theorems for linear operators in F- and B-spaces II.1.17—II.1.18 54—55 II.3.6 80—82
Convergence theorems, Alexandroff theorem on convergence of measures IV.9.15 316
Convergence theorems, Arzela theorem on continuous limits IV.6.11 268
Convergence theorems, Banach theorem for operators into space of measurable functions IV.11.2—IV.11.3 332—333
Convergence theorems, Egoroff theorem on a.e. and 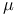 -uniform convergence III.6.12 149 -uniform convergence III.6.12 149
Convergence theorems, Fatou theorem on limits of integrals III.6.19 152 III.9.35
Convergence theorems, Lebesgue dominated convergence theorem III.3.7 124 III.6.16 IV.10.10
Convergence theorems, Moore theorem on interchange of limits I.7.6 28
Convergence theorems, Vitali theorem for integrals III.3.6 122 III.6.15 III.9.45 IV.10.9
Convergence theorems, Vitali — Hahn — Saks theorem for measures III.7.2—III.7.4 158—160
Convergence theorems, Weierstrass theorem on analytic functions 228
Convex combination V.2.2 414 see "Convex "Convex
Convex function, definition VI.10.1 520
Convex function, study of VI.10
Convex hull V.2.2 414
Convex set II.4.1 70
Convex set, definition V.1.1 410
Convex set, study of V.1—V.2
Convex space, locally V.2.9 417 471
Convex space, strictly V.11.7 458
Convex space, uniformly, defined II.4.27 74
Convex space, uniformly, remarks on 471—474
Convexity theorem of M. Riesz VI.10.11 525
Convexity theorem of M. Riesz, applications of VI.11
Convolution of functions as an operator in 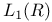 XI.3.3 954 XI.3.3 954
Convolution of functions, definition VIII.1.23 633
Convolution of functions, inequalities concerning VI.11.6—VI.11.12 528—529
Convolution of functions, properties VIII.1.24—VIII.1.25 634—635 XI.3.1
Convolution of measures VIII.2.3 643
Cooke, R.G. 80 926 927
Cooper, J.L.B. 927 932 1258 1273
Correspondence see "Function"
Coset, definition 35
Countably additive set function see also "Set function"
Countably additive set function, countable additivity of the integral III.6.18 152 IV.10.8
Countably additive set function, definition III.4.1 126
Countably additive set function, extension of III.5
Countably additive set function, integration with respect to III.6 IV.10
Countably additive set function, properties IV.9 IV.15
Countably additive set function, spaces of III.7 IV.2.16—IV.2.17
Countably additive set function, study of III.4
Countably additive set function, uniform countable additivity III.7.2 158 III.7.4 IV.8.8—IV.8.9 IV.9.1
Countably additive set function, weak countable additivity, definition 318
Countably additive set function, weak countable additivity, equivalence with strong IV.10 318
Covering of a topological space in the sense of Vitali, definition III.12.2 212
Covering of a topological space in the sense of Vitali, Vitali covering theorem III.12.3 212
Covering of a topological space, definition I.5.5 17
Covering of a topological space, Heine — Borel covering theorem 17
Covering of a topological space, Lindeloef covering theorem 12
Cronin, J. 92
Cross product see "Product"
CS 240
Curve see "Jordan curve" "Rectifiable
D(I) 1645
da Silvas Dias, C.L. 399
Daniell, P.J. 381—382
Darboux, G. 1588
Davis, H.T. 80
Day, M.M. 82 233 393—394 398 463 729
De Morgan, rules of 2
Decomposition of measures and spaces, Hahn decomposition III.4.10 129
Decomposition of measures and spaces, Jordan decomposition, for finitely additive set functions III.1.7 98
Decomposition of measures and spaces, Jordan decomposition, for measures III.4.7 128 III.4.11
Decomposition of measures and spaces, Lebesgue decomposition III.4.14 132
Decomposition of measures and spaces, Saks decomposition IV.9.7 308
Decomposition of measures and spaces, Yosida — Hewitt decomposition 233
Deficiency indices and spaces, definition XII.4.9 1226
Delsarte, J. 1626
Dense convex sets V.7.27 437
Dense linear manifolds V.7.40—V.7.41 438—439
Dense set, definition I.6.11 21
Dense set, density of continuous functions in TM and 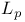 III.9.17 170 IV.8.19 III.9.17 170 IV.8.19
Dense set, density of simple functions in 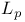 , ,  III.3.8 125 III.3.8 125
Dense set, nowhere dense set I.6.11 21
Density of the natural embedding of a B-space 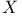 into into 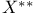 in the in the 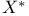 topology V.4.5—V.4.6 424—425 topology V.4.5—V.4.6 424—425
Derivative of a set function III.12.4 212
Derivative of functions III.12.7—III.12.8 216—217 III.13.3 III.13.6
Derivative of Radon — Nikodym 182
Derivative, chain rule for III.13.1 222
Derivative, existence of III.12.6 214
Derivative, properties IV.15
Derivative, references for differentiation 235
Derivative, space of differentiable functions IV.2.23 242
Determinant, definition 44—45
Determinant, elementary properties of I.13
Diagonal process 23
Diameter of a set, definition I.6.1 19
Diametral point V.11.14 459
Dieudonne, J.A. 82 84 94 235 387—388 389 391 395 399—400 402 460 462—463 465 466 539 541
Differentiability of the norm, remarks on 471—473 474
Differential calculus see also "Derivative"
Differential calculus in a B-space 92—93
Differential calculus, Frechet differential 92
Differential equations, solutions of systems of 561 VII.2.19 VII.5.16 VII.5.27
Differential equations, stability of VII.2.20—VII.2.29 564—565
Differential operator in 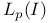 XIII.9.E 1549 XIII.9.E 1549
Differential operator, boundary condition at an end point for XIII.2.29 1304
Differential operator, boundary condition for XIII.2.17 1297
Differential operator, boundary form for XIII.2.1 1287
Differential operator, boundary matrix for XIII.2.1 1287
Differential operator, boundary value for XIII.2.17 1297
Differential operator, bounded below XIII.7.20 1451 XIII.9.C
Differential operator, branching point of XIII.7.62 1490
Differential operator, characteristic equation of, at infinity XIII.8 1527
Differential operator, complete set of boundary values for XIII.2.17 1297
Differential operator, determining set for XIII.5.22 1374
Differential operator, essential spectrum of XIII.10.E 1607
Differential operator, finite below 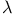 XIII.7.25 1455 XIII.7.25 1455
Differential operator, first characteristics of XIII.8 1527
Differential operator, formal XIII.1.1 1280
Differential operator, formal adjoint of XIII.2.1 1287
Differential operator, formally positive XIII.7.6 1439
Differential operator, formally self adjoint XIII.2.1 1287
Differential operator, Green’s formula for XIII.2.4 1288
Differential operator, indicial equation of XIII.8 1504
Differential operator, irregular formal XIII.1 1280
Differential operator, mixed boundary condition XIII.2.29 1304
Differential operator, nonselfadjoint XIII.9.13 1540
Differential operator, real boundary value for XIII.2.29 1304
Differential operator, regular formal XIII.1 1280
Differential operator, regular, irregular, singular points for XIII.8 1504
Differential operator, separated boundary conditions XIII.2.29 1304
Differential operator, singular boundary value of second order for XIII.10.D 1604
Differential operator, Stokes lines of XIII.8 1527
Differential operator, Sturm — Liouville XIII.2 1291 XIII.9.F
Differentiation theorems VIII.9.13—VIII.9.14 719—720 see
Dimension of a Hilbert space, as a criterion for Isometric isomorphism IV.4.16 254
Dimension of a Hilbert space, definition IV.4.15 254
Dimension of a Hilbert space, invariance of IV.4.14 253
Dimension of a linear space, definition 36
Dimension of a linear space, invariance of I.14.2 46
Dimension of a linear space, of a B-space 91—92
Dines, L.L. 466
Dini, U. 360 383 1583
Dirac, P.A.M. 402 1585 1648 1680
Direct product of B-spaces 89—90
Direct sum of B-spaces 89—90
Direct sum of Hilbert spaces IV.4.17 256
Direct sum of linear manifolds in a linear space 37
| Direct sum of linear spaces 37
Directed set, definition I.7.1 26
Disconnected, extremally 398
Disconnected, totally 41 see
Disjoint family of sets, definition 2
Distinguish between points, definition IV.6.15 272
Distributions XIV.3
Distributions, carrier or support of XIV.3.11 1650
Distributions, definition XIV.3.2 1645
Ditkin, V.A. 1161
Divisor of zero IX.1.2—IX.1.7 861
Dixmier, J. 94 398 538 886 935
Dixon, A.C. 1583
Doeblin, W. 730
Domain in complex variables 224
Domain of a function 2
Domain, k-parameter discrete case VIII.6.9 679
Domain, one-parameter continuous case VIII.7.7 693
Domain, one-parameter discrete case VIII.6.8 678
Domain, remarks on 729
Dominated Convergence Theorem III.3.7 124 III.6.16 IV.10.10
Dominated ergodic theorem, k-parameter continuous case in 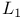 , ,  VIII.7.10 694 VIII.7.10 694
Doob, J.L. 729—730 927 929
Dorodnicyn, A.A. 1587
Double norm, definition XI.6.1 1010
Dowker, Y.N. 723—724 729
Dual group, definition XI.3.13 968
Dual space (or conjugate space), definition II.3.7 61
Dubrovskii, V.M. 389
Duffin, R.J. 1265
Dugundji, J. 470
Dunford, N. 82 84 93 232 235 384 387 389 392 462 540—541 543 554 606 609 612 724 727 729—730 927
Dunham, j.l. 1592
Dvoretsky, A. 93
D’Alembert, J. 1582
Eachus, J.J. 1265
Eberlein — Smulian theorem on weak compactness V.6.1 430
Eberlein — Smulian theorem on weak compactness, remarks on 466
Eberlein, W.F. 88 386 430 463 466 729 927 1273
Edwards, R.E. 381 884
Egoroff theorem on almost everywhere and 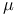 -uniform convergence III.6.12 149 -uniform convergence III.6.12 149
Egoroff, D.T. 149
Eidelheit, M. 91 460
Eigenvalue, definition VII.1.2 556 VII.11 X.3.1
Eigenvector, definition VII.1.2 556 X.3.1
Eilenberg, S. 385 397
Elconin, V. 92
Ellis, D. 394
Ellis, H.W. 400
Embedding, natural, of a B-space into its second conjugate II.3.18 66
End point of an interval III.5.15 140
End point of an interval, fixed XIII.1 1279
End point of an interval, free XIII.1 1279
Entire function, definition 231
Entire function, Liouville’s theorem on 231
Equicontinuity and compactness IV.5.6 260 IV.6.7—IV.6.9
Equicontinuity, definition IV.6.6 266
Equicontinuity, principle of II.1.11 52
Equicontinuity, quasi-equicontinuity, and compactness IV.6.14 269 IV.6.29
Equicontinuity, quasi-equicontinuity, definition IV.6.13 269 IV.6.28
Equicontinuous family of linear transformations, definition V.10.7 456
Equicontinuous family of linear transformations, fixed point of V.10.8 457
Equivalence of normed linear spaces, definition II.3.17 65
Equivalence, *-equivalence of B*-algebras IX.3.4 875
Erdoes, P. 384 407
Ergodic theorems VII.7 VII.8.8—VII.8.10 VIII.4—VIII.8 see "Maximal "Mean "Pointwise "Uniform
Ergodic theorems, remarks on 728—730
Esclangon, E. 1591
Essential least upper bound, definition III.1.11 100—101
Essential singularity, definition 229
Essential spectrum of a closed operator XIII.6.1 1393
Essential supremum, definition III.1.11 100—101
Essentially bounded, definition III.1.11 100—101
Essentially bounded, E- X.2 899
Essentially separably valued, definition III.1.11 100—101
Esser, M. 927
Euclidean space, definition IV.2.1 238
Euclidean space, further properties IV.15 374
Euclidean space, study of IV.3
Euler — Gauss, hypergeometric equation of XIII.8 1509
Euler, L. 1509 1510 1582
Extended real and complex numbers, definitions 3
Extended real and complex numbers, topology of 11
Extension of a function by continuity I.6.17 23
Extension of a function, definition 3
Extension of a function, Tietze’s theorem I.5.3—I.5.4 15—17
Extension of measures to arbitrary sets III.1.9—III.1.10 99—100
Extension of measures to arbitrary sets, Lebesgue III.5.17—III.5.18 142—143
Extension of measures to arbitrary sets, to a  -field III.5 -field III.5
Extensions of linear operators VI.2.5 478 554
Extremal point and subset, definitions V.8.1 439
Extremal point and subset, examples and properties V.11.1—V.11.6 457—458
Extremal point and subset, remarks on 466 473
Extremal point and subset, study of V.8
Extremally disconnected 398
Ezrohi, I.A. 543
F(S) or 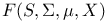 103 103
f(T) 557 568 601 1196
F*g 633 951
F-space basic properties II.1—II.2
F-space basic properties, definition II.1.10 51
F-space basic properties, examples of IV.2.27—IV.2.28 243
Factor group, definition 35
Factor sequence 366
Factor space in F- and B- spaces, definition II.4.13 71
Factor space in F- and B- spaces, properties II.4.13—II.4.20 71—72
Factor space in F- and B- spaces, remarks on 88
Factor space in vector spaces 38
Fagan, R.E. 406
Fage, M.K. 1587 1589
Fan, K. 395 397 610
Fantappie, L. 399 607
Farnell, A.B. 1163
Fatou theorem on limits and integrals III.6.19 152 III.9.35
Fatou, P. 152
Fell, J.M.G. 927
Feller, W. 727 1589 1628
Fenchel, W. 471
Feynman, R.P. 406
Fichtenholz, G. 83 233 373 386 388 543
Ficken, F.A. 393 394
Field in algebraic sense 36
Field of subsets of a set,  -field III.4.2 126 III.5.6 -field III.4.2 126 III.5.6
Field of subsets of a set, Borel field III.5.10 137
Field of subsets of a set, definition III.1.3 96
Field of subsets of a set, determined by a collection of sets III.5.6 135
Field of subsets of a set, Lebesgue extension of a  -field III.5.18 143 -field III.5.18 143
Field of subsets of a set, restriction of a set function to 166
Filter, definition and properties I.7.10—I.7.12 30—31
Finite dimensional function on a group, definition XI.1.3 940
Finite dimensional spaces, additional properties IV.15 374
Finite dimensional spaces, definitions IV.2.1—IV.2.3 238—239
Finite dimensional spaces, study of IV.3
Finite intersection property, as criterion for compactness I.5.6 17
Finite intersection property, definition I.5.5 17
Finite measure (space),  -finite measure III.5.7 136 see "Measure -finite measure III.5.7 136 see "Measure
Finite measure (space), criterion for and properties III.4.4—III.4.9 127—129
Finite measure (space), definition III.4.3 126
Finite measure (space), Saks decomposition of IV.9.7 308
Finitely additive set function see also "Set function"
Finitely additive set function, definition III.1.2 96
Finitely additive set function, study of III.1—III.3
Fischer, C.A. 380 539 543
Fischer, E. 373
Fixed point property, definition V.10.1 453
Fixed point property, exercises V.11.16—V.11.23 459—460
Fixed point property, remarks on 467—470 474
Fixed point property, theorems V.10
Fleischer, I. 88 400
Foias, C. 1267 1268
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -uniform convergence
-uniform convergence 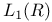
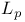

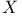 into
into 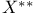 in the
in the 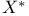 topology
topology 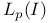
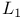 ,
, 
 -field
-field