|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dunford N., Schwartz J.T., Bade W.G. — Linear Operators, Part II: Spectral Theory. Self Adjoint Operators in Hilbert Space (Pure and Applied Mathematics: A Series of Texts and Monographs) |
|
|
 |
| Предметный указатель |
Jackson, D. 1589
Jacobi, C.G.J. 1275 1512
Jacobson, N. 48 935
James, R.C. 88 93 94 393—394 472—473
Jamison, S.L. 612
Jerison, M. 397 473
Jessen see "Fubini — Jessen theorems"
Jessen, B. 207 209 235 530
Jordan canonical form for a matrix VII.2.17 563
Jordan curve 225
Jordan decomposition of a measure III.4.7 128 III.4.11
Jordan decomposition of an additive real set function III.1.8 98
Jordan, C. 98 392
Jordan, P. 393—394
Jost, R. 1568 1626
Julia, G. 934
Kac, M. 406 407
Kaczmarz, S. 94
Kadison, R.V. 385 395 397
Kahane, J.P. 1161
Kakutani see "Markov — Kakutani theorem"
Kakutani, S. 86 90 235 380 384 386 393—394 395 396 456—457 460 462 463 471 473 539 541 554 715 728—730 1152
Kamke, E. 47
Kantorovitch, L.V. 233 373 386 388 395 540 543
Kaplansky theorem on 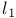 as a B-algebra IX.4.20 882 as a B-algebra IX.4.20 882
Kaplansky, I. 384—385 396 882 884 886 934 935 1161
Karaseva, T.M. 1587
Karlin, S. 93 94
Kato, T. 612 935
Katznelson, Y. 1161
Kay, I. 1622 1626
Kaz, I. 1590
Keldys, M.V. 611 1163
Kelley, J.L. 47—48 382 385 397 398 466 554 884 927 929
Kellogg, O.D. 470
Kemble, E.C. 1592
Kernel of a homomorphism 39 IV.13C IV.14
Kernel, convergence of III.12.10—III.12.12 219—222 IV.13C IV.14
Kerner, M. 92
Khintchine, A. 729
Kinoshita, A. 471
Klee, V.L. 87 90 460—461 466
Kleinecke, D.C. 553 610 612
Kneser, A. 1463 1583 1590 1592
Knopp, K. 48 536
Kober, H.A. 554
Kodaira theorem XIII.2.26 1302
Kodaira, K. 927 1152 1301 1302 1351 1355 1364 1586 1587 1589 1590
Koethe, G. 84 399 465
Kolmogoroff, A. 91 385 388
Komatuzaki 554
Koopman, B.O. 728 927 929
Koosis, P. 1161
Kostyucenko, A. 94 1587
Kozlov, V. 94
Krackovskii, S.N. 473 611
Kramer, H.P. 612
Kramer, V.A. 612
Kramers, H.A. 1592 1614
Krasnosel'skii, M.A. 400 611 1270 1273 1587 1591
Krein — Milman theorem on extremal points V.8.4 440
Krein — Smulian theorem on  closed convex sets in closed convex sets in 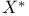 V.5.7 429 V.5.7 429
Krein — Smulian theorem on convex closure of a weakly compact set V.6.4 434
Krein, M. 94 387 395 396 397 429 434 440 461 463 465—466 611 612
Krein, M.G. 1160 1163 1270 1273 1587 1590 1591 1622 1626
Krein, S. 395 396 397
Kryloff, N. 730
Kuerschak, J. 79
Kuller, R.G. 395
Kunisawa, K. 391
Kuratowski, C. 83
Lacunary series, definition IV.14.63 366
Lagrange, J.L. 372 1582 1588
Laguerre, E.N. 607
Lalesco, T. 1081 1162
Lamson, K.W. 85
Landau, E. 80 1591
Langer, R.E. 1592
Laplace and Laplace — Stieltjes transform VIII.2.1 642
LaSalle, J.P. 91 399
Latshaw, V.V. 1589
Lattice, definitions 43
Laurent expansion 229
Lax, P.D. 88 1635 1748
Leader, S. 233
Least upper bound in a partially ordered set I.2.3 4
Least upper bound in the real numbers 3
Least upper bound, essential III.1.11 100 899
Lebesgue — Stieltjes measure on an interval 143
Lebesgue, decomposition theorem III.4.14 132 233
Lebesgue, dominated convergence theorem III.3.7 124 III.6.16 IV.10.10
Lebesgue, extension theorem III.5.17—III.5.18 142—143
Lebesgue, H. 80 124 132 143 151 218 232 234 390
Lebesgue, measure, in n-dimensional space III.11.6 188
Lebesgue, measure, on an interval 143
Lebesgue, set III.12.9 218
Lebesgue, spaces see " -spaces" -spaces"
Lefschetz, S. 47 467
Legendre, A.M. 1512
Leja, F. 79
Lengyel, B.A. 927 928 929
Leray, J. 84 470 609
Levi, B. 373
Levinson, N. 1266 1433 1434 1498 1503 1587 1590 1591 1592 1622
Levitan, B.M. 1587 1588 1590 1616 1622 1623 1624 1625 1626 1628
Levy, P. 407 881
Lezanski, T. 610
Lidskii, V.B. 1587 1591
Lie, S. 79
Lifsic, I.M. 612
lim inf A 4
lim sup A 4
LIMIT see also "Convergence"
Limit, Banach II.4.22—II.4.23 73
Limit, inferior (or superior), of a sequence of sets III.4.3 126
Limit, inferior (or superior), of a set or sequence of real numbers 4
Limit, point of a set I.4.1 10
Limit, weak, definition II.3.25 67
Limit, weak, in special spaces IV.15
Limit, weak, properties II.3.26—II.3.27 68
Lindeloef theorem I.4.14 12
Lindeloef, E. 12 1043 1115
Lindgren, B.W. 406
Line integral, definition 225
Linear dimension 91
Linear functional 38 see
Linear manifold 36 see
Linear operator 36 see
Linear space I.11
Linear space, normed II.3.1 59 see
Linear space, topological II.1.1 49
Linear transformation 36 see
Linearly independent 36
Lions, J.L. 1724 1726
Liouville theorem 231
Liouville, J. 1291 1581 1582 1583
Littlewood, J.E. 78 531—532 541 718 1004 1006 1007 1076 1147 1177 1181 1183 1184 1591
Livingston, A.E. 399
Livsic, M.S. 611 1164 1587
Localization of series, definition 359
Locally compact space, definition I.5.5 17
Locally convex space, definition V.2.9 417
Locally convex space, local convexity, of  and weak topologies V.3.3 419 and weak topologies V.3.3 419
Locally convex space, local convexity, of 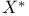 in the bounded in the bounded  topology V.5.5 428 topology V.5.5 428
Locally convex space, separation of convex sets in V.2.10—V.2.13 417—418
Loewig, H. 372 373
Loewner, K. 407
Loomis, L.H. 79 382 386 883 927 1145 1149 1152 1160 1161 1274
Lorch, E.R. 88 94 393—394 407 554 609 728 884 927
Lorentz, G.G. 84 400 543
| Lower bound for an operator XII.5.1 1240
lub A 3
Lumer, G. 931 933
M(S) or 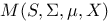 106 106
Maak, W. 386
MacDuffee, C.C. 606 607
Mackey, G.W. 393—394 554 1160 1161
MacLane, S. 48
Macphail, M.S. 93
Maddaus, I. 93 543 552
Maeda, F. 395 1274
Malliavin, P. 1161
Mandelbrojt, S. 1161
Manifold in a linear space 36 see
Manifold, closed linear, spanned by a set II.1.4 50
Manifold, orthogonal, in Hilbert space IV.4.3 249
Mapping see also "Function"
Mapping, interior principle II.2.1 55
Mapping, interior principle, remarks on 83—85
Marcenko, V.A. 1587 1590
Marcinkiewicz, J. 720 1166 1180 1182
Marinescu, G. 609
Markouchevitch, A. 94
Markov process, application of uniform ergodic theory to VIII.8
Markov process, definition 659
Markov — Kakutani theorem on fixed points of affine maps V.10.6 456
Markov, A. 380 456 471
Martin, R.S. 79 610 883
Martin, W.T. 406
Marumaya, G. 406
Masani, P.R. 233
Maslow, A. 233
Matrix 44
Matrix of a projection VI.9.27 514
Matrix, characteristic polynomial of VII.2.1—VII.2.4 561—562
Matrix, exercises on VII.2
Matrix, hermitian 561
Matrix, Jordan canonical form for VII.2.17 563
Matrix, normal VII.2.14 563
Matrix, study of VII.1
Matrix, trace of VI.9.28 515
Mautner, F.I. 1269 1634 1708
Maximal element in a partially ordered space I.2.4 4
Maximal element, Hausdorff maximality theorem I.2.6 6
Maximal element, relative to a normal operator X.5.6 913
Maximal ergodic lemma, discrete case VIII.6.7 676
Maximal ergodic lemma, k-parameter case VIII.7.11 697
Maximal ergodic lemma, one-parameter continuous case VIII.7.6 690
Maximal ergodic lemma, remarks on 729
Maximal ideal, definition and existence in a ring 39
Maximum modulus theorem 230—231
Maxwell, J.C. 1749
Mazur theorem on the convex hull of a compact set V.2.6 416
Mazur, S. 80 81—82 83 91—92 392 400 416 460 461—462 466 472 883
McShane, E.J. 84 232—233 382 387 927
Mean ergodic theorem 728—729
Mean ergodic theorem, continuous case in B-space VIII.7.1—VIII.7.3 687—689
Mean ergodic theorem, continuous case in B-space, in  VIII.7.4 689 VIII.7.4 689
Mean ergodic theorem, continuous case in B-space, in  VIII.7.10 694 VIII.7.10 694
Mean ergodic theorem, discrete case in B-space VIII.5.1—VIII.5.4 661—662
Mean ergodic theorem, discrete case in B-space, in  VIII.5.5 662 VIII.5.5 662
Mean ergodic theorem, discrete case in B-space, in  VIII.5.9 667 VIII.5.9 667
Mean Fubini — Jessen theorem III.11.24 207
Measurable function, conditions for (total) measurability III.2.21 116 III.6.9—III.6.11 III.6.14 III.9.9 III.9.11 III.9.18 III.9.24 III.9.37 III.9.44 III.13.11
Measurable function, definition III.2.10 106
Measurable function, extensions of the notion of measurability 118—119 322
Measurable function, properties III.2.11—III.2.12 106
Measurable function, space of totally,  -measurable function IV.2.12 240 891 -measurable function IV.2.12 240 891
Measurable function, space of totally, as a topological linear space III.9.7 169 III.9.28
Measurable function, space of totally, criterion for completeness III.6.5 146
Measurable function, space of totally, definition III.2.10 106 IV.2.27
Measurable function, space of totally, properties III.2.11—III.2.12 106
Measurable function, space of totally, remarks concerning 392
Measurable function, space of totally, study of TM IV.11 IV.15
Measurable set, definition III.4.3 126
Measure see also "Set function"
Measure of hypersurface of unit sphere in 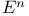 XI.7 1048—1049 XI.7 1048—1049
Measure space as a metric space III.7.1 158 III.9.6
Measure space,  -finite III.5.7 136 -finite III.5.7 136
Measure space, decomposition of see also "Decomposition"
Measure space, definition III.4.3 126
Measure space, finite III.4.3 126
Measure space, Lebesgue extension of III.5.18 143
Measure space, positive III.4.3 126
Measure space, product, of finite number of c-finite measure spaces 188
Measure space, product, of finite number of finite measure spaces III.11.3 186
Measure space, product, of infinite number of finite measure spaces III.11.21 205
Measure, -preserving transformation 667
Measure, Borel or Borel — Lebesgue 139
Measure, Borel — Stieltjes 142
Measure, Borel — Stieltjes, decomposition of see "Decomposition"
Measure, Borel — Stieltjes, determined by a function 142 144
Measure, Borel — Stieltjes, differentiation of III.12
Measure, change of III.10.8 182 X.1
Measure, definition III.4.3 126
Measure, Haar V.11.22—V.11.23 460
Measure, Hausdorff  - III.9.47 174 - III.9.47 174
Measure, invariant VI.9.38—VI.9.44 516
Measure, Lebesgue and Lebesgue — Stieltjes 143
Measure, Lebesgue extension of III.5.18 143
Measure, outer III.5.3 133
Measure, positive matrix XIII.5.12 1349
Measure, product III.11
Measure, Radon 142
Measure, regular vector-valued IV.13.75 350
Measure, restriction of 166
Measure, spaces of III.7 IV.2.15—IV.2.17 IV.9 IV.15 389—391
Measure, vector-valued, study of IV.10 391
Medvedev, Yu.T. 392
Mercer, T. 1088
Mertens, F. 77
Metric spaces, complete I.6.5 19
Metric spaces, definition I.6.1 18
Metric spaces, properties I.6
Metric(s) I.6.1 18
Metric(s) topology in normed linear space II.3.1 59 419
Metric(s), invariant, in a group 90—91
Metric(s), invariant, in a linear space II.1.10 51
Metrically transitive transformation 667
Metrizability see also "Metrization"
Metrizability and dimensionality V.7.9 436 V.7.34—V.7.35
Metrizability and separability V.5.1—V.5.2 426 V.6.3 V.7.15
Metrization of a measure space III.7.1 158
Metrization of a regular space I.6.19 24
Metrization of the set of all functions III.2.1 102
Michael, E. 462 538
Michael, E.A. 886 931
Michal, A.D. 79 92 610 883
Mihlin, C.G. 1181
Mikusinski, J.G. 395
Miller, D.S. 392 724 729
Milman see "Krein — Milman theorem"
Milman, D.P. 94 440 463 466 471 473 1587 1591
Milne, W.E. 1592 1614
Mimura, Y. 541 928
Minimax principle X.4 908 XIII.9.D
Minkowski inequality III.3.3 120
Minkowski inequality, conditions for equality III.9.43 173
Minkowski Inequality, generalizations of VI.11.13—VI.11.18 530—531
Minkowski, H. 120 372 471
Miranda, C. 88 470
Mirkil, H. 1161
Miyadera, I. 727
Mohr, E. 1590
Molcanov, A.M. 1563 1587 1591
Monna, A.F. 233 400
Montroll, E.W. 406
Moore theorem, concerning interchange of limits I.7.6 28
Moore, E.H. 28 80 608
Moore, R.L. 48
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



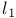 as a B-algebra
as a B-algebra  closed convex sets in
closed convex sets in 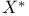
 -spaces"
-spaces" and weak topologies
and weak topologies 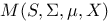

 -measurable function
-measurable function 
 -finite
-finite  -
-