|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dunford N., Schwartz J.T., Bade W.G. — Linear Operators, Part II: Spectral Theory. Self Adjoint Operators in Hilbert Space (Pure and Applied Mathematics: A Series of Texts and Monographs) |
|
|
 |
| Предметный указатель |
rba(S) 261
rca(S) 240
Real numbers, extended 3
Real numbers, topology of 11
Real part of a complex number 4
Real vector space 38 49
Rectifiable curve 225
Reflexivity, alternate proof V.7.11 436
Reflexivity, criterion for V.4.7 425
Reflexivity, definition II.3.22 66
Reflexivity, discussion 88
Reflexivity, examples of reflexive space IV.15
Reflexivity, properties II.3.23—II.3.24 67 II.3.28—II.3.29
Reflexivity, remarks on 463 473
Regular B-space see "Reflexivity"
Regular closure 462—463
Regular convexity 462—463
Regular element in a B-algebra IX.1.2 861
Regular element in a ring 40
Regular method of summability II.4.35 75
Regular point of a differential equation XIII.6 1432
Regular set function see also "Set function"
Regular set function, additional properties III.9.19—III.9.22 170
Regular set function, countable additivity and regularity III.5.13 138
Regular set function, definition III.5.11 137
Regular set function, extension of III.5.14 138
Regular set function, products of III.13.7 223
Regular set function, regularity of variations III.5.12 137
Regular set function, vector-valued measure IV.13.75 350
Regular singularity of a differential equation XIII.6 1432 XIII.6
Regular topological space, completely regular VI.6.21—VI.6.22 276
Regular topological space, definition I.5.1 15
Regular topological space, normality of, with countable base 24
Reid, W.T. 936
Relative topology, definition I.4.12 12
Rellich, F. 372 373 611—612 927 929 1263 1592 1593 1604
Representation as a space of continuous functions IV.6.18—IV.6.22 274—276 IV.7.6 394—397
Representation as a space of integrable functions 394—396
Representation for Boolean algebras 44
Representation for Boolean rings with unit I.12.1 41
Representation for conjugate spaces IV.15
Representation for unitary groups of operators XII.6.1 1243
Representation for vector-valued integrals III.11.17 198
Representation of a vector-valued function 196
Representation of finitely additive set functions IV.9.10—IV.9.11 312 IV.9.13
Representation of operators, in  VI.8 540—541 VI.8 540—541
Representation of operators, in C VI.7 539—540
Representation of operators, in other spaces 542—552
Resolution of the identity X.I 889
Resolution of the identity for a normal operator X.2.5 898
Resolution of the identity for an unbounded operator XII.2.4 1196
Resolution of the identity, formula for X.6.1 920 XII.2.10
Resolvent of an element in a B-algebra IX.1.2 861
Resolvent, definition VII.3.1 566
Resolvent, equation VII.3.6 566
Resolvent, set VII.3.1 566
Resolvent, set of an element in a B-algebra IX.1.2 861
Resolvent, study of VII.3
Rickart, C.E. 233 234 541 543 883 886
Riemann, B. 1508 1592
Riesz convexity theorem VI.10 VI.10.11
Riesz convexity theorem, applications and extensions VI.11
Riesz convexity theorem, inequality of XI.1.8 1059
Riesz convexity theorem, remarks on 541—542
Riesz, F. 79 80—81 85—86 88 265 372—373 380 387 388 392 395 538 539 606 608 609 659 728—729 926 927 928 929 933 935 1268 1269 1272 1273 1274
Riesz, M. 388 525 532 541 1059 1164
Rinehart, R.F. 607
Ring (algebraic), Boolean 40
Ring (algebraic), definition 35
Ring (algebraic), properties 40—44
Ring (algebraic), study of I.11—I.12
Riss, J. 1161
Ritz, W. 928
Roberts, B.D. 93
Rogers, C.A. 93
Rohlin, V.A. 929 1269
Rosenblatt, M. 406
Rosenbloom, P.C. 47 612
Rosenfeld, N.S. 1614 1615
Rosenthal, A. 232 234—235 390
Rosser, J.B. 47—48
Rota, extension theory of XIII.10.F 1612
Rota, G.C. 1612
Rotational invariance 402—403
Rotho, E.H. 92 470
Rubin, H. 393
Rudin, W. 385
Ruston, A.F. 473 610
Rutickii, Ya.B. 400
Rutman, M. 94 395 466
Rutovitz, D. 1616 1621
Ryll-Nardzewski, C. 683 724 729
S 243
Saks decomposition of a measure space IV.9.7 308
Saks, S. 80 82 158 232 233—235 308 380 390 392 462 720
Salem, R. 542
San Juan, R. 387
Sargent, W.L.C. 81 400
Scalar product in a Hilbert space IV.2.26 242
Scalars 36
Schaeffer, J.J. 931 932 933 934
Schaefke, F.W. 94 612
Schatten, R. 90 1163
Schauder, J. 83 84 93—94 456 470 485 539 609
Schmidt, E. 79 88 539 609 1087 1260 1269 1584 1590
Schoenberg, I.J. 380 393—394 728 1274
Schreiber, M. 932
Schreier, O. 79 462
Schroeder, J. 612
Schroedinger, E. 611 1585
Schur, I. 532
Schur, J. 77 388
Schwartz, H.M. 391
Schwartz, J.T. 375 387 389 392 540 543 612 1269 1588
Schwartz, L. 82 84 399 401 402 466 611 1161 1162 1645
Schwarz inequality IV.4.1 248
Schwarz, H.A. 248 372
Schwerdtfeger, H. 606
Sears, D.B. 1590 1591 1597 1604 1607 1616 1619
Sebastiao e Silva, J. 235 399
Segal, I.E. 384 727 928 929 1160 1161 1269
Seidel, P.L. 383
Seitz, F. 1592
Self adjoint operator X.4.1 906
Self adjoint subspace XII.4.14 1230
Semi-bounded operators, definition XII.5.1 1240
Semi-group of operators, definition VIII.1.1 614
Semi-group of operators, infinitesimal generator of VIII.1.6 619
Semi-group of operators, k-parameter VIII.7.8 693
Semi-group of operators, perturbation theory of 630—639
Semi-group of operators, strongly continuous 685
Semi-group of operators, strongly measurable 685
Semi-group of operators, study of VIII.1—VIII.3
Semi-simple B-algebra IX.2.5 869
Semi-variation of a vector-valued measure, definition IV.10.3 320
Semi-variation of a vector-valued measure, properties IV.10.4 320
Separability and compact sets V.7.15—V.7.16 437
Separability and compact sets, criterion for V.7.36 438
Separability and compact sets, of C V.7.17 437
Separability and embedding V.7.12 436 V.7.14
Separability and metrizability V.5.1—V.5.2 426
Separable linear manifolds II.1.5 50 see
Separable linear manifolds in  III.8.5 168 III.9.6 III.8.5 168 III.9.6
Separable linear manifolds in C IV.13.16 340
Separable sets I.6.11 21 see
Separably-valued III.1.11 100
Separation of convex sets in finite dimensional spaces V.7.24 437
Separation of convex sets in linear spaces V.1.12 412
Separation of convex sets in linear topological spaces V.2.7—V.2.13 417—418
Separation of convex sets, counter examples V.7.25—V.7.28 437
| SEQUENCE see also "Convergence"
Sequence of sets, non-increasing and limits of III.4.3 126
Sequence, Cauchy I.6.5 19
Sequence, Cauchy, generalized I.7.4 28
Sequence, Cauchy, weak II.3.25 67
Sequence, convergent I.6.5 19
Sequence, factor 366
Sequence, generalized I.7.1 26
Sequence, generalized, generated by an ultrafilter 280
Sequence, spaces of, definitions IV.2.4—IV.2.11 239—240 IV.2.28
Sequence, spaces of, properties IV.15
Sequential compactness, definition I.6.10 21
Sequential compactness, relations with other compactness in metric spaces I.6.13 21 I.6.15
Sequential compactness, weak, definition II.3.25 67
Sequential compactness, weak, in reflexive spaces II.3.28 68
Sequential compactness, weak, in special spaces IV.15
Series see also "Convergence"
Series, lacunary IV.14.63 366
Series, orthogonal IV.14
Series, summability of II.4.31—II.4.54 74—78
Set function,  -finite III.5.7 136 -finite III.5.7 136
Set function, additive III.1.2 96
Set function, bounded variation of III.1.4 97
Set function, continuity of III.4.12 131 III.10
Set function, convergence of III.7.2—III.7.4 158—160 IV.9 IV.15
Set function, countable additive III.4.1 126
Set function, countable additive, study of III.4
Set function, decomposition of III.1.8 98 III.4.7—III.4.14 233
Set function, definition III.1.1 95
Set function, differentiation of III.12
Set function, extensions of III.5
Set function, extensions of, non-uniqueness of III.9.12 169
Set function, extensions of, to a  -field III.5 -field III.5
Set function, extensions of, to arbitrary sets III.1.9—III.1.10 99—100
Set function, measure III.4.3 126
Set function, positive III.1.1 95
Set function, regular, definition III.5.11 137
Set function, regular, properties III.5.12—III.5.14 137—138 III.9.19—III.9.22 IV.13.75 IV.6.1—IV.6.3
Set function, relativization or restrictions of III.8
Set function, singular III.4.12 131
Set function, spaces of, as conjugate spaces IV.5.1 258 IV.5.3 IV.6.2—IV.6.3 IV.8.16
Set function, spaces of, definitions 160—162 IV.2.15—IV.2.17 IV.6.1
Set function, spaces of, remarks on 389—390
Set function, spaces of, study of III.7 IV.9—IV.10 IV.15
Set function, variation of III.1.4 97
Set(s) in 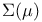 III.7.1 158 III.7.1 158
Set(s),  -set III.5.1 133 -set III.5.1 133
Set(s),  -field of III.4.2 126 -field of III.4.2 126
Set(s), Borel III.5.10 137
Set(s), convergence of 126—127 III.9.48
Set(s), field of III.1.3 96
Set(s), Lebesgue III.12.9 218
Set(s), open see "Open"
Shapiro, J.M. 406
Shiffman, M. 88
Shohat, J.A. 1274 1276
Sikorski, R. 610
Silberstein, J.P.O. 610
Silov, G. 384 385 883 884 1161
Silverman, L.L. 75
Simple function(s), definition III.2.9 105
Simple function(s), density in  , ,  of III.3.8 125 III.8.3 III.9.46 of III.3.8 125 III.8.3 III.9.46
Simple Jordan curve 225
Sin, D. 1588
Singer, I.M. 935
Singular element in a B-algebra IX.1.2 861
Singular element in a ring 40
Singular element in a ring, non-singular operator 45
Singular set function, definition III.4.12 131
Singular set function, derivatives of III.12.6 214
Singular set function, Lebesgue decomposition theorem III.4.14 132
Singularity of an analytic function 229
Sirohov, M.F. 395
Sirvint, G. 383 386 539—540 541 543
Skorohod, A. 94
Smiley, M.F. 394 395
Smith, K.T. 610 927 930 1120
Smithies, F. 543 610 1082 1083 1162
Smulian and Eberlein theorem on weak compactness V.6.1 430
Smulian and Krein see "Krein — Smulian theorem"
Smulian, criterion for  -compactness 464 -compactness 464
Smulian, criterion for weak compactness V.6.2 433
Smulian, V.L. 392 395 429 430 433 434 461 463—464 465—466 472—473 612
Snol, E. 1562 1563 1587 1591 1596 1600 1601 1610
Sobczyk, A. 86 393—394 553—554
Sobolev, S.L. 1680 1686
Solomyak, M.Z. 612
Soukhomlinoff, G.A. 86
sp(B) 50
Space Chap. IV
Space, B- and F-, elementary properties of Chap. II
Space, B- and F-, list of special spaces IV.2
Space, B- and F-, study of Chap. IV
Space, Banach see "B-space"
Space, Cech compactification of IV.6.27 279
Space, compact I.5.5 17
Space, complete I.6.5 19
Space, complete normed linear see "B-space"
Space, completely regular IV.6.21 276
Space, complex linear 38 49
Space, conjugate II.3.7 61
Space, connected I.4.12 12
Space, dimension of 36
Space, direct sum of 38
Space, extremally disconnected 398
Space, F-space II.1.10 51
Space, factor 38
Space, fixed point property of V.10.1 453
Space, Hausdorff I.5.1 15
Space, linear topological II.1.1 49
Space, locally compact I.5.5 17
Space, locally convex topological linear V.2.9 417
Space, measure III.4.3 126
Space, metric I.6.1 18
Space, normal I.5.1 15
Space, normal structure of V.11.14 459
Space, normed or normed linear II.3.1 59
Space, product I.8.1 32
Space, real linear 38 49
Space, reflexive II.3.22 66
Space, regular I.5.1 15
Space, separable I.6.11 21
Space, subspace 36
Space, subspace spanned 36
Space, topological I.4.1 10
Space, total, of functionals V.3.1 418
Space, totally disconnected 41
Span in a linear space 36 II.1.4
Sparre Andersen, E. 235
Spectral asymptotics XIII.10.G 1614
Spectral measure X.1 888
Spectral measure, countably additive X.1 889
Spectral measure, self adjoint X.1 892
Spectral multiplicity theory, definition X.5 913
Spectral radius of an element in a B-algebra IX.1.2 861
Spectral radius, definition VII.3.5 567
Spectral radius, properties VII.3.4 567 VII.5.11—VII.5.13
Spectral representation, definition X.5.1 909 XII.3.4 see
Spectral set of a bounded measurable function XI.4.10 988
Spectral set of von Neumann X.9 933
Spectral set, definition VII.3.17 572
Spectral set, properties VII.3.19—VII.3.21 574—575
Spectral synthesis, problem of XI.4 987
Spectral theorem for a B*-algebra X.2.1 895
Spectral theorem for a formally self adjoint differential operator XIII.5.1 1333
Spectral theorem for a normal operator X.2.4 897
Spectral theorem for a self adjoint differential operator with compact resolvent XIII.4.2 1331
Spectral theorem for an unbounded operator XII.2 1191
Spectral theory for compact operators VII.4
Spectral theory in a finite dimensional space VII.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте





 -finite
-finite 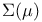
 -set
-set  of
of  -compactness
-compactness