|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dunford N., Schwartz J.T., Bade W.G. — Linear Operators, Part II: Spectral Theory. Self Adjoint Operators in Hilbert Space (Pure and Applied Mathematics: A Series of Texts and Monographs) |
|
|
 |
| Предметный указатель |
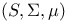 126 126
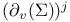 1699 1699
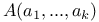 522 522
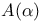 685 685
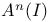 1280 1280
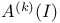 1652 1652
 619 619
 1662 1663 1662 1663
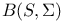 240 240
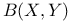 61 61
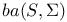 240 240
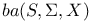 160 160
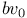 239 239
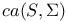 240 240
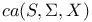 161 161
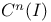 242 1638 242 1638
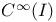 1638 1638
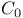 239 239
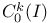 1638 1638
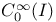 1638 1638
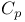 1089 1089
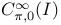 1660 1660
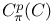 1660 1660
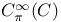 1660 1660
 1660 1660
 558 558
 573 573
 101 101
 238 238
 1684 1684
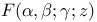 1509 1509
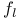 1668 1668
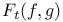 1287 1287
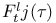 1287 1287
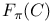 1660 1660
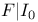 1649 1649
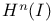 1287 1287
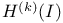 1652 1652
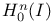 1291 1291
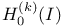 1652 1652
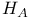 35 35
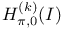 1662 1662
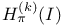 1662 1663 1662 1663
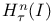 1287 1287
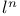 239 239
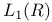 as a B-algebra XI.3.2 953 as a B-algebra XI.3.2 953
 239 239
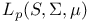 241 241
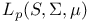 , ,  , characterizations of 394—396 , characterizations of 394—396
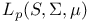 , ,  , completeness of III.6.6 146 III.9.10 , completeness of III.6.6 146 III.9.10
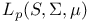 , ,  , criteria for convergence in III.3.6—III.3.7 122—124 III.6.15 IV.15 , criteria for convergence in III.3.6—III.3.7 122—124 III.6.15 IV.15
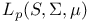 , ,  , definition III.3.4 121 , definition III.3.4 121
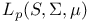 , ,  , remarks on 387—388 , remarks on 387—388
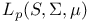 , ,  , separable manifolds in III.8.5 168 III.9.6 , separable manifolds in III.8.5 168 III.9.6
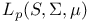 , ,  , study of III.3 III.6 IV.8 IV.15 , study of III.3 III.6 IV.8 IV.15
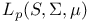 , 0<p<1, definition III.9.29 171 , 0<p<1, definition III.9.29 171
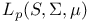 , 0<p<1, properties III.9.29—III.9.31 171 , 0<p<1, properties III.9.29—III.9.31 171
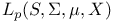 121 121
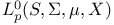 119 119
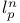 238 238
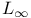 239 239
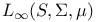 241 241
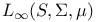 , definition IV.2.19 241 , definition IV.2.19 241
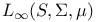 , study of IV.8 IV.15 , study of IV.8 IV.15
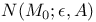 869 869
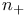 , , 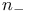 1227 1227
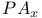 or or 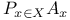 9 9
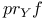 9 9
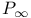 955 955
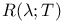 566 566
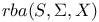 161 161
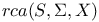 161 161
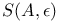 19 19
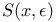 19 19
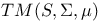 243 243
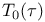 1291 1679 1291 1679
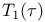 1291 1679 1291 1679
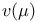 or or 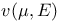 97 97
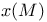 868 868
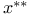 , , 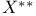 66 66
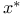 , , 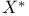 61 860 61 860
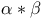 643 643
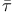 1639 1639
 1669 1669
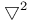 1631 1631
 96 96
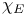 3 3
 1 1
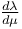 182 182
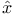 , , 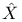 66 66
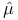 134 134
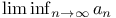 4 4
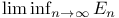 126 126
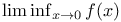 4 4
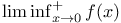 4 4
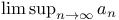 4 4
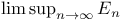 126 126
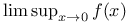 4 4
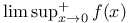 4 4
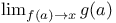 26 26
 126 126
 1050 1050
 630 630
 4 4
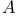 955 955
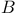 895 895
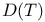 1185 1185
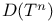 602 602
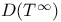 602 602
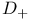 , , 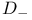 1226 1226
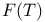 557 568 600 557 568 600
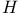 242 242
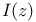 4 4
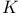 410 410
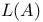 642 642
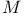 868 868
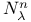 556 556
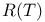 1185 1185
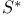 1230 1230
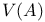 642 642
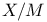 38 38
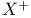 418 418
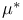 99 99
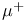 , , 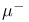 98 130 98 130
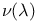 556 556
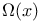 1052 1052
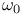 619 619
 249 249
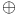 37 256 37 256
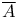 11 11
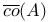 414 414
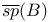 50 50
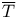 1226 1226
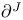 1636 1636
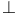 72 249 72 249
 1 1
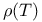 566 566
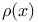 861 861
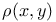 18 18
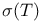 556 566 556 566
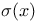 861 861
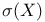 875 875
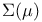 156 156
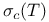 580 580
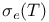 1393 1393
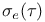 1393 1393
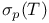 580 580
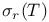 580 580
 446 963 446 963
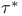 1639 1639
| 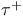 1639 1639
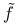 951 951
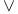 888 888
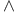 888 888
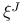 1635 1635
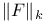 1663 1663
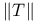 1010 1010
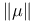 320 320
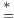 875 875
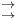 1645 1660 1645 1660
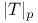 1089 1089
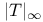 1089 1089
' 2
((S,T)) 1013
(a,b], etc. 4
(x,y) 242
(x,y)* 1224
a(a) 522
A(d) 242
A(n) 661
A(T,n) 661
a.e. see "Almost everywhere"
Abdelhay, J. 397
Abel summability of series II.4.42 76
Abel, N.H. 76 352 383
Abelian group 34
Absolute convergence, in a B-space 93
Absolutely continuous functions, definition IV.2.22 242
Absolutely continuous functions, set function see "Continuous set function" "Set
Absolutely continuous functions, space of, additional properties IV.15 378
Absolutely continuous functions, space of, definition IV.2.22 242
Absolutely continuous functions, space of, remarks concerning 392
Absolutely continuous functions, space of, study of IV.12.3 338
AC(I) 242
Accumulation, point of I.4.1 10
Adams, C.R. 393
Additive set function see "Set function"
Adjoint element in an algebra with involution 40 see
Adjoint of an operator between B-spaces VI.2
Adjoint of an operator in Hilbert space VI.2.9 479 VI.2.10
Adjoint of an operator, compact operator VI.5.2 485 VI.5.6 VII.4.2
Adjoint of an operator, continuity of operation VI.9.12 513
Adjoint of an operator, criterion for VI.9.13—VI.9.14 513
Adjoint of an operator, remarks on 538
Adjoint of an operator, resolvent of VII.3.7 568
Adjoint of an operator, spectra of VII.3.7 568 VII.5.9—VII.5.10 VII.5.23
Adjoint of an operator, weakly compact operator VI.4.7—VI.4.8 484—485
Adjoint space, definition II.3.7 61
Adjoint space, representation for special spaces IV.15
Affine mapping, definition 456
Affine mapping, fixed points of V.10.6 456
Agmon, S. 1161
Agnew, R.P. 87
Ahiezer, N.I. 926 927 929 1269 1270 1272 1273 1274 1276 1588 1589 1590 1592
Ahlfors, L.V. 48
Akilov, G.P. 554
Alaoglu, L. 235 424 462 463 729
Alexandroff theorem on C(S) convergence of bounded additive set functions IV.9.15 316
Alexandroff theorem on countable additivity of regular set functions on compact spaces III.5.13 138
Alexandroff, A.D. 138 233 316 380—381 390
Alexandroff, P. 47 467
Alexiewicz, A. 82 83 234 235 392 543
Algebra, algebraic preliminaries I.10—I.13
Algebra, B*-algebra IX.3
Algebra, B*-algebra, *-equivalences of B*-algebras IX.3.4 875
Algebra, B*-algebra, *-homomorphism in IX.3.4 875
Algebra, B*-algebra, *-isomorphism of IX.3.4 875
Algebra, B*-algebra, as an algebra of continuous functions IX.3.7 876
Algebra, B*-algebra, non-commutative IX.5 884—866
Algebra, B*-algebra, spectrum of IX.3.4 875
Algebra, B-algebra Chap. IX
Algebra, B-algebra, as an algebra of continuous functions IX.2.9 870
Algebra, B-algebra, as an operator algebra IX.1 860
Algebra, B-algebra, generating set for IX.2.10 870—871
Algebra, B-algebra, ideal in IX.1 865—866
Algebra, B-algebra, quotient IX.1 866
Algebra, B-algebra, radical of IX.2.5 869
Algebra, B-algebra, semi-simple IX.2.5 869
Algebra, B-algebra, structure space of 869
Algebra, boolean see also "Field of sets"
Algebra, Boolean, definition 43
Algebra, Boolean, representation of 44
Algebra, commutative IX.1.1 860 IX.2
Algebra, definition 40
Algebra, of sets see "Field of sets"
Algebra, quotient 40
Almost everywhere (or  -almost everywhere) definition for additive scalar set functions III.1.11 100 -almost everywhere) definition for additive scalar set functions III.1.11 100
Almost everywhere (or  -almost everywhere) definition for vector-valued set functions IV.10.6 322 -almost everywhere) definition for vector-valued set functions IV.10.6 322
Almost periodic functions, definition IV.2.25 242
Almost periodic functions, space of, additional properties IV.15 379
Almost periodic functions, space of, definition IV.2.25 242
Almost periodic functions, space of, remarks concerning 386—387
Almost periodic functions, space of, study of IV.7
Almost uniform (or  -uniform convergence) definition III.6.1 145 see -uniform convergence) definition III.6.1 145 see
Altman, M.S. 94 609 610
Ambrose, W. 1013 1160 1274
Analytic continuation 230
Analytic function (vector-valued) between complex vector spaces VI.10.5 522
Analytic function (vector-valued), definition 224
Analytic function (vector-valued), properties III.14
Analytic function (vector-valued), space of, definition IV.2.24 242
Analytic function (vector-valued), space of, properties IV.15
Annihilator of a set II.4.17 72
Anzai, H. 386
AP 242
Arens' lemma IX.3.5 875—876
Arens, R.F. 381 382 384 385 396—397 399 466 875 884 886
Arnous, E. 1274
Aronszajn, N. 87 91 234 394 610 928 930 1120
Artemenko, A. 387 392
Arzela theorem on continuity of limit function IV.6.11 268
Arzela theorem, remarks concerning 383
Arzela, C. 266 268 382 383
Ascoli — Arzela theorem on compactness of continuous functions IV.6.7 266
Ascoli — Arzela, remarks concerning 382
Ascoli, G. 266 382 460 466
Atkinson, F.V. 610 611 1615
Atom in a measure space IV.9.6 308
Audin, M. 611
Automorphisms in groups 35
B(s) 240
B*-algebras IX.3 874—879 see
B-algebra see "Algebra"
B-space (or Banach space), basic properties of Chap. II
B-space (or Banach space), definition II.3.2. 59
B-space (or Banach space), integration Chap. III
B-space (or Banach space), special B-spaces Chap. IV
B-space (or Banach space), special B-spaces properties IV.15
Babenko, K.I. 94 1183
Bade, W.G. 538 612 728 928 1269
Baire category theorem I.6.9 20
Baire, R. 20
Baker, H.F. 1588
Banach limits, existence and properties II.4.22—II.4.23 73
Banach theorem on convergence of measurable functions IV.11.2—IV.11.3 332—334
Banach — Stone theorem on equivalence of C-spaces V.8.8 442
Banach — Stone, remarks on 396—397 466
Banach, S. 59 62 73 80 81 82—84 85 86 89 91—93 94 234 332 380 385—386 392 442 462—463 465—466 472 538 539 609
Barankin, E.W. 1163
Bari, N.K. 94
Bartle, R.G. 85 92 233 383 386 389 392 539—540 543
Base (or basis) see also "Hamel base"
Base (or basis) in a B-space, criterion for compactness with IV.5.5 260
Base (or basis) in a B-space, definition II.4.7 71
Base (or basis) in a B-space, properties II.4.8—II.4.12 71
Base (or basis) in a B-space, remarks on 93—94
Base (or basis) in a linear space see "Hamel base"
Base (or basis), orthogonal and orthonormal bases in Hilbert space, definition IV.4.11 252
Base (or basis), orthogonal and orthonormal bases in Hilbert space, existence of IV.4.12 252
Base for a topology, criterion for I.4.7 11
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



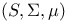
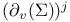
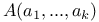
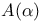
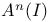
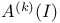
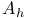
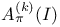
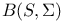
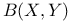
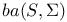
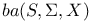
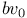
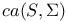
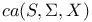
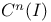
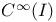
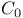
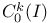
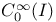
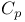
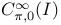
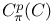


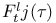
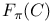
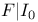
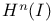
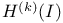
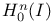
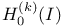
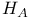
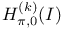
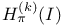
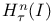
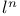
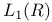 as a B-algebra
as a B-algebra 
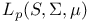
 , characterizations of
, characterizations of 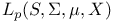
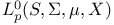
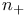 ,
, 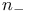
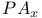 or
or 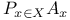
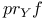
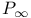
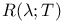
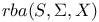
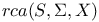
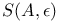
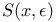
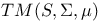
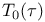
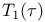
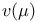 or
or 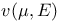
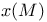
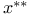 ,
, 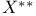
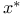 ,
, 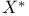
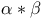
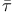

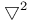

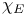

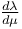
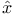 ,
, 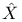
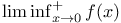
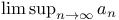
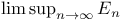
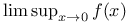
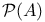
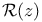
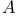
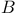
 ,
, 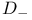
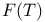
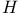
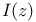
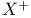
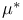
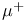 ,
, 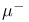
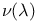
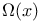
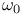

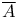
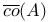
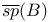
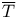
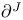
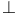

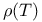
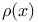
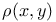
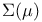
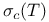
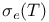
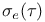
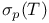
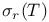

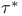
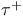
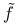
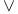
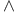
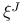
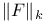
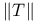
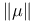
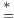
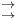
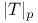
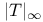
 -almost everywhere) definition for additive scalar set functions
-almost everywhere) definition for additive scalar set functions