|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dunford N., Schwartz J.T., Bade W.G. — Linear Operators, Part II: Spectral Theory. Self Adjoint Operators in Hilbert Space (Pure and Applied Mathematics: A Series of Texts and Monographs) |
|
|
 |
| Предметный указатель |
Folner, E. 399
Fort, M.K. 471
Fortet, R. 93 406 473
Fourier coefficients, definition IV.14.12 358
Fourier series, convergence of IV.14.27 360 IV.14.29—IV.14.33
Fourier series, definition IV.14.12 358
Fourier series, localization of IV.14.26 360
Fourier series, multiple series IV.14.68 367
Fourier series, multiple series, study of IV.14.69—IV.14.73 367—368
Fourier series, study of IV.14 IV.14.12—IV.14.20
Fourier sine and cosine theorems XIII.5 1388
Fourier, J.B.J. 1388
Frechet differential, definition 92
Frechet differential, theory for compact operators VII.4
Frechet, M. 79 233 373 380 382 387—388 392 730
Fredholm alternative 609—610
Fredholm, I. 79 609 1085
Freudenthal, H. 84 394 395 1273
Friedrichs, K.O. 401 405 407 612 927 1184 1240 1273 1501 1545 1546 1585 1586 1591 1592 1604 1635 1748 1749
Frink, O. 94
Frobenius, G. 607 1080 1147
Fubini theorem, for general finite measure spaces III.11.13 193
Fubini theorem, for positive  -finite measure spaces III.11.9 190 -finite measure spaces III.11.9 190
Fubini — Jessen theorems, mean III.11.24 207
Fubini — Jessen theorems, pointwise III.11.27 209
Fubini, G. 190 207 209
Fuchs, L. 1588
Fuglede, B. 934
Fukamiya, M. 466 729 884
Fullerton, R.E. 396 397 540 543 552
Function of an operator see "Calculus"
Function of bounded variation III.5.15 140
Function, absolutely continuous IV.2.22 242
Function, Additive set see "Set function"
Function, almost periodic IV.2.25 242 IV.7
Function, analytic III.14
Function, analytic, between complex vector spaces VI.10.5 522
Function, Borel — Stieltjes measure of III.5.17 142
Function, characteristic 3
Function, continuous I.4.15 13
Function, convex VI.10.1 520
Function, definition 3
Function, domain of 2—3
Function, entire 231
Function, essential bound or supremum of III.1.11 100
Function, extension of 3
Function, homeomorphism I.4.15 13
Function, homomorphism 35 39 40 44
Function, integrable III.2.17 112 IV.10.7
Function, inverse 3
Function, isometry II.3.17 65
Function, isomorphism 35 38 39
Function, linear functional 38
Function, linear operator 36
Function, measurable III.2.10 106 III.2.22 322
Function, metric I.6.1 18
Function, null III.2.3 103
Function, one-to-one 3
Function, operator 36
Function, orthonormal system of IV.14.1 357
Function, projection I.3.14 9 37 IV.4.8
Function, range of 3
Function, representation of vector valued III.11.15 194
Function, resolvent VII.3.1 566
Function, restriction of 3
Function, set III.1.1 95
Function, simple III.2.9 105 322
Function, subadditive 618
Function, support V.1.7 410
Function, tangent V.9.2 446
Function, total variation of III.5.15 140
Function, totally measurable III.2.10 106 see
Function, uniformly continuous I.6.16 23
Functional(s) in bounded  topology V.5.6 428 topology V.5.6 428
Functional(s) in weak and strong operator topologies VI.1.4 477
Functional(s), bilinear II.4.4 70
Functional(s), continuous II.3.7 61
Functional(s), continuous, existence of II.3.12—II.3.14 64—65
Functional(s), continuous, extension of II.3.10—II.3.11 62—63
Functional(s), continuous, for representation in special spaces IV.15
Functional(s), continuous, non-existence of 329—330 392
Functional(s), discontinuous, existence of I.3.7 8
Functional(s), linear 38
Functional(s), multiplicative IV.6.23 277
Functional(s), multiplicative, in the unit sphere of C* V.8.6 441
Functional(s), multiplicative, of 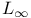 V.8.9 443 V.8.9 443
Functional(s), separating V.1.9 411
Functional(s), tangent V.9.4 447
Functional(s), total space of V.3.1 418
Functions of an element in a B*-algebra IX.3.12 878
Functions, special XIII.9.I 1569
Fundamental family of neighborhoods, definition I.4.6 10—11
Fundamental set in a linear topological space II.1.4 50
f{A} 644
Gagaev, B. 93
Gal, I.S. 80 82
Gale, D. 382
Gantmacher, V. 463 485 539
Garabedian, P.R. 88
Garding, L. 1269 1634 1708 1716
Gauss, C.F. 1509
Gavurin, M.K. 612
Gelbaum, B.R. 94
Gelfand — Neumark theorem IX.3.7 876
Gelfand, I.M. 79 94 232 235 347 384 385 396 407 539 540 543 608 609 876 883 884 1149 1160 1587 1616 1622 1623 1624 1625
Generalized sequence, definition and properties I.7.1—I.7.7 26—29
Generator, infinitesimal of a semigroup of operators VIII.1.6 619
Gibbs, J.W. 657
Gillespie, D.C. 462
Giorgi, G. 607
Glazman, I.M. 926 927 929 1269 1270 1272 1273 1274 1587 1588 1589 1590 1591 1592 1599
glb A 3
Glicksberg, I. 381
Glivenko, V. 391
Godement, R. 930 1160 1274
Goedel, K. 47—48
Gohberg, I.C. 610 611 1163
Gol'dman, M.A. 611
Goldstine, H.H. 81 424 463
Gomes, A.P. 399
Goodner, D.B. 398 554
Gowurin, M. 233 391 543 552
Graph of an operator II.2.3 57
Graph, closed graph theorem II.2.4 57
Graves, L.M. 48 85 92 232 235 383 391 467 611
Graves, R.E. 406
Graves, R.L. 610
Green's formula XIII.2.4 1288
Green, G. 1288
Grimshaw, M.E. 606
Grinblyum, M.M. 94
Grosberg, J. 395
Grosberg, Y. 392
Grothendieck, A. 90 383 389 398 399 466 540 543 552 553 610
Group, basic properties I.10
Group, definition 34
Group, metrizable 90
Group, representations 1145—1149
Group, topological II.1.1 49
Gurevic, L.A. 94
Haar measure on a compact group V.11.22—V.11.23 460 XI.1.1
Haar measure on a compact group in a locally compact group XI.3 950
Haar measure on a compact group in a locally compact group, properties of XI.11 1150—1155
Haar measure on a compact group, definition XI.1.2 940
Haar, A. 927 1147 1152 1583 1616 1617
Hadamard three circles theorem VI.11.48 538
Hadamard, J. 380 538 1018
Hadamard’s inequality XI.6.12 1018
Hahn decomposition theorem III.4.10 129
Hahn extension theorem III.5.8 136
| Hahn — Banach theorem II.3.10 62
Hahn — Banach theorem, discussion of 85—88
Hahn, H. 48 62 80 85 86 88 129 136 158 232 233 234—235 390 539 928 1269
Halberg, C.J.A., Jr. 1087
Halmos, P.R. 48 80 232 235 381 389 390 606 608 722 728 729 926 927 928 929 931 932 933 934 1152 1269
Halperin, I. 400 473 1586 1588 1591
Hamburger moment problem XII.8.1 1251
Hamburger, H.L. 606 611 1250 1251
Hamel base or basis for general vector spaces I.14.2 46
Hamel base or basis for real numbers I.3.7 8
Hamel base or basis, definition 36
Hankel transform XI.3.23 978 1535
Hankel, H. 1348 1349 1535
Hanson, E.H. 392
Harazov, D.F. 611
Hardy — Hilbert type inequalities VI.11.19—VI.11.29 531—534
Hardy, G.H. 78 364 531—533 538 541 718 1004 1006 1007 1076 1183 1184 1591
Hartman, P. 399 729 1551 1553 1555 1556 1558 1559 1560 1561 1562 1585 1587 1590 1591 1592 1596 1597 1598 1599 1600 1601 1602 1603 1605 1606 1607 1614 1615 1616 1626
Hatfield, C. 406
Hausdorff  -measure III.9.47 174 -measure III.9.47 174
Hausdorff maximality theorem I.2.6 6
Hausdorff space, criterion for I.7.3 27
Hausdorff space, definition I.5.1 15
Hausdorff, F. 6 47—48 79 89 174 380 529 539 1250
Heaviside, O. 1648
Heine — Borel theorem 17
Heinz, E. 612 933 935
Heinz, inequality of X.9 935
Heisenberg, W. 1264
Hellinger, E. 79 80 85 539 609 926 927 928 929 936 1269 1584
Helly, E. 81 86 380 391
Helson, H. 385 1160 1161
Hensel, K. 607
Herglotz, G. 365 1274
Hermitian matrix, definition 561
Hermitian operator, definition IV.13.72 350 X.4.1
Hewitt, E. 233 373 379 381—382 384—385 387
Heywood, P. 1615
Hilb, E. 608 1583 1584 1585 1589 1590
Hilbert cube see also "Hilbert space"
Hilbert cube as a fixed point in space V.10.2—V.10.3 453—454
Hilbert cube, definition and compactness IV.13.70 350 453
Hilbert proper value integral XI.7.8 1059
Hilbert Schmidt operators XI.6
Hilbert Schmidt operators, completeness of eigenfunctions XI.6.30 1041 XI.6.31
Hilbert Schmidt operators, definition XI.6.31 1042
Hilbert space, adjoint of an operator VI.2.9—VI.2.10 479—480
Hilbert space, finite dimensional IV.2.1 238 IV.3
Hilbert space, general, additional properties IV.15 379
Hilbert space, general, characterizations of 393—394
Hilbert space, general, definition IV.2.26 242 1773
Hilbert space, general, remarks on 372—373
Hilbert space, general, study of IV.4 1773—1784
Hilbert, D. 79—80 372 461 531—532 538—539 608 926 1083 1268 1584 1589 1590 1773
Hildebrandt, T.H. 81 85 92—93 233 373 380 388 391 392 609 1274
Hill, G.W. 1497
Hille — Yosida — Phillips theorem on the generation of semi-groups VIII.1.13 624
Hille, E. 80 92 543 606 608 610 612 624 726—727 729 883 1118 1162 1274 1628
Hirschman, I.I. 728 1183
Hobson, E.W. 383 1583
Hoelder inequality III.3.2 119
Hoelder inequality, conditions for equality in III.9.42 173
Hoelder inequality, generalizations of VI.11.1—VI.11.2 527 VI.11.13—VI.11.18
Hoelder, E. 119 373 612
Hoermander, L. 1166 1170
Homeomorphism, condition for I.5.8 18
Homeomorphism, definition I.4.15 13
Homomorphism between algebras 40
Homomorphism between Boolean algebras 43—44
Homomorphism between groups 35
Homomorphism between rings 39
Homomorphism, natural, between linear spaces 38
Hopf, E. 669 670 722 728 729 1274
Hopf, H. 47 467
Horn, A. 610 1079
Hotta, J. 466
HS 1010
Hukuhara, M. 474
Hurewicz, W. 467 722 729
Hurwitz, W.A. 462
Hyers, D.H. 92 471 609
Hypergeometric series and equation XIII.8 1509
Ideal(s) in a ring 38
Ideal(s) in an algebra 40
Ideal(s) of operators 552—553 611
Ideal(s), existence of maximal 39
Idempotent element, definition 40
Idempotent operator or projection, definition 37
Imaginary part of a complex number, definition 4
Inaba, M. 474
Independent, linearly 36
Index, definition VII.1.2 556
Indexed set 3
Inequalities, M. Riesz convexity theorem VI.10.11 525
Inequalities, M. Riesz convexity theorem, applications to other inequalities VI.11 526
Inequalities, remarks on 541
Inf A 3
Infimum of a set of real numbers 3
Infimum, limit inferior of a sequence of sets 126
Infimum, limit inferior of a set or sequence of real numbers 4
Infinitesimal generator of a group 627—628
Infinitesimal generator of a semi-group of operators, definition VIII.1.6 619
Infinitesimal generator of a semi-group of operators, functions of VIII.2
Infinitesimal generator of a semi-group of operators, perturbation of VIII.11.19 631
Infinitesimal generator, study of VIII.1
Ingleton, A.W. 88 400
Inner product in a Hilbert space IV.2.26 242
Integrable function, conditions for integrability III.2.22 117 III.3 III.6 IV.8 IV.10.9—IV.10.10
Integrable function, definition III.2.17 112 IV.10.7
Integrable function, properties III.2.18—III.2.22 113—117 IV.10.8
Integrable function, simple function, definition III.2.13 108
Integrable function, simple function, properties III.2.14—III.2.18 108—113
Integral with vector valued measure IV.10.7 323
Integral, change of variables III.10.8 182
Integral, countable additive case III.6
Integral, extension to positive measurable functions 118—119
Integral, finitely additive case III.2—III.3 III.2.17
Integral, integration by parts III.6.22 154
Integral, line integral 225
Integral, summability of IV.13.78—IV.13.101 351—356
Integral, with operator valued measure X.I. 893
Interior mapping principle II.2.1 55
Interior mapping principle, discussion of 83—85
Interior of a set I.4.1 10
Interior point I.4.1 10
Internal point, definition V.1.6 410
Intervals, definitions 4 III.5.15
Invariant measures V.11.22 460 VI.9.38—VI.9.44
Invariant metric in a group 90—91
Invariant metric in a linear space II.1.10 51
Invariant set 3
Invariant subgroup 35
Invariant subspace, definition of X.9 929
Invariant subspace, reducing an operator X.9 929
Inverse function and inverse image 3
Inverse of an operator and adjoints VI.2.7 479
Inverse of an operator and adjoints, existence and continuity of VII.6.1 584
Inverting sequence of polynomials VIII.2.12 650
Involution in a B-algebra IX.1.1 860
Involution in an algebra 40
Ionescu Tulcea, C.T. 926
Irregular singularity of a differential equation XIII.6 1432 1434
Isolated spectral point VII.3.15 571
Isometry, discussion of 91—92
Isometry, embedding of a B-space into its second conjugate space II.3.18—II.3.19 66
Isometry, embedding of a B-space into its second conjugate space, isomorphism and equivalence II.3.17 65
Isomorphism see also "Homomorphism"
Isomorphism, topological see "Homeomorphism"
Iyer, V.G. 399
Izumi, S. 235 382 388 392 543 552
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -finite measure spaces
-finite measure spaces  topology
topology 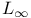
 -measure
-measure