|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Faith C. — Rings and Things and a Fine Array of Twentieth Century Associative Algebra |
|
|
 |
| Предметный указатель |
"Alice-in-Wonderland" 278
"Captain" Bill 318
"Chicago Seven" 321
"Crazy Eddie" 318
"Hagar The Horrible" 301
"Illiac" 281
"Maniac" 280
"Midnight" 276
"Tiger" (Walker) 281
"Tinkers to Evens to Chance" 303
"Tokyo Rose" 306
"Undergraduate Gems at Rutgers" 321—322
"Zebra" 276
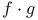 see "Finitely generated" see "Finitely generated"
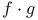 -injective module 4.2Bs 6.Es -injective module 4.2Bs 6.Es
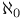 -injective 4.2Bs -injective 4.2Bs
 -injective 3.10A 7.45s -injective 3.10A 7.45s
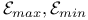 ring 6.38(4) 16.39s ring 6.38(4) 16.39s
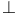 acc (= acc on annihilator left ideals) 1.24A acc (= acc on annihilator left ideals) 1.24A
 -quasi-injective module 3.9 -quasi-injective module 3.9
 -regular ring 8.4Fs -regular ring 8.4Fs
 -cyclic 5.1As -cyclic 5.1As
 -injective module 3.7As 3.14—3.16 7.33—7.34 -injective module 3.7As 3.14—3.16 7.33—7.34
 -pure-injective module 6.55s -pure-injective module 6.55s
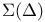 -ring 7.47s -ring 7.47s
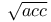 on radical ideals 14.34s on radical ideals 14.34s
 -differential 7.14f -differential 7.14f
(Strongly) invariant coefficient ring 10.1s
Abelian idempotent 4.3As
Abelian von Neumann regular ring (=VNR) 4.3As
Abelian — von Neumann regular ring 4.3As
Abhyankar — Heinzer — Eakin Theorem 10.5
Absolute value 1.30ff
ACC see "Ascending chain condition"
Acc on radical ideals 14.34—14.38
acc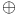 = acc on direct sums 3.13s = acc on direct sums 3.13s
acc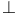 (= acc on annihilator right ideals) 1.24A (= acc on annihilator right ideals) 1.24A
acci (= acc on irreducible ideals) 16.35s
accra (= acc on right annihilator ideals) 2.37G
accsi (= acc on subdirectly irreducible ideals) 16.35s
Adkins, Theodore 255
Affine algebra 14.46
Affine ring (= 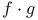 ring) 2.21Bs 2.21Bf ring) 2.21Bs 2.21Bf
Ahsan theorem 12.4C'f
Akasaki theorem 3.29
Akiba theorem 9.24(3)
Al-Huzali — Jain — Lopez-Permouth theorem 6.37
Alamelu theorem 12.23—12.24
Albert 48
Albert theorem 2.50f
Albert, Adrian A. 258—259 286
Albrecht theorem 3.23A—3.23B
Albu 194 211
Albu — Nastasescu theorem 3.33D
Aldosray 44
Algebra Seminar ("World's Greatest") 313
Algebra, affine 14.46
Algebra, algebraic 1.28As
Algebra, free 15.14s 15.14ff
Algebra, polynomial identity (= PI) 15.1s 15.14s
Algebra, separable 14.15Bs
Algebra, split-split 4.15B
Algebraic algebra 1.28As 15.1(7)
Algebraic bounded degree 15.1(7) 15.12
Algebraic function field 1.28As
Algebraic number field 1.28C(2)
Algebraic, absolutely 1.28As 2.40s
Algebraic, matrix 2.6Bs
Algebraically closed field 1.28Bs
Algebraically compact 1.25s 6.Af
Algebraically compact module 1.25s 6.Af
Alliluyeva, Svetlana 271 318
Almost maximal ring 5.4Bs 5.16
Almost maximal valuation ring 5.4D 5.52s
Amdal — Ringdal theorem 5.2C
Amitsur 19 24 36 72 144 176
Amitsur theorem 2.6C 2.40 2.49 3.43—3.49 15.14
Amitsur — Kaplansky Theorem 15.4
Amitsur — Levitzki theorem 15.2
Amitsur — Small Theorem 3.36D 15.17
Amitsur, Shimshon 288—289 304
Anarin 30
Anarin — Zjabko theorem 2.16Cf
Anderson 137 168
Anderson — Fuller theorem 8.6 8.8
Anderson, Frank W. 281
Anh 108 111 127 197
Anh theorem 13.6
Annie Page theorem 9.26E
Annihilator, chain conditions on 3.7A—3.7B 16.19
Annihilator, double condition 3.8
Annihilator, maximal 2.33Es
Annihilator, right ideal 2.16F 2.37Es
Annulet 2.37Es 16.30s
Ara, Pere 309
Arena — Kaplansky theorem 4.19A
Arens 94
Arens — Kaplansky Theorem 4.19A
Arhangel’skii 77 193
Arithmetic ring 6.4
Armendariz 181
Armendariz theorem 6.4
Armendariz — Steinberg Theorem 4.5 4.18
Armstrong, Neil 302
Artin — Schreier theorem 1.30ff
Artin — Tate 3.8s
Artin — Tate Theorem 3.8s
Artin — Wedderburn theorem 2.1ff
Artin, E. 13 21 23 49 57 243
Artin, E. conjecture 2.6ff
Artin, E. problem 2.7s
Artin, E. question 2.7s
Artin, Emil 315 315n 316 319
Artin, Karin 315
Artin, M. 99
Artin, M. theorem 4.14s
Artin, Michael ("Mike") 315 316
Artin, Nataly Jasny 315
Artin, Thomas 315
Artinian modules 2.17As
Artinian rings 2.1f
Asano 151
Asano criterion 5.1A
Asano theorem 5.1A
Ascending chain condition (acc) on right annihilators (acc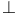 ) 1.24A ) 1.24A
Ascending chain condition (acc) on right ideals 2.2s
Ascending chain condition (acc) on submodules 2.17As
Ascending Loewy chain 3.33As
Asensio 135
Ashbacher, Michael 301
Ass(M), Ass*(M) 16.11 16.17
Atkins 245
Attenborough, Sir Richard 295
Auslander 99 160—161 243 253
Auslander theorem 4.1A 11.9 14.11—14.12 14.15.1
Auslander — Buchsbaum theorem 14.16
Auslander — Goldman theorem 4.13f
Auslander, Maurice ("Moe") 299 315
Automorphism definition 2.5As
Automorphism group 2.7s see
Automorphism group, cleft 17.13As
Automorphism group, dependent 17.0s 17.9ff
Automorphism group, independence theorem 17.0
Automorphism group, quorite 17.9s
Automorphism, inner 2.5A
Ayoub, C. theorem 1.26A
Azumaya 24 49 71 114 157 194
Azumaya algebra 4.13
Azumaya diagram 8.As
Azumaya theorem 4.15 4.20 13.7
| Azumaya — Krull — Schmidt unique decomposition theorem 8As
Babai, L. 290n
Baer 5 45 52 196
Baer criterion 3.2C
Baer lower nil radical 2.38A
Baer theorem 1.18 3.2
Baer, Reinhold 263 284 299 315
Baire category theorem 16.6
Balanced module 3.50Bf 13.29s 13.30As
Balanced rings 13.29s
Balcerzyk theorem 1.19A 1.20A
Ballet theorem 13.11A
Bamberger, Louis 273 278
Barr, Patricia ("Patty") 258
Barrow, John D. 256
Basic indempotent 3.53
Basic module 3.53
Basic ring 3.52
Basis number 1.1 3.63
Basis, countable 1.1
Basis, finite 1.1
Basis, free 1.1
Basis, normal 17.1s
Basis, transcendence 1.28
Bass 61 69 87—88 99 124 215
Bass theorem 2.24 3.4B 3.24A 3.26—3.27 3.30—3.32 3.33C 13.21
Bass, Hyman ("Hy") 287 305
Baxter 48
Beachy 80 102 181
Beachy theorem 3.58—3.61 7.9
Beachy — Blair 6.32A
Beachy — Kamil theorem 3.60
Beck theorem 3.15 3.16 3.28 16.33
Beck — Trosborg theorem 3.79
Becket, Samuel 282
Begin, Menachem 288
Bell 135
Berberian, Sterling ("Sam") 261
Bergman 20 130
Bergman theorem 6.33f 9.26A
Bergman, George 291
Berman 88
Bernstein, Felix 284
Bezout Domain 7.5Bs
Bezout ring 7.5Bs
Bialnicki theorem 1.21 A
Bigelow, Julian 280
Birkenmeier 94 104
Birkhoff 33 240
Birkhoff theorem 2.17C
Birkhoff, Garrett D. 255 291
Birula theorem 1.21A
Bishop, Errett 276
Bjoerk 87 143 184 200 209
Bjoerk theorem 3.5F 3.32f
Blair theorem 6.32A
Blair, Robert ("Bob") 261
Blassenohl, D. 256
Bloustein, Edward J. 302
Blumenthal 23
Bochner, Solomon 317
Bokut’ 132
Bollabas, B. 290n
Bonic, Robert ("Bob") 316—317
Boole 33
Borel 87
Borel, Armand 267—268 270—271 312
Borel, Gaby 270—271
Borho 218
Bounded generator (BG) 8.8ff
Bounded order 1.8 1.14
Bounded ring 5.44Bs 15.17s
Bounded, strongly 5.44s
Bourbaki 85
Bourbaki — Lambek theorem 4.B
Bourbaki, N. 265 313 316
Bowtell 132
Boyle 172
Boyle conjecture 3.9C
Boyle theorem 3.9B 3.18B
Boyle, Ann Koski 286—287
Brandal 111
Brandal theorem 5.6
Brandeis 299
Brando, Marlon 295
Brauer 19 68 78 160 177
Brauer group 2.5Bff 4.16As
Brauer — Auslander — Goldman-group 4.15Af
Brauer — Hasse — Noether theorem 2.5Bff
Brauer, Richard 291 301
Bredon, Glen 299
Brewer 35 72 127 245
Brewer — Rutter Theorem 10.2—10.4
Brewer — Rutter — Watkins 6.12
Brodskii theorem 3.77—3.78
Bronowski, Jacob 300
Browder, Bill 316
Brown 49 94 211
Brown, Karen 299 315
Brown, Mort 275—276
Bruns 205
Buchsbaum, David 299 315
Bumby — Osofsky Theorem 3.3
Bumby, Dick 283—284
Burch 230
Burgess 48
Burnside 18
Burnside theorem 2.4
Busque — Herbera Theorem 4.17A
Busque, Claudi 309
Caesar, Julius 311
Cahen 167
Cailleau 64
Cailleau theorem 3.14
Calaprice, Alice 311n
Caldwell 161
Caldwell, Bill 283
Camillo 70 77—78 141 157 168 242 254
Camillo remarks (letters) §17 Notes
Camillo theorem 1.23 3.33F H 3.51' 4.1B 5.20B 6.60—6.61 13.29 13.30E 16.51
Camillo — Fuller Theorem 4.26 13.30 13.30D
Camillo — Guralnick theorem 9.3
Camillo, Barbara 271
Camillo, Vic 271 286—287 312 319
Camps 124 159—160
Camps — Dicks Theorem 8.D
Camps — Menal Theorem 8.8ff
Camps, Rosa 269 308—309
Camus, Albert 317
Cancellation module 6.3Ds
Cancellation property 6.3Ds
Cancellation, matrix 10.8f (see p.174)
Cantor — Bernstein theorem 3.3
Capson 230
Carleson, Lennart 269
Carr, Raymond 311n
Cartan 52 206
Cartan theorem 2.6 2.7 3.4
Cartan — Brauer — Hua Theorem 2.15As
Cartan — Jacobson Theorem 2.7
Cartan, Henri 262—263
Castellet, Manuel 308
Castelnuovo theorem 1.31A
Cateforis — Sandomierski theorem 4.1E
Category mod-R 3.51s
Category of right R-modules 3.51s
Cauchon 71
Cauchon theorem 3.34A(1)
Cayley 15 21 see
Cedo 133 159 164
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



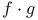
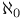 -injective
-injective  -injective
-injective 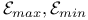 ring
ring 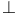 acc (= acc on annihilator left ideals)
acc (= acc on annihilator left ideals)  -quasi-injective module
-quasi-injective module  -regular ring
-regular ring  -cyclic
-cyclic 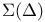 -ring
-ring 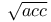 on radical ideals
on radical ideals  -differential
-differential  = acc on direct sums
= acc on direct sums